Mathematics for Construction: Detailed Solutions and Analysis

This document provides a comprehensive solution to a construction mathematics assignment. It covers a range of topics, including calculations for rectangular areas, solving equations related to penalty clauses, and converting units of speed and fuel consumption. The assignment also delves into arithmetic and geometric progressions, logarithmic and hyperbolic equations. Furthermore, the solution includes statistical analysis of data, such as producing histograms, cumulative frequency curves, and extracting measures of central tendency and dispersion. The document also explores normal distribution tests, replacement policies, and hypothesis testing, providing detailed explanations and calculations for each scenario. The solution encompasses various aspects of mathematics relevant to construction projects, offering a thorough understanding of the concepts and their applications. The student provides the assignment to be published on Desklib, a platform offering AI-based study tools.

Mathematics for construction

Table of Contents
TASK 1............................................................................................................................................3
TASK 2............................................................................................................................................9
Scenario 1.........................................................................................................................................9
a. Producing histogram with frequency density.....................................................................9
b. Producing cumulative frequency curve and extracting median and interquartile range. .11
c. Extracting mean, range and standard deviation................................................................13
Scenario 2.......................................................................................................................................13
A.a Normal distribution test.................................................................................................13
A.b Deciding interval allowed for replacement of not more than 10% prior to replacement
Type A..................................................................................................................................13
A.c. Practical consideration for replacement policy.............................................................14
A.d Replacement time affected Type B...............................................................................14
A.e Increment of 25% cost is preferable or not....................................................................15
A.f. Type C..........................................................................................................................15
B Testing hypothesis with 5% level of significance with both two and one tailed test.......15
TASK 3 .........................................................................................................................................18
TASK 4 .........................................................................................................................................22

TASK 1
Question – 1 A building services engineer is to design a water tank for a project. The tank has a
rectangular area of 26.5m2. With the design specifics of the width being 3.2m shorter than the
length, calculate the length and width to 3 significant figures for resource requirements
Ans :
width= 3.2 m
length = 3.2 m
area = 26.5 meter square
area of rectangle= l X b
222 5 = l x 3.2
l= 26.5 / 3.2
l = 8.28
where
width = 3 m
area = l x b
26.5 = lx 3
l= 26.5 / 3
l= 8.83 m

Question – 2 As an employee of company JR construction you have received a letter regarding
the project your company is working on. It has a penalty clause that states the contactor will
forfeit a certain some of money each day for late completion. (i.e. the contractor gets paid the
value of the original contract less any sum forfeit). If she is 5 days late she receives £4250 and if
she is 12 days late she receives £2120. Calculate the daily forfeit and determine the original
contract.
Ans :
Let the original contract amount be x and per day forfeit be y.
When work is delayed by 5 days:
x – 5y = 4250 (1)
Similarly when work is delayed by 12 days:
x – 12y = 2120 (2)
On solving equations 1 and 2 we get
y = 304.28 and
x = 4250 +(5*304.28) = 5771.4
Thus
Daily forfeit = £304.28
Original contract amount = £5771.4
Question – 3 A car driving at an average speed 65 miles/hour
Ans :
A)
1). Average speed= 65 miles/ hour [1 mile = 1760 yards]
65 miles per hour = 65 x 1.609 = 104.585 yard/ second
65 miles per hour = 29.05746 meter per second
2). Time = distance / speed
Time = 100/ 29
Time = 3.44 hour/ second

3). 30 miles / gallon
(miles/100 km ) x (liters/gallon) / (miles/gallon)
(3.785 * 62.14)/30 = 235.19/30 = 7.84 liters/100 km
4). 100 km/ 7.84 liter = 12.755 km per litre
= 7.84 l x 100 /100
= 7. 84 litre for the journey.
B). Formula → Lift =k x ρ x V^2 x A
lift = meter2 x Kg/meter3 x in2
Lift = Kg. m/s2 = newtons or slug
1. An arithmetic sequence is given by b, , , 0....... 3 3 2b b  Determine the sixth term  State
the kth term  If the 20th term has value of 15 find the value of b and the sum of the first 20
terms
Ans :
a). a = a+(n-1)d
a = b(6-1)b/3
a = bx 5b/3
a = 8b/3 6th terms
b). The k term is given by :
a(k) = b + (k-1)* (b/3)
c). a(20)= b +(20-1)*(b/3)
15 = (3b +19b)/3

45= 22b
b= 2.04
Sum of n terms of A.P. = (n/2)*[2a + (n-1)*d]
n = 20 , a= b= 2.04, d =b/3 =0.68
On substituting the values in equation we get
S(20) = 10 * [4.08 + 12.92]
= 170
Thus the sum of first 20 terms of given AP is 170
2. For the following geometric progression 1, ½, 1/4 ........ determine
a) The 20th term of the progression = a(1- r^n) / 1-r
= (1-(1/2)^20) / 1- ½
= 39 x 2 / 40
= 39 / 20
b). Sn = ∑ (n=0) ar^n
Sn = 1/2(1-r^∞) / 1-r
when the value of r is infinity it means the entire system it
Solve the following Equations for x :
(a) 2Log (3x) + Log (18x) = 27
Ans : log ((3x^2)) + log (18x) = 27
log ((3x)^2 . 18X ) = 27
log ((3x)^2 . 18X ) = log (10^27)
(3x)^2.18x = 10^27

Simplify
162x^3 = 10^27
Solve
x= 50000000√4. 3^2/3
(b) 2LOGe(3x) + LOGe(18x) = 9
Ans : log e((3x^2)) + log e(18x)= 9
9log (e)x^2 + 18log(e)x-9 =9-9
Simplify
9log (e)x^2 + 18log(e)x-9 = 0
Use quadratic equation:
x ,  = -b +/- √b^2 – 4ac / 2a
x= -18log (e) + √ 32log(e^2)+324log(e) / 18log (e)
(c) Solve the following Hyperbolic Equations for the variables involved
1. Cosh(X) + Sinh(X) = 5
Ans : Cosh(x)+ -e^-x +e^x /2 = 5
(e^-x +e^x / 2) +(-e^-x+e^x/2) =5
x= In (5)
2. Cosh(2Y) - Sinh(2Y) = 3
Ans : cosh (2y)- (-e^-2y+e^2y/2) = 3
(e^-2y + e^2y / 2) - (-e^-2y+e^2y / 2) = 3
simplify
e^-2 +e^2y- (-e^-2y +e^2y)= 6
(e^y)^{-2}+(e^y)^2-(-(e^y)^{-2}+(e^y)^2)=6
(u)^{-2}+(u)^2-(-(u)^{-2}+(u)^2)=6

u= √1/3, u = -√1/3
e^y = √1/3 : y = -1/2 In (3)
3. Cosh(K) * Sinh(K) = 2
Ans : cosh(k){-e^{-k}+e^k}{2}=2
{e^{-k}+e^k}{2} . {-e^{-k}+e^k}{2}=2
Multiply both side
{e^{-k}+e^k}{2]}. {-e^{-k}+e^k}{2} . 4=2. 4
Simplify
(e^{-k}+e^k)(e^k-e^{-k}) = 8
(u)^{-1}+u) (u-(u)^{-1})=8
u = √4+√17 , u= -√4+√17
putting u = e^k solve the following in order to find k
k = 1/2In(4+√17)
4. Cosh(M) / Sinh(M) = 2
Ans:
f{cosh (m)} / {-e^{-m}+e^m}{2}}=2
{e^{-m}+e^m}{2}} / {-e^{-m}+e^m}{2}}=2
Simplify
{e^{-m}+e^m}{2} = -e^{-m}+e^m
(e^m)^{-1}+e^m}{2}=-(e^m)^{-1}+e^m
(u)^{-1}+u}{2} = -(u^{-1}+u
u = √3, u= -√3

e^m = √3 : m= 1/2In(3)
e^m = -√3
m= ½ In (3)
TASK 2
Scenario 1
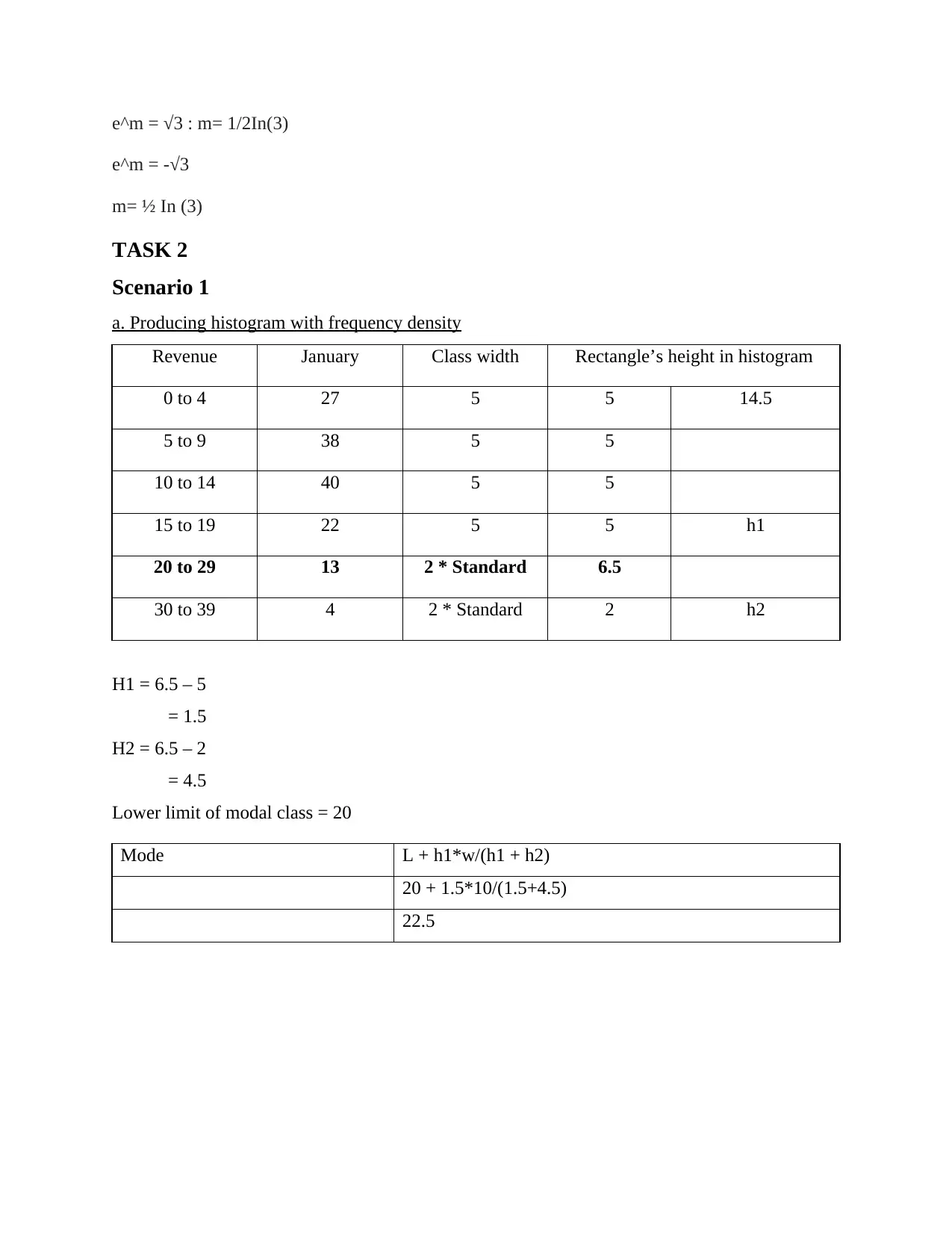
a. Producing histogram with frequency density
Revenue January Class width Rectangle’s height in histogram
0 to 4 27 5 5 14.5
5 to 9 38 5 5
10 to 14 40 5 5
15 to 19 22 5 5 h1
20 to 29 13 2 * Standard 6.5
30 to 39 4 2 * Standard 2 h2
H1 = 6.5 – 5
= 1.5
H2 = 6.5 – 2
= 4.5
Lower limit of modal class = 20
Mode L + h1*w/(h1 + h2)
20 + 1.5*10/(1.5+4.5)
22.5

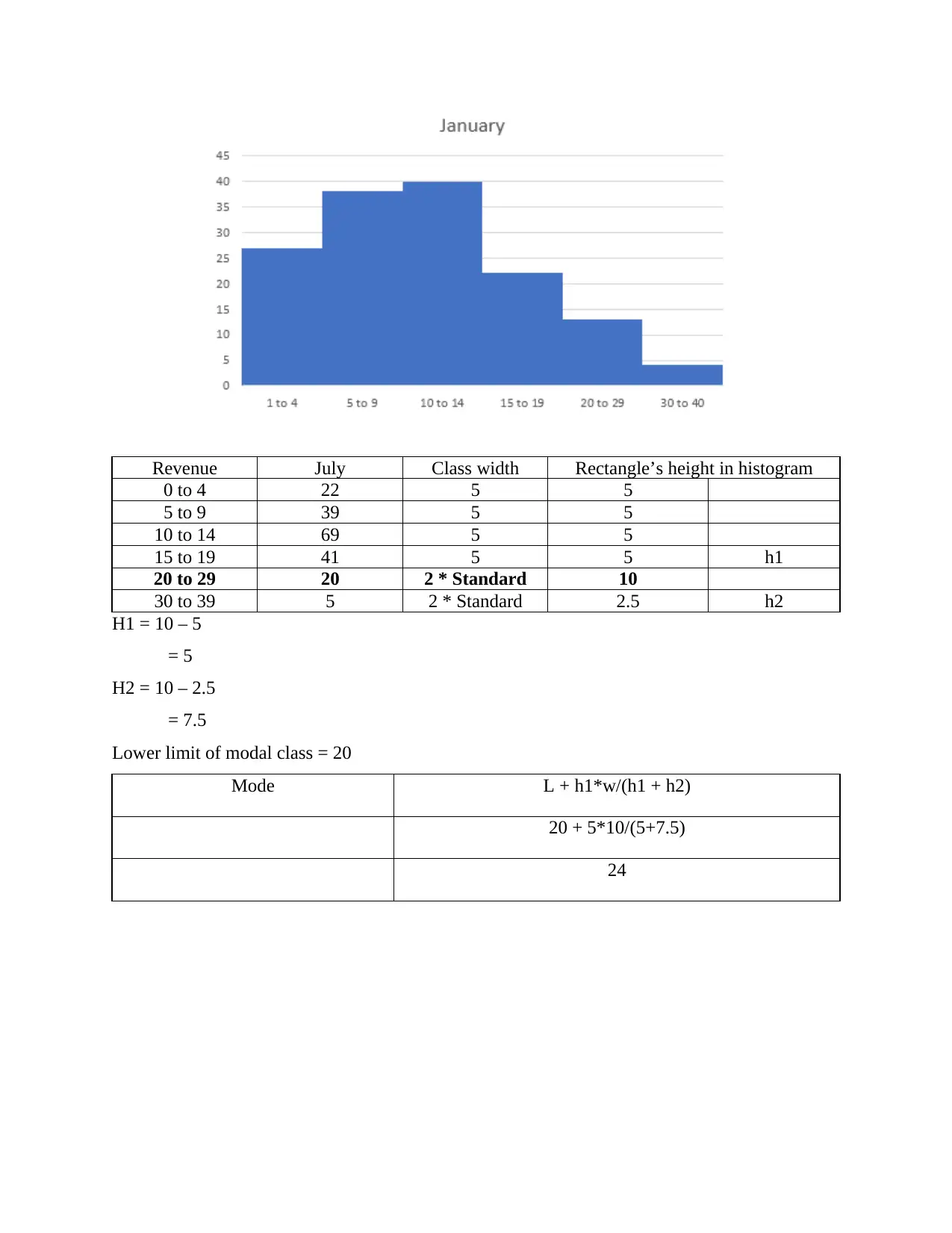
Revenue July Class width Rectangle’s height in histogram
0 to 4 22 5 5
5 to 9 39 5 5
10 to 14 69 5 5
15 to 19 41 5 5 h1
20 to 29 20 2 * Standard 10
30 to 39 5 2 * Standard 2.5 h2
H1 = 10 – 5
= 5
H2 = 10 – 2.5
= 7.5
Lower limit of modal class = 20
Mode L + h1*w/(h1 + h2)
20 + 5*10/(5+7.5)
24

b. Producing cumulative frequency curve and extracting median and interquartile range

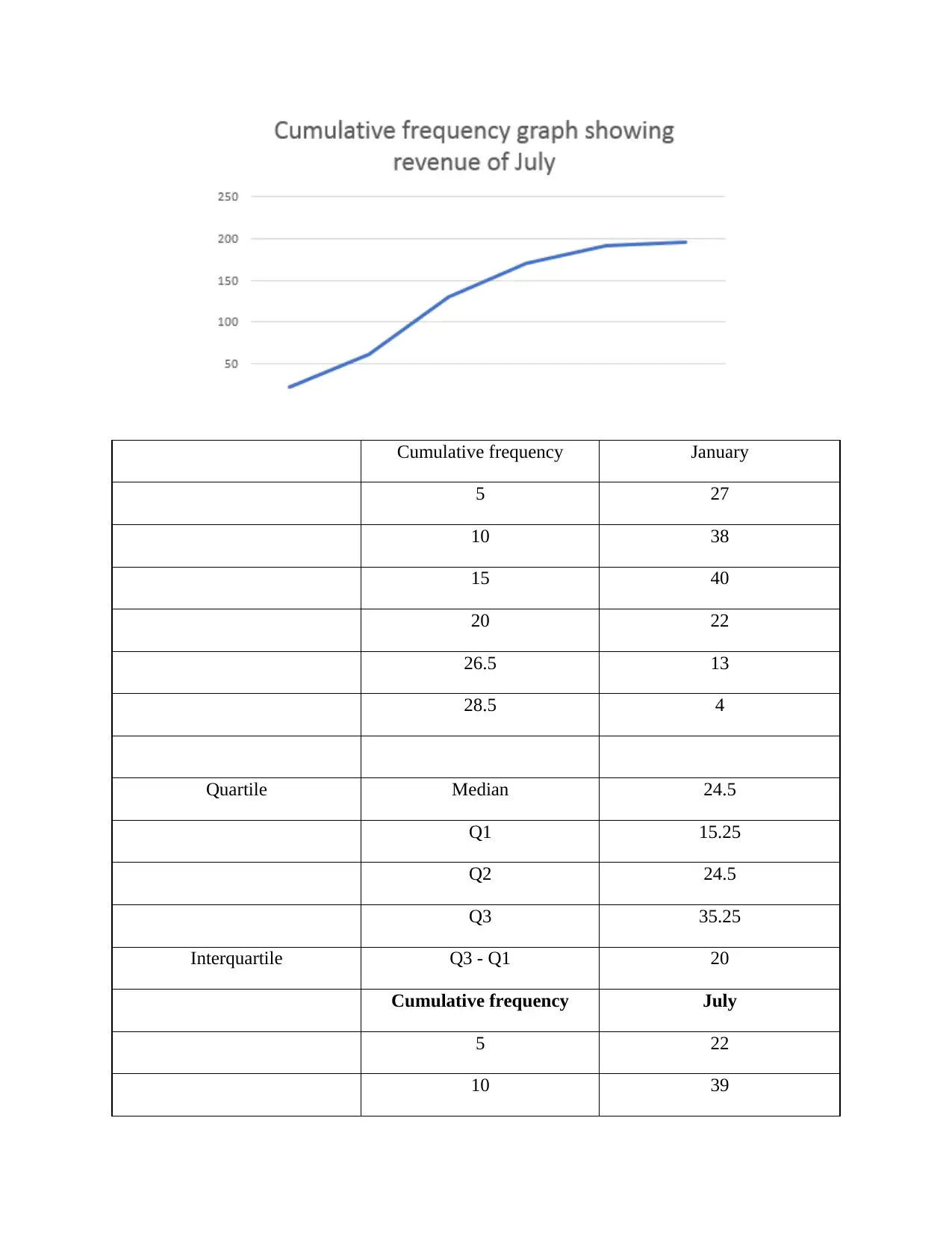
Cumulative frequency January
5 27
10 38
15 40
20 22
26.5 13
28.5 4
Quartile Median 24.5
Q1 15.25
Q2 24.5
Q3 35.25
Interquartile Q3 - Q1 20
Cumulative frequency July
5 22
10 39