Math Assignment: Powers, Roots, Linear Equations, and Data Analysis

This homework assignment presents solutions to a range of mathematical problems. The assignment begins with questions on powers and roots, including simplification and calculations involving exponents. It then moves on to solving linear equations, inequalities, and finding the intersection of lines. The assignment also covers statistical concepts, such as calculating slopes, y-intercepts, and interpreting data through histograms and scatter plots. Furthermore, it delves into probability, including calculating probabilities of events and applying the concept of net present value (NPV) in financial scenarios. The solutions are presented with clear steps and explanations, demonstrating the application of mathematical principles to solve each problem.

Question 1
(a) The a, b, c and d range [2-25]
(b) Single power of a
¿ ab ×ac
ad = a15 × a7
a20 = a15+7
a20 = a22
a20 =a22−20=a2
(c) 3
√a × 3
√b
¿ 3
√ a × 3
√b=3
√10× 3
√15
¿ 3
√ 10∗15=3
√ 150=3
√ 6 . 5
2
3
(d) (b¿ ¿ a)c × bd ¿
(b¿ ¿ a)c × bd =(15¿¿ 10)7 ×1520=(15¿¿ 10∗7)∗×1520 ¿ ¿ ¿
¿ 1570 × 1520=1570+ 20=1590
Question 2
(a) 6−2
(b) 5.6∗10−2
In decimal forms
1
Number a 10
Number b 15
Number c 7
Number d 20

6−2= 1
62 = 1
36 =0.02778
5.6∗10−2= 5.6∗1
102 = 5.6
100 =0.056
It can be seen that 0.056> 0.02778∧hence ,can be said that 5.6∗10−2is bigger.
Question 3
(a) 8( 2t – 4 )=3 t – 6
16 t−32=3 t−6
16 t−3 t=−6+32
13 t=26
t= 26
13 =2
t=2
(b) Given inequality
−4 ≤ x <1
Integer values of x = -4, -3, -2, -1, 0
(c) The two lines would be parallel when their slopes are same.
Let the slope of line 1 is m1 and of line 2 is m2.
Line 1
−6 x=− y −2
y +2=6 x
y = 6x – 2
Compare with y=m1 x +c
2

Slopem 1=6
Now,
Line 2
2 y=6 x +2
y=3 x +1
Compare with y=m2 x+c
Slope m 2=3
It can be seen that m1≠ m2 and thus, the lines are not parallel.
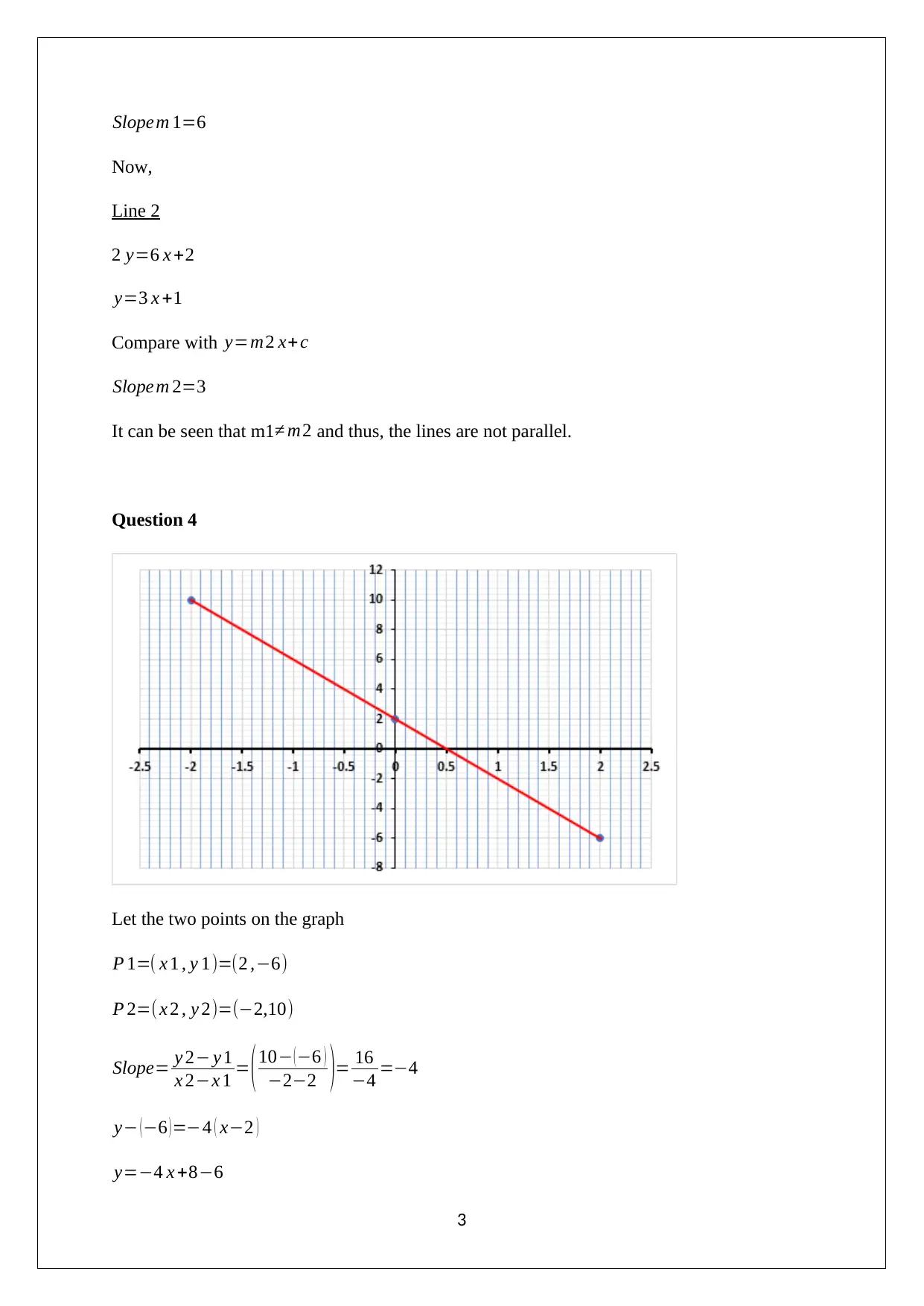
Question 4
Let the two points on the graph
P 1=( x 1 , y 1)=(2 ,−6)
P 2=(x 2 , y 2)=(−2,10)
Slope= y 2− y 1
x 2−x 1 = ( 10− ( −6 )
−2−2 )= 16
−4 =−4
y− (−6 )=−4 ( x−2 )
y=−4 x +8−6
3

y=−4 x +2
Equation y=mx+c
Intercept = +2
Now, linear equation
y=−4 x−2
Therefore, option a is correct.
Question 5
(a) Output = 250 toys
Factory holds = 1000
Order received = 4500
Linear equation and slope and y – intercept
Linear equation T =250 d +1000
Where,
T =Number of toys
d=Number of days
After comparing this with y=mx+c
Slope = 250
Y - Intercept = 1000
(a) Let there is d number of days.
Number of toys after d days = 250 d
Now,
450 0=250 d +1000
4

4500−1000=250 d
3500=250 d
d= 3500
250 =14 day s
Therefore, factory would take 14 days to fulfil this order.
Question 6
(a) Tally of data with 5 classes
Daily caloric intake of women
(Classes)
Tally
400 to 1900 |||| |||| ||
1900 to 2300 |||| ||
2300 to 2700 ||||
2700 to 3100 ||||
3100 to 3500 |
(b) Histogram
Daily caloric intake of women
(Classes)
Frequency
400 to 1900 12
1900 to 2300 7
2300 to 2700 5
2700 to 3100 5
3100 to 3500 1
5

400 to 1900 1900 to 2300 2300 to 2700 2700 to 3100 3100 to 3500
0
2
4
6
8
10
12
14
Histogram
Daily caloric intake of women
Frequency
(c) It is apparent from the histogram that the data is not normally distributed because the
histogram has long right ward tail which implies that data has positive skew.
Question 7
(a) Slope
Let the two points on the graph
P 1=( x 1 , y 1)=(2 , 1117)
P 2=( x 2 , y 2)=(4.5 , 799.5)
Slope= y 2− y 1
x 2−x 1 = (799.5−1117
4.5−2 )=−317.5
2.5
Slope=−127
(b) Y – intercept
y−111 7=−127 ( x−2 )
y=−127 x +254 +1117
y=−127 x +1371
Thus, Y – intercept = 1371
6

(c) Linear equation
Equation y=mx+c
y=−127 x +1371
(d) Rent price =?
Distance from city centre = 5.5 km
y=−127 x +1371
y=(−127∗5.5)+1371
y=672.5
Therefore, the monthly rent would be £672.5.
(e) It is apparent from scatter plot and linear equation with negative slope that variable
distance from city centre and monthly rent are negatively correlated. It means as the
distance from the city increases then the monthly rent would be decreased.
Question 8
(a) Net present value (NPV)
NPV = Total case inflows - Total case outflows
Discount rate = 5%p.a.
Years = 4
NPV = {( 2200
1.051 + 1900
1.052 + 3900
1.053 + 1700
1.054 ) }−8000
NPV =8586.155−8000=£ 586.1 5
(b) NPV of investment comes out to be positive and thus, the owner of the company should
make the investment in the project of buying the new kitchen equipment. Thus, it would
be profitable for the owner to buy machine.
7

Question 9
(a) Number of lottery ticket = 230
Winning tickets = 60
Let the winnings tickets that should be added to box to increase picking a winning ticket
to 0.5 is x.
P ( winningticket ) = n
230 =0.5
n=230∗0.5= 230
2 (for 0.5 probability there should be half of the total tickets of winning
tickets)
Total tickets = 230 + x
Winning tickets = 60+x
For getting a probability of 0.5 total tickets in this case would be (230+x)/2
Hence, 60+ x= 230+ x
2
120+2 x=230+x
x=230−120=110
Therefore, 110 winnings tickets should be added to box to increase picking a winning
ticket to 0.5.
(b) Probability of selecting a king from 52 cards
In 52 cards, there are 4 kings i.e. 1 heart, 1 club, 1 spade, 1 diamond.
P ( king )= 4
52 =0.0769
(c) Box has 4 red and 6 blue balls
P(two balls of same colour) without replacement = ?
Total balls = 4+6 = 10
8

P ( 2red balls ) without replacement =
4
10∗3
4 =0.133
Now,
P ( 2blue balls ) without replacement =
6
10∗5
9 =0.333
P(two balls of same colour) without replacement = 0.133 + 0.333 = 0.466
Task 2
Line 1: y=3 x−6
Line 2: y=3 x +2
Intersection point
3 x−6=3 x+2
−6 ≠ 2
It implies that the lines do not have any intersection point because they do not intersect.
Further, the same slope implies that they are parallel line.
9