Mathematics Homework Solution: Advanced Topics and Problems
VerifiedAdded on 2022/09/09
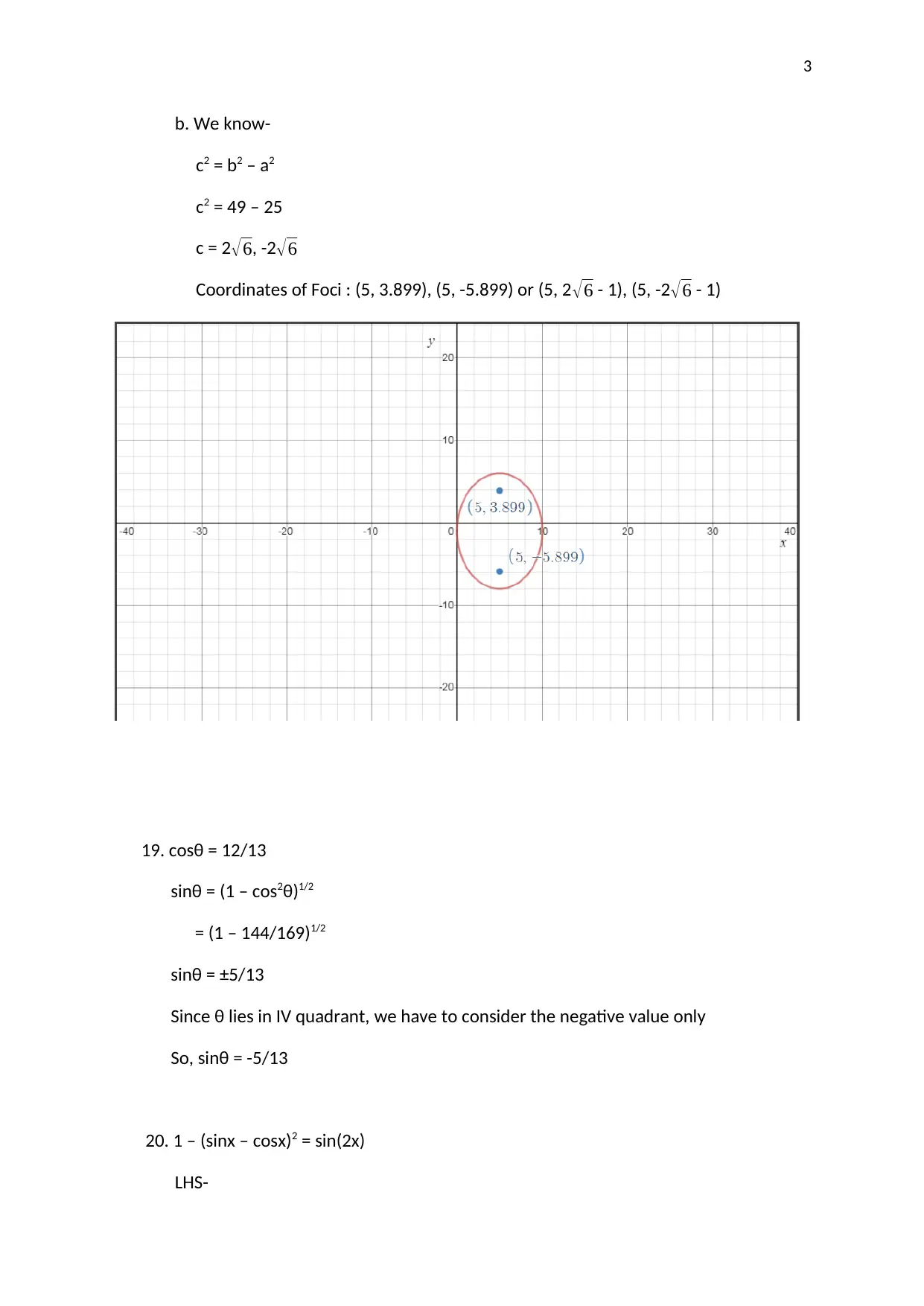
|6
|716
|11
Homework Assignment
AI Summary
This document contains the solutions to a comprehensive mathematics homework assignment covering a wide range of topics. The solutions include answers to multiple-choice questions, detailed step-by-step solutions to problems involving trigonometry (like finding angles and using sine rule), vectors (including vector operations and finding angles between vectors), and algebra (solving systems of equations and working with sequences). The assignment also addresses calculus concepts, such as finding the sum of geometric sequences, and includes solutions to problems involving conic sections (ellipses and parabolas) and polar coordinates. Furthermore, the solutions incorporate real-world applications, such as a word problem involving ticket sales, and proofs of trigonometric identities. The reference list includes a textbook on mathematical methods for physicists and a mathematics textbook.
1 out of 6








![[object Object]](/_next/static/media/star-bottom.7253800d.svg)