Foundations of Mathematics: Week 1 Homework Assignment - Fall 2019

This document presents solutions to a week 1 math homework assignment, covering a range of mathematical concepts. The solutions address problems related to Polya's four-step problem-solving process, geometric and arithmetic series, and calculations of series sums. It also includes solutions to problems involving arithmetic sequences, and reasoning (inductive and deductive). Furthermore, the assignment tackles word problems involving linear equations, and calculations of combinations. The document also addresses problems requiring the application of mathematical formulas to find the number of dots in patterns and the minimum number of steps required to solve practical problems. The solutions are presented with clear explanations and step-by-step calculations to facilitate understanding.

Week 1 HW Assignment – Fall 2019
Name:

Answer 1
Polya’s four-step problem solving process as below
Step- 1 Understand the problem: Understand means clarify the problem. When a problem is
red all the data and components has to be properly cheek.
Step- 2 Devise a plan: Device a plan means that when a problem has been gone to solve,
firstly the equation has to be set then drawing a diagram or chart and solve the problem.
Step- 3 Carry out the plan: In this step, when an equation has been solved then it has to go
with devise plan step. If this a linear equation then before the solving go back and review the
concept.
Step -4 Look back: It means that cheek and interpreted the result.
Answer 2
(a) Given First term (a) = 1
5
1= 25
5
r = 5
It is a geometric series.
T n= arn−1
Or T 1 0= 1*510−1
= 59
(b) It is neither arithmetic nor geometric series.
(c) It is an arithmetic series.
Where (a) = 24
d = 24-21
= 3
T n=a+ (n-1)*d
T 1 0=24+ (10-1)*3
= 51
Answer 3
Given that
a = 132
l = 1780
T n=a+ (n-1)*d
Or 1780 = 132+ (n-1)*1
Or n = 1649

Now
Sn = n
2 (a+l)
= 1649
2 (132+1780)
Sn= 1576444
Answer 4
The number of dots in the 50th figure = 4*49
= 196
It has been seen that number of dots in the first figure = 1
The number of dots in the second figure = 5
The number of dots in the third figure = 13
The number of dots in the fourth figure = 25
So 5-1 = 4, 13-5= 8, 25-13= 12. Their result is multiplier of 4. That means first result
is 1, second is 4*1, third result is 4*2, fourth result is 4*3, ……50th result is 4*49.
Answer 5
Given that the common ratio of a geometric sequence = 4
If each term of the sequence is multiplied by 3, then the common ratio does not change. It’s
still at 4.
Answer 6
6+7 = 13
7+8 = 15
3+4+5= 12
4+5+6 = 15
Counter 2+3= 5
2+3+4 = 9
Answer 7
The next number in the series = 136
1 4 13 34 73 136
3 9 21 39 63
6 12 18 24
6 6 6

Answer 8
It is inductive as well as deductive reasoning. Because Galileo takes this step fpr
experiment.
Theory Prediction Experiment Observation Generalization
Paradigm
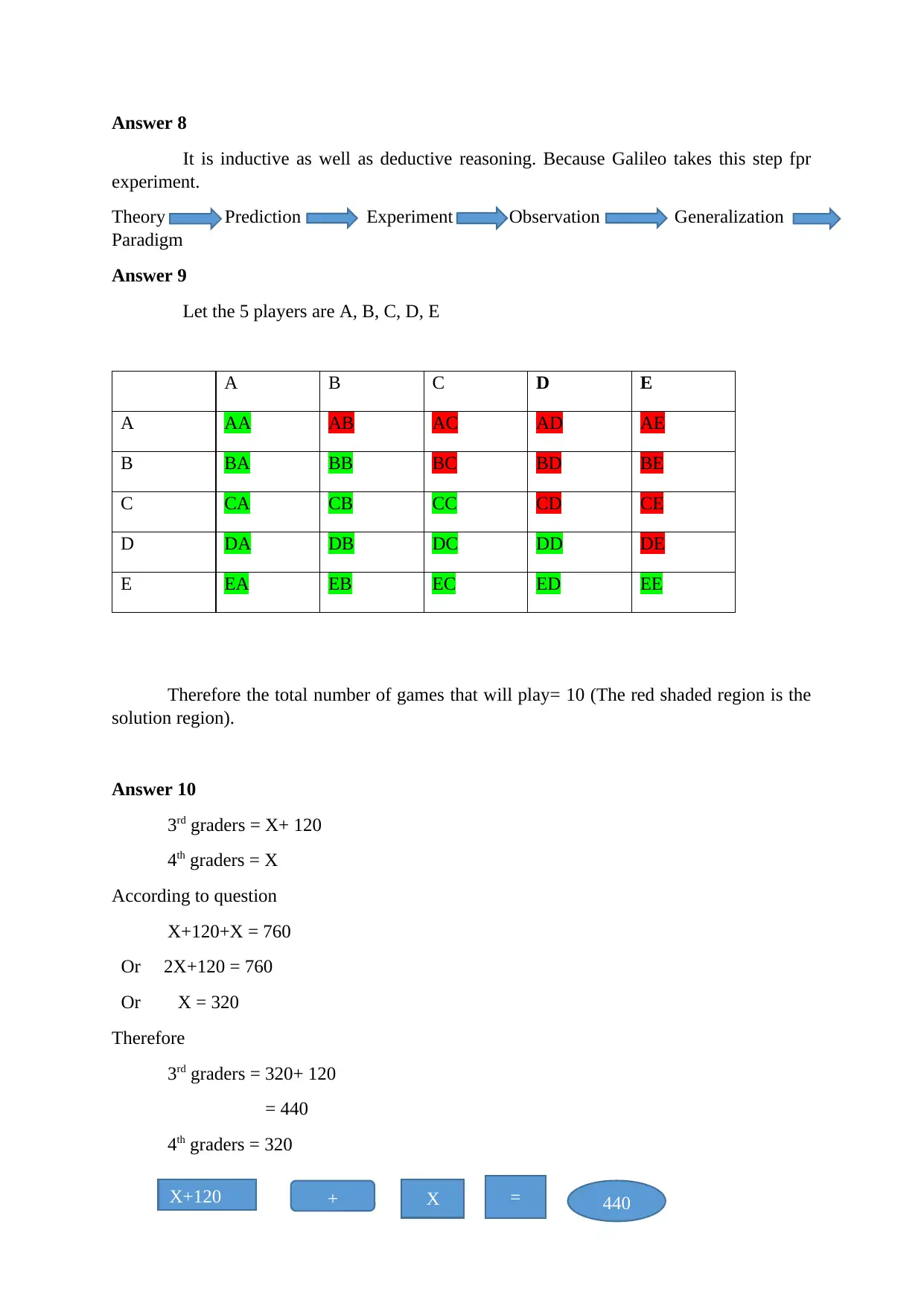
Answer 9
Let the 5 players are A, B, C, D, E
A B C D E
A AA AB AC AD AE
B BA BB BC BD BE
C CA CB CC CD CE
D DA DB DC DD DE
E EA EB EC ED EE
Therefore the total number of games that will play= 10 (The red shaded region is the
solution region).
Answer 10
3rd graders = X+ 120
4th graders = X
According to question
X+120+X = 760
Or 2X+120 = 760
Or X = 320
Therefore
3rd graders = 320+ 120
= 440
4th graders = 320
X+120 + X = 440

Answer 11
Full Cup = X
Half cup = Y
X+Y = 57 …………….. (1)
X*0.50+ Y*0.25 = 23 ……… (2)
0.50 ×equation (1) = 0.50X+Y = 57 ……. (3)
(3) – (2) = 0.75Y = 34
Or Y = 45.33
X = 11.67
Sl. no Half Full Total
1 0.25 0.50 0.75
2 0.25 0.50 0.75
3 0.25 0.50 0.75
4 0.25 0.50 0.75
5 0.25 0.50 0.75
6 0.25 0.50 0.75
7 0.25 0.50 0.75
8 0.25 0.50 0.75
9 0.25 0.50 0.75
10 0.25 0.50 0.75
11 0.25 0.50 0.75
12 0.25 0.50 0.75
13 0.25 0.50 0.75
14 0.25 0.50 0.75
15 0.25 0.50 0.75
16 0.25 0.50 0.75
17 0.25 0.50 0.75
18 0.25 0.50 0.75
19 0.25 0.50 0.75
20 0.25 0.50 0.75
21 0.25 0.50 0.75
22 0.25 0.50 0.75
23 0.25 0.50 0.75
24 0.25 0.50 0.75
25 0.25 0.50 0.75
26 0.25 0.50 0.75
27 0.25 0.50 0.75
28 0.25 0.50 0.75
3Rd grade + 4th
grade =
=
440

29 0.25 0.50 0.75
30 0.25 0.50 0.75
31 0.25 0.50 0.75
32 0.25 0.50 0.75
33 0.25 0.50 0.75
34 0.25 0.50 0.75
35 0.25 0.50 0.75
36 0.25 0.50 0.75
37 0.25 0.50 0.75
38 0.25 0.50 0.75
39 0.25 0.50 0.75
40 0.25 0.50 0.75
41 0.25 0.50 0.75
42 0.25 0.50 0.75
43 0.25 0.50 0.75
44 0.25 0.50 0.75
45 0.25 0.50 0.75
46 0.25 0.50 0.75
47 0.25 0.50 0.75
48 0.25 0.50 0.75
49 0.25 0.50 0.75
50 0.25 0.50 0.75
51 0.25 0.50 0.75
52 0.25 0.50 0.75
53 0.25 0.50 0.75
54 0.25 0.50 0.75
55 0.25 0.50 0.75
56 0.25 0.50 0.75
57 0.25 0.50 0.75
Answer 12
a = 1
d =3
T n=a+ (n-1)*d
T 85=1+ (85-1)* 3
= 253
It is an arithmetic series. Because their common difference is equal.
Answer 13
The number of men = 2
The number of boy = 2
The canoe can carry two boys or one man.

The minimum number of times = 3
Let,
First time Canoe can carry = 2 Boy
Second time Canoe carry = 1 Man
Third time Canoe carry = 1Man
Answer 14
The length of the fence= 400 foot
The distance between the centers of two adjacent posts = 8 feet
Given that the fence begins and ends with a post.
The required number of post = 400/8
= 50
The 50th post will be included at the end. Additionally one post will be required at the
beginning. Since the first post placed at 8 feet from the start.
Therefore the required solution = 50+1
= 51