Mathematics I: Numbers, Sets, and Functions - Homework Problems

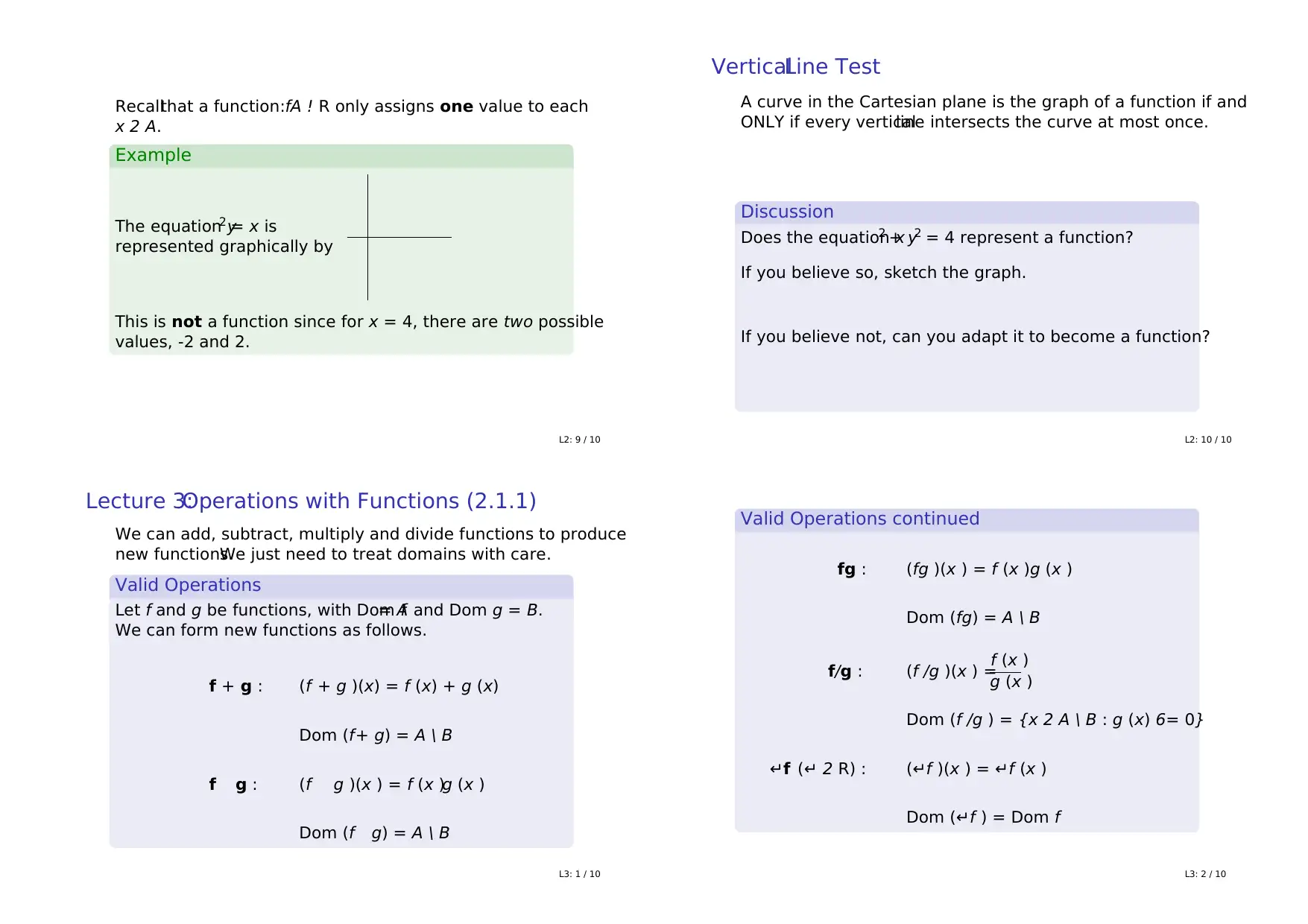
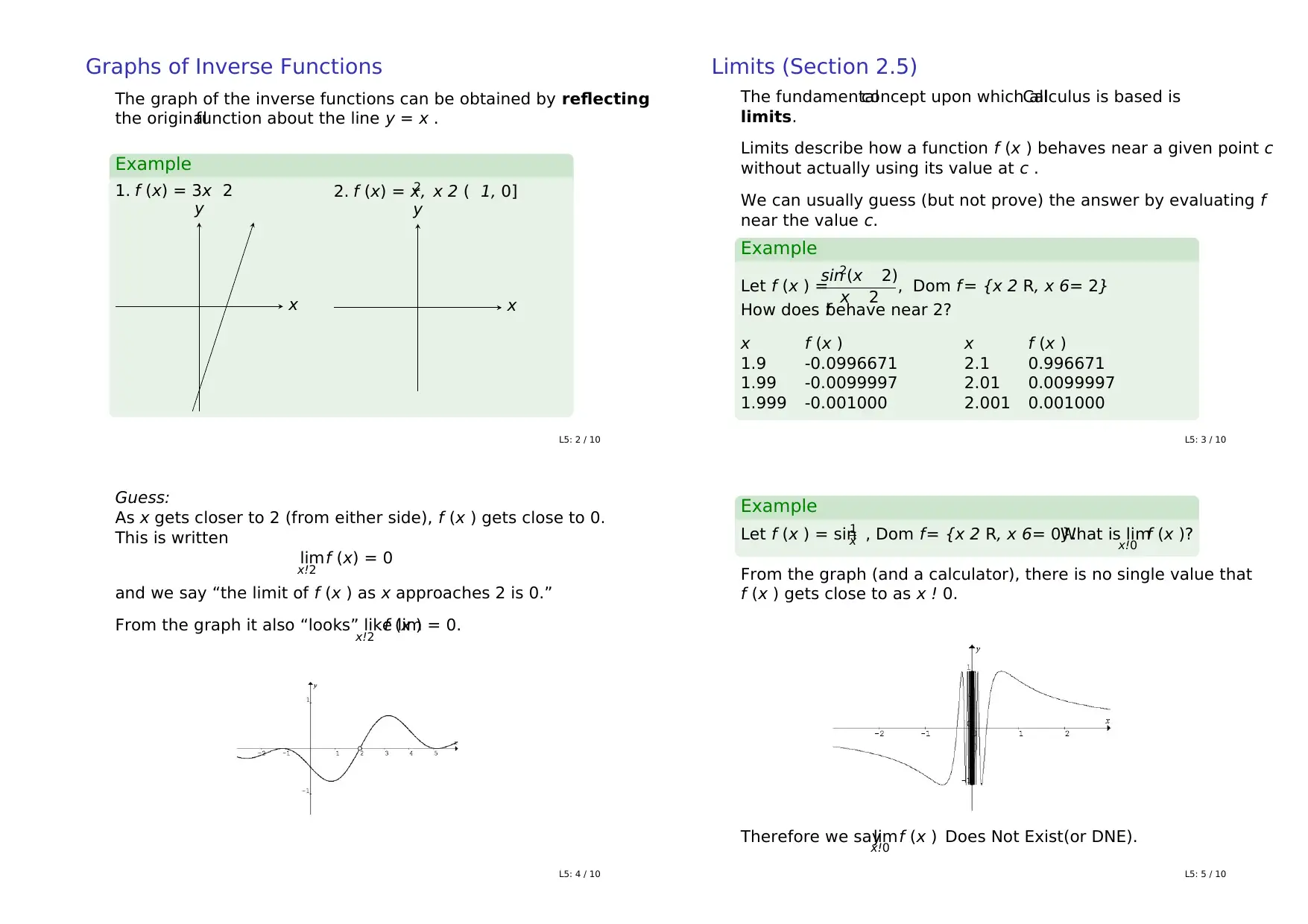
This homework assignment covers fundamental concepts in mathematics, including numbers, sets, and functions. The assignment begins with definitions and notations related to sets, including elements, subsets, and set operations like intersection and union. It then delves into standard sets such as natural numbers, integers, rational numbers, irrational numbers, and real numbers, along with their notations and relationships. The concept of absolute value and interval notation are also explained. The second part of the assignment focuses on functions, defining them as rules that assign a unique output to each input in their domain. It covers common functions like constant, linear, and polynomial functions, and discusses the domain and range of functions. The document also explores function operations such as addition, subtraction, multiplication, division, and composition, along with their respective domains. Furthermore, the assignment introduces the concept of one-to-one functions and methods for decomposing complex functions into simpler ones. The solutions provided offer detailed explanations and examples to aid in understanding these core mathematical principles.

Lecture 1:Numbers & Sets
A set is a collection of things (usually numbers).
Definition (Formalnotation)
A = {x : x satisfies some condition(s)}
Example
A = {x : x is an even number}
B = {x : x is realand 1 < x < 2}
Sometimes we can list the elements.
Example
C = {2, 3, 5, 7, 11, 13}a finite set
D = {2, 3, 5, 7, 11, 13, ...}

Some other notation we adopt:
Z+ - The set of non-negative Integers
Z+ = {0, 1, 2, 3, 4, ...} = {0} [ N
R+ - The set of non-negative Reals
R+ = {x 2 R : x 0}
We can use intervalnotation for continuous sets of realnumbers.
Example
1. {x 2 R : 1 x < 5} = [1, 5)
2. {x 2 R : x <

Lecture 2:Functions (Section 2)
Definition
A function f is a rule or procedure which, for each number x in
some subset A of R, assigns one and only one number f (x) in R.
L2: 1 / 10
Exercise
Let f (x ) =
p x2 4
(a) Evaluate
f (10)
f ( 3)
f (t2)
f (x + 2)
(b) Are there any values of x 2 R for which fis invalid?
L2: 2 / 10
Common functions
f (x) = c Constant function
f (x) = mx + b, m 6= 0 Linear function
f (x) = x Identity function
f (x) = a0 + a1x + a2x2 + ... + anxn Polynomialfunction
of degree n
Question Does x2 + y2 = a2 represent a common function?
L2: 3 / 10
Notation
f : A ! R

Example
1. Let g : R ! R be given by g (x) = x2.
Dom g =
Range g =
2. Let f1 : Z ! R be given by f1(n) = 2n 1.
Dom f1 =
Range f1 =
L2: 5 / 10
There are two parts to a function, the domain and the rule.
Changing the rule or the domain changes the function.
Example
Let f2 :

Recallthat a function f: A ! R only assigns one value to each
x 2 A.
Example
The equation y2 = x is
represented graphically by
This is not a function since for x = 4, there are two possible
values, -2 and 2.
L2: 9 / 10
VerticalLine Test
A curve in the Cartesian plane is the graph of a function if and
ONLY if every verticalline intersects the curve at most once.
Discussion
Does the equation x2 + y2 = 4 represent a function?
If you believe so, sketch the graph.
If you believe not, can you adapt it to become a function?
L2: 10 / 10
Lecture 3:Operations with Functions (2.1.1)
We can add, subtract, multiply and divide functions to produce
new functions.We just need to treat domains with care.
Valid Operations
Let f and g be functions, with Dom f= A and Dom g = B.
We can form new functions as follows.
f + g : (f + g )(x) = f (x) + g (x)
Dom (f+ g) = A \ B
f g : (f g )(x ) = f (x )g (x )
Dom (f g) = A \ B
L3: 1 / 10
Valid Operations continued
fg : (fg )(x ) = f

Exercise
Let f (x ) = (x 1)2 and g (x) = 1
x + 2
.
Dom f = Dom g =
1. (f + g )(x) =
Dom (f+ g) =
2. (fg )(x ) =
Dom (fg) =
3. (f /g )(x ) =
Dom (f /g ) =
L3: 3 / 10
Exercise (continued)
Let f (x ) = (x 1)2 and g (x) = 1
x + 2
.
Dom f = Dom g =
4. (g /f )(x ) =
Dom (g /f ) =
L3: 4 / 10
Discussion
Let f (x) = x(x + 1) and g (x) =
1
x. Find f
g and Dom
⇣f
g
⌘
.
L3: 5 / 10
Composition of Functions
Definition
If f and

Example
Let f (x) = x + 1 and g (x) = x2. Both have domain R.
(f g )(x ) = f (g (x )) Dom (f g) =
= f (x 2)
= x 2 + 1
(g f )(x ) = g (f (x )) Dom (g f ) =

Lecture 4:Decomposition of Functions
Given a complicated function, it can be usefulto break it up as the
composition of severalsimple functions (especially in
di↵erentiation and integration).
Example
1. h(x) = (x 3)4
Let f (x ) = g (x) =
Then h(x) = (f g )(x ).
2. Given g (x ) = sin x , find a fsuch that (f g )(x) = cos2 x .
L4: 1 / 11
Exercise
For each function h(x ), find fand g

Algebraic Test for 1-1
To see if fis 1-1, we let f (a) = f (b) and show that a = b.
Example
1. f (x) = 3x + 2
2. g (x) = 3x2 + 5x 1
L4: 5 / 11
GraphicalTest for 1-1:The HorizontalLine Test
A function fis 1-1 if and ONLY if every horizontalline in the
Cartesian plane intersects the graph of fat most once.
Example
1. f (x) = x3 + 2
2. g (x) = 3x2 + 5x 1
L4: 6 / 11
Exercise
Which of the following functions are 1-1?
1. y = 5x + 1
2. y = cos x
3. y = 2 x3
4. y = x1/3
L4: 7 / 11
Inverse Functions
Exercise
For each pair of functions, find fg and g f .
1. f (x) = x3, g (x) = x1/3
2. f (x) = ex, g (x) = ln x
3. f (x) = 2x 3, g (x) =x + 3
2
L4: 8 / 11

Definition
If f : X ! R is a 1-1 function with Range Y , then there exists an
inverse functionf 1 : Y ! R, with Range X such that
for allx 2 X , (f 1 f )(x ) = x and
for ally 2 Y , (f f 1)(y ) = y .
Example
1. f (x) = x3, f 1(x) = x1/3
2. f (x) = ex, f 1(x) = ln x
3. f (x) = 2x 3, f 1(x) = x + 3
2
L4: 9 / 11
Notes:
1 f 1 6=
1
f !!!
2 If f is not 1-1, it does not have an inverse.
You should always check this first.
3 Dom f 1 = Range f
Range f 1 = Dom f
This can be helpfulto know when finding Range

Graphs of Inverse Functions
The graph of the inverse functions can be obtained by reflecting
the originalfunction about the line y = x .
Example
1. f (x) = 3x 2
y
x
2. f (x) = x2, x 2 ( 1, 0]
y
x
L5: 2 / 10
Limits (Section 2.5)
The fundamentalconcept upon which allCalculus is based is
limits.
Limits describe how a function f (x ) behaves near a given point c
without actually using its value at c .
We can usually guess (but not prove) the answer by evaluating f
near the value c.
Example
Let f (x ) =
sin2(x 2)
x 2 , Dom f = {x 2 R, x 6= 2}
How does fbehave near 2?
x f (x ) x f (x )
1.9 -0.0996671 2.1 0.996671
1.99 -0.0099997 2.01 0.0099997
1.999 -0.001000 2.001 0.001000
L5: 3 / 10
Guess:
As x gets closer to 2 (from either side), f (x ) gets close to 0.
This is written
lim
x!2 f (x) = 0
and we say “the limit of f (x ) as x approaches 2 is 0.”
From the graph it also “looks” like lim
x!2 f (x ) = 0.
L5: 4 / 10
Example
Let f (x ) = sin1
x , Dom f= {x 2 R, x 6= 0}.What is lim
x!0 f (x )?
From the graph (and a calculator), there is no single value that
f (x ) gets close to as x ! 0.
Therefore we saylim
x!0 f (x ) Does Not Exist(or DNE).
L5: 5 / 10

InformalDefinition
Let f be a function and let c be a given point.We say
lim
x!c f (x) = L
if we can ensure that f (x ) is as close to L as we like by taking
values of x close enough to c.
A more formaldefinition can be found on page 2-16 of Section 2.
Geometrically the idea is as follows:
L5: 6 / 10
Notes:
It is not necessary for c 2 Dom f , that is, f (c) need not be