Mathematics 1 TMA 02 Assignment: Comprehensive Math Problem Solutions

This document presents a detailed solution set for a Mathematics 1 TMA 02 assignment. The solutions cover a range of mathematical concepts, including solving inequalities, analyzing functions (including transformations and inverse functions), and applying trigonometric principles. The assignment also involves calculations related to vectors, including component forms and resultant velocities, as well as the application of geometric formulas. The solutions demonstrate step-by-step approaches, including the use of sign analysis charts, trigonometric identities, and geometric formulas. Furthermore, the assignment includes mathematical communication, emphasizing the ability to explain mathematical concepts and processes. The document provides clear explanations and calculations for each problem, ensuring a comprehensive understanding of the concepts involved. The solutions cover topics from basic algebra to more advanced concepts, offering a complete overview of the mathematical principles covered in the assignment.

TMA 02 Mathematics

1. (y-3)/(2y+7)>=0
Step 1: Writing the inequality in the correct form.
(y-3) / (2y+7)>=0
Step 2: Finding the critical values by setting the numerator and denominator of the
fraction equal to zero and solving.
y-3=0 and 2y+7=0
y=3 and y= -7/2
Step 3: Making of sign analysis chart by using the key values found in step 2 for dividing
the line into sections.
-7/2 3
Step 4: Performing the sign analysis by picking the number from each section which are
created in step 3 and plugging them into the polynomial for determining the sign of the
answer. When y=-8/2, result is 7, when y=0, result is -3/7 i.e., a negative value and when
y= 4, result is 1/ 15.
+ - +
-7/2 3
Step 5: Using the sign analysis chart for determining the sections which satisfied the
inequality. When y = 0, it is giving the value which is undefined and when y = -7/2 then
it is giving negative value which does not satisfy the inequality. This is why, open circle
is used instead of closed circle for drawing the graph.
-7/2 3
2

Step 6: (- ∞, -7/2) ∪ [3, ∞)
2. f (t)=Bekt (t>=0)
Density after 2 hours = 0.0436 AU
Density after 6 hours = 0.0978 AU
a. k=0.202
t=2
e=2.718
f (t)=0.0436 AU
f (t)=Bekt
0.0436=B * e0.202*2
0.0436=B * e0.404
0.0436/1.4978=B
B= 0.0291
b. k=0.202
t=9
e=2.718
f (t)=Bekt
f (t)=0.029* e0.202*9
f (t)=0.029* e1.818
f (t)=0.029* 6.1595
f (t)=0.178
3. a. f (x)= (x-3)2-2 y=x2
i.
3

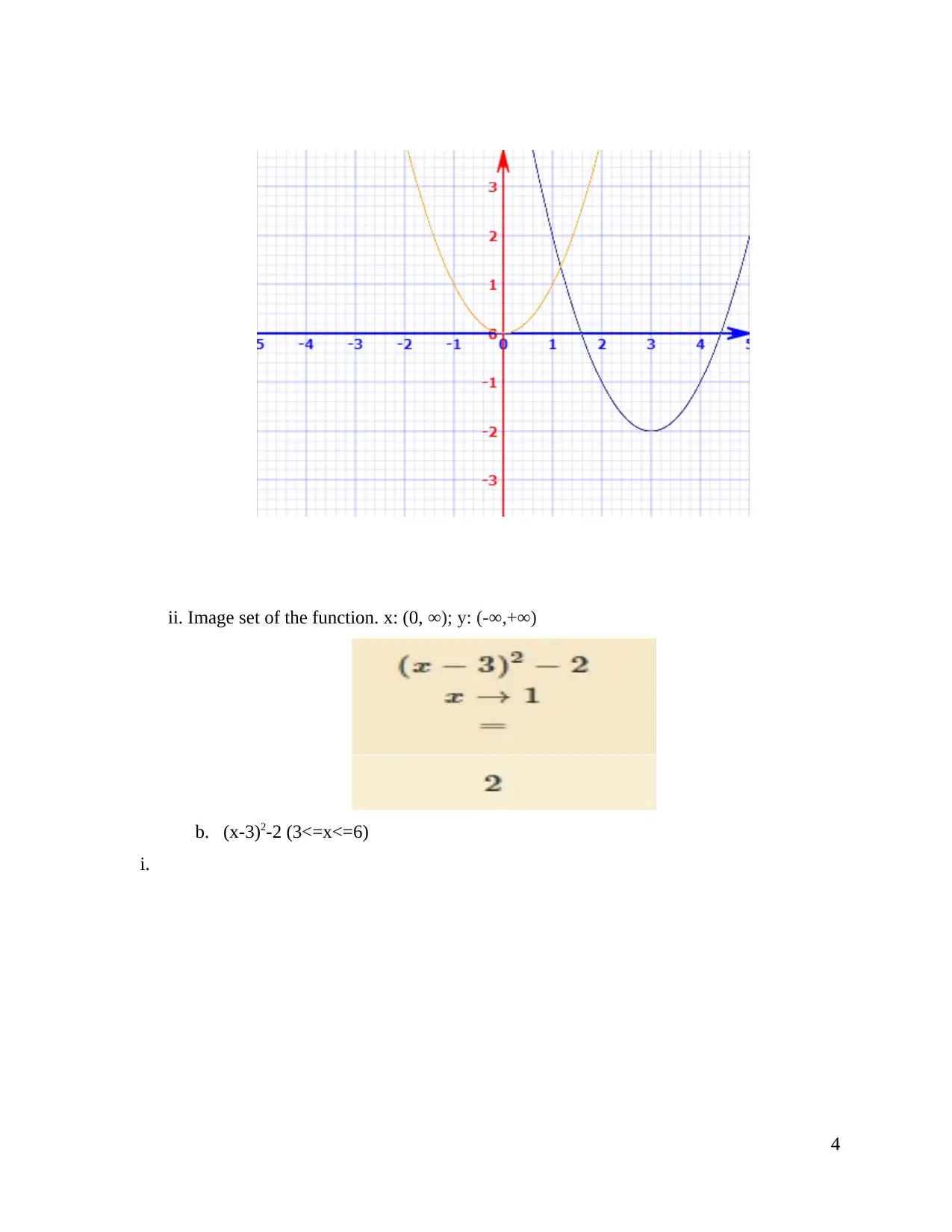
ii. Image set of the function. x: (0, ∞); y: (-∞,+∞)
b. (x-3)2-2 (3<=x<=6)
i.
4

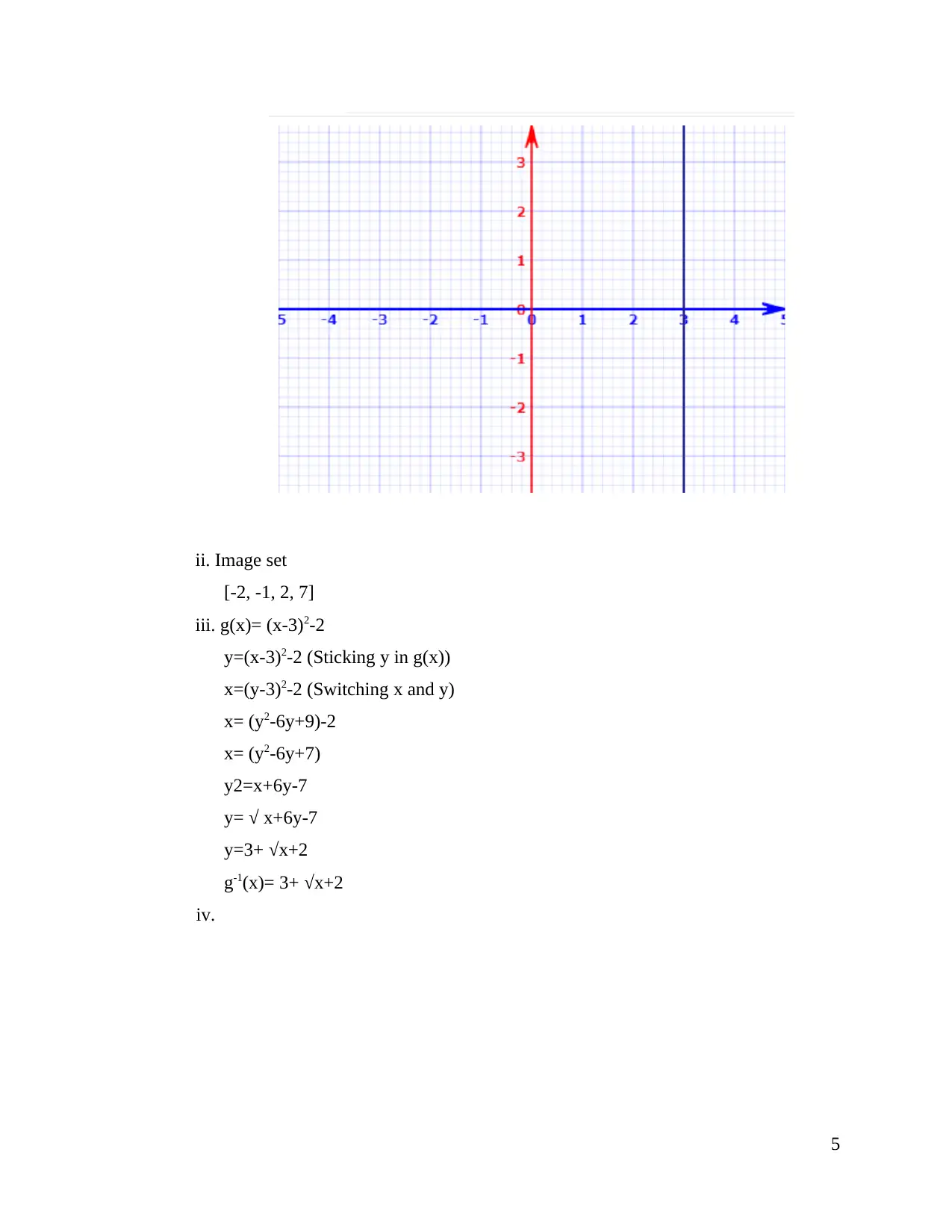
ii. Image set
[-2, -1, 2, 7]
iii. g(x)= (x-3)2-2
y=(x-3)2-2 (Sticking y in g(x))
x=(y-3)2-2 (Switching x and y)
x= (y2-6y+9)-2
x= (y2-6y+7)
y2=x+6y-7
y= √ x+6y-7
y=3+ √x+2
g-1(x)= 3+ √x+2
iv.
5

4. a. a=9 cm
b=11 cm
Angle C=32°
Area= (a*b*Sin C)/ 2
= (9*11*Sin 32°)/ 2
= (99*0.529)/2
= 52.371/2
= 26.18 cm2
b. i. Cosine rule is a2=b2+c2-2bc Cos(α)
c2=a2+b2-2ab Cos(α)
c2=92+112-2*9*11 Cos(32°)
c2=81+121-198*0.848
c2=202-167.90
c2=34.1
c=5.84 cm
i. Area of triangle= √p(p-a)(p-b)(p-c)
p= (a+b+c)/2
6

= (9+11+5.84)/2
= 25.84/2
= 12.92
Area = √12.92 (12.92-9)(12.92-11)(12.92-5.84)
= √12.92 (3.92)(1.92)(7.08)
= √688.46
Area = 26.23 cm2
Therefore, the area found is same as the area find above.
c. a/ Sine A= b/ Sine B= c/Sine C
9/Sine A=11/Sine B=5.84/Sine 32°
11/Sine B=5.84/0.529
11*0.529=Sine B*5.84
5.819/5.84=Sine B
Sine B= 0.996
Sin-1 (0.996) = 84.87
B=84.87°
9/Sine A=11/Sine 84.87°
Sine A= (9*0.996)/11
= 0.815
A= Sine-1(0.815)
A = 54.59°
5. a. Sin (A-B) = Sin A. Cos B – Cos A. Sin B
Sin (A+B) = Sin A. Cos B + Cos A. Sin B
Knowing that 5π/12= π/4+ π/6
Sin (5π/12) = Sine (π/4+ π/6)
= Sin (π/4) Cos (π/6) + Cos (π/4) Sin (π/6)
= √2/2. √3/2 + √2/2.1/2
= (√6 + √2)/4
b. By using the half angle formula,
7

Cos (θ/2) = √ {1+Cos (θ)}/2
If θ/2 = 5π/12
Then, θ=5π/6
This is already known that 5π/6 is considered as a standard angle in the 2nd quadrant with
reference angle of π/6.
So, Cos (5π/6) = -Cos (π/6) = -√3/2
Therefore,
Cos (5π/12) = √ {(1-√3/2)/2}
= √ [{(2-√3)/2}/2]
= √ {(2-√3)/4}
= √ {(2-√3)}/ 2
c. To prove: Sin2θ+Cos2θ = 1
Sin2 (5π/12) + Cos2 (5π/12) = 1
[(√6 + √2)/4]2 + [√ {(2-√3)}/ 2]2
= (√6 + √2)2/16 + [√ (2-√3)] 2 /4
= {(√6)2+2*√6*√2}/16 + [√ {(22-2*2*√3+√32)}] 2 /4
= (8+2√12)/16 + (7-4√3)/4
= 1
6. Parabola y =3x2-6x-1
Ellipse: 4x2 + 25y2-32x-100y + 64 =0
8

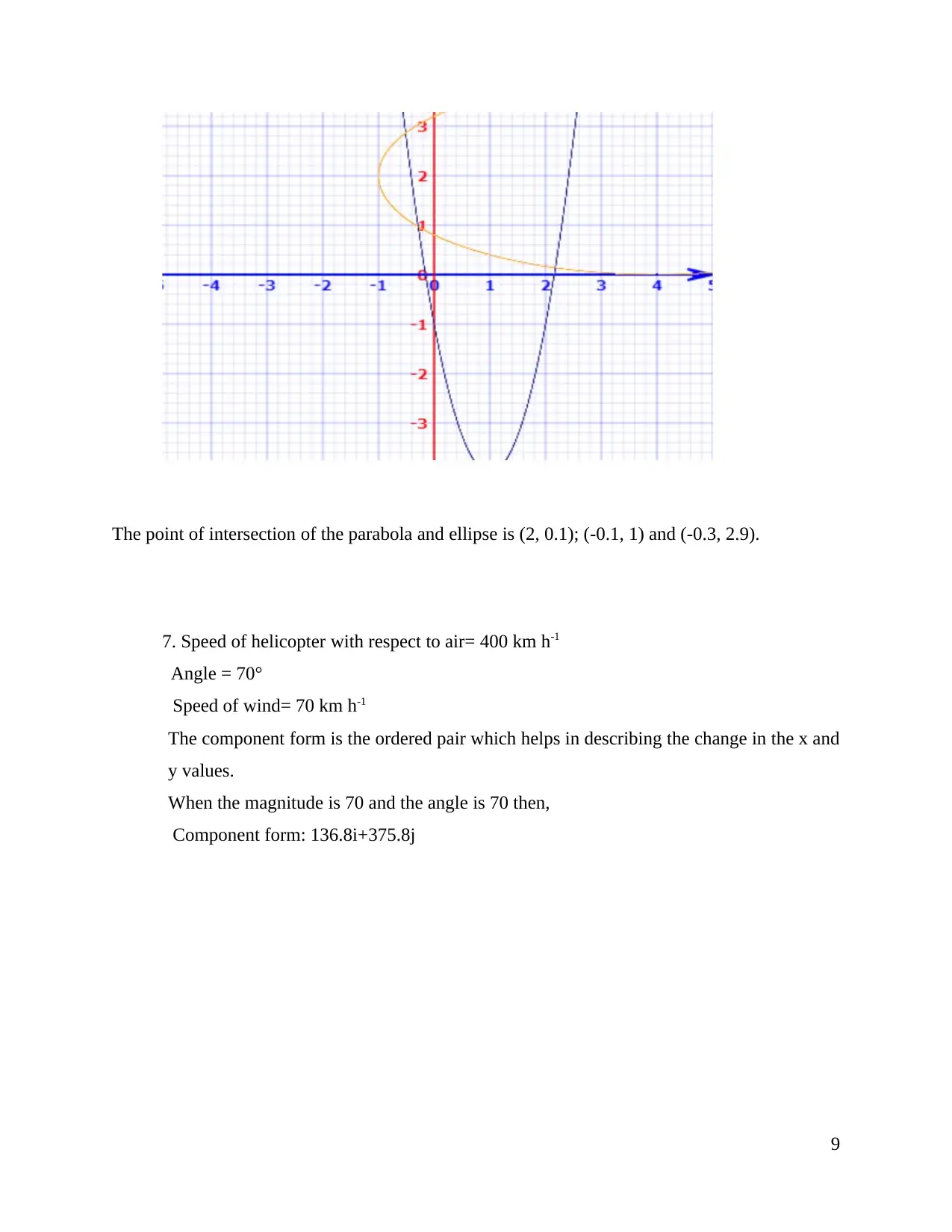
The point of intersection of the parabola and ellipse is (2, 0.1); (-0.1, 1) and (-0.3, 2.9).
7. Speed of helicopter with respect to air= 400 km h-1
Angle = 70°
Speed of wind= 70 km h-1
The component form is the ordered pair which helps in describing the change in the x and
y values.
When the magnitude is 70 and the angle is 70 then,
Component form: 136.8i+375.8j
9

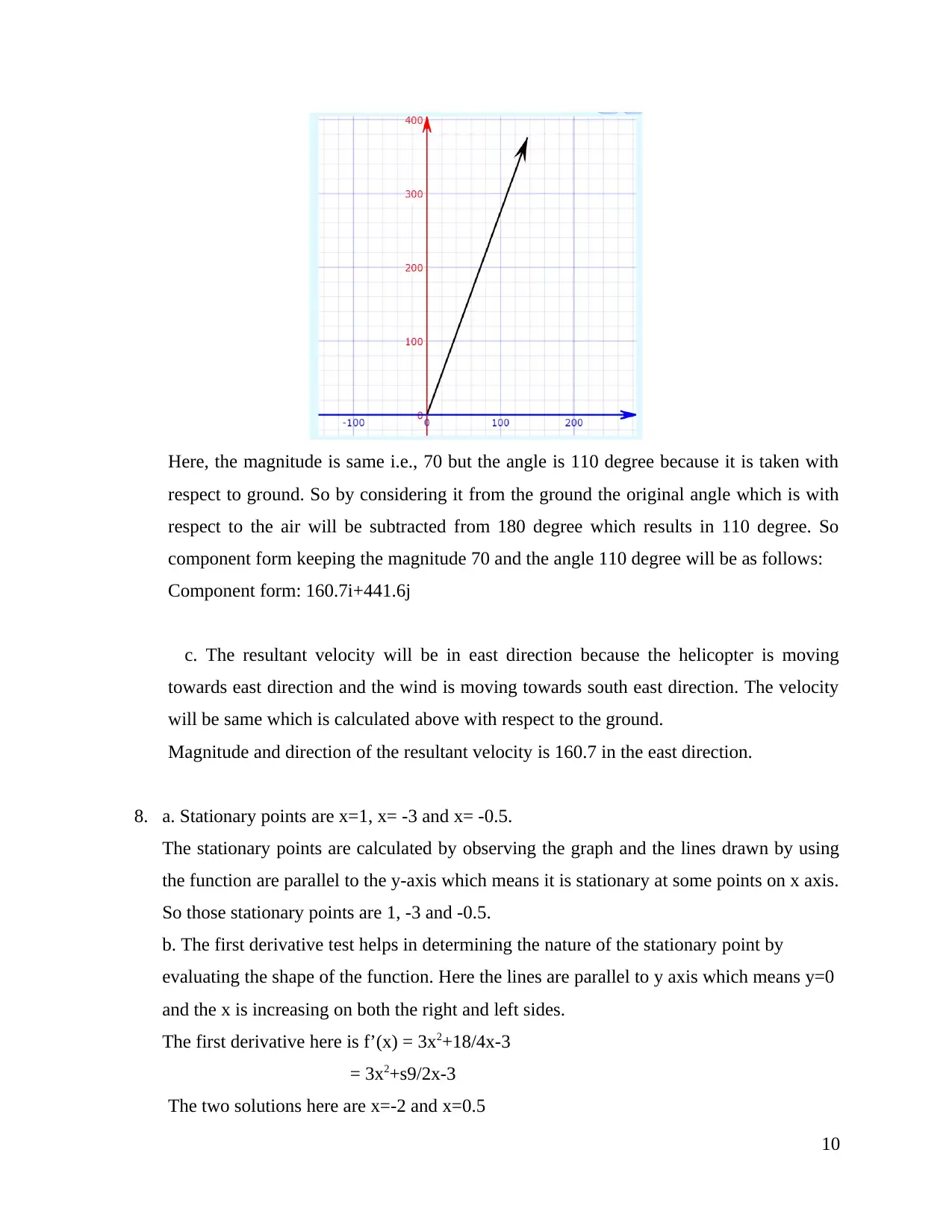
Here, the magnitude is same i.e., 70 but the angle is 110 degree because it is taken with
respect to ground. So by considering it from the ground the original angle which is with
respect to the air will be subtracted from 180 degree which results in 110 degree. So
component form keeping the magnitude 70 and the angle 110 degree will be as follows:
Component form: 160.7i+441.6j
c. The resultant velocity will be in east direction because the helicopter is moving
towards east direction and the wind is moving towards south east direction. The velocity
will be same which is calculated above with respect to the ground.
Magnitude and direction of the resultant velocity is 160.7 in the east direction.
8. a. Stationary points are x=1, x= -3 and x= -0.5.
The stationary points are calculated by observing the graph and the lines drawn by using
the function are parallel to the y-axis which means it is stationary at some points on x axis.
So those stationary points are 1, -3 and -0.5.
b. The first derivative test helps in determining the nature of the stationary point by
evaluating the shape of the function. Here the lines are parallel to y axis which means y=0
and the x is increasing on both the right and left sides.
The first derivative here is f’(x) = 3x2+18/4x-3
= 3x2+s9/2x-3
The two solutions here are x=-2 and x=0.5
10

c.
d. The least value is ¼ and the greatest value of the function is 9.
This is calculated by putting -3and 2 in the function
f (x)= x3+9/42-3x-2
When x=-3, then f(x) = ¼ and when x=2, then f(x) = 9.
9. a. Expression: x(t) = x0+v0t+at2/2
b. Expression: y = m x + c
a = m t + c
c. The velocity is the lowest when the acceleration changes the direction. The
minimum speed will be given by v(t).
This will happen when the t=0 in the given equation.
10. Mathematical communication is basically development of the collecting resources in
order to involve the students for speaking and writing about the mathematics. This is
mainly done to learn maths or to communicate as maths.
The maths of the equations and the graphs was mainly highlighted. This also helped in
gaining deeper insight about the trigonometric ratios such as sine and cosines at
11

different angles. The graphs of the inequalities were also communicated through this.
Various concepts regarding the speed, time, acceleration etc. were highlighted.
Furthermore, the vector form was also converted into component form helping in
gaining insight about the directions.
12