Maths for Computing Assignment: Calculus, Vectors and Geometry

This assignment solution for Maths for Computing covers several key areas of mathematics relevant to computing. It begins with number theory, including converting decimal numbers to binary, octal, and hexadecimal formats, and applying modular arithmetic to solve practical problems. The assignment also includes Python code for calculating GCD and LCM. The section on sequence and series addresses cost estimation and depreciation calculations. Probability theory is explored through component failure analysis and battery selection scenarios. Probability distributions are examined using coin toss experiments. The assignment further delves into geometry, covering coordinate conversions and ladder/pylon problems, as well as surveyor calculations. Vector analysis is applied to ship navigation and force resolution problems. Finally, differential and integral calculus concepts are touched upon, demonstrating their application in solving related problems. Desklib provides a platform for students to access past papers and solved assignments like this one to aid in their studies.

Maths for Computing

Contents
LO1: Use applied number theory in practical computing scenarios..........................................2
Part 1 Number Theory............................................................................................................2
LO2: Analyses events using probability theory and probability distributions.........................10
Part 1 probability..................................................................................................................10
Part 2: Probability Distribution............................................................................................12
LO3: Determine solutions of graphical examples using geometry and vector methods..........13
Part 1: Geometr....................................................................................................................13
Part 2: Vectors......................................................................................................................16
LO4: Evaluate problems concerning differential and integral calculus...................................17
Part 1 Differential Calculus..................................................................................................17
Part 2 integral calculus.........................................................................................................19
References................................................................................................................................20
1

LO1: Use applied number theory in practical computing scenarios.
Part 1 Number Theory
[P1]
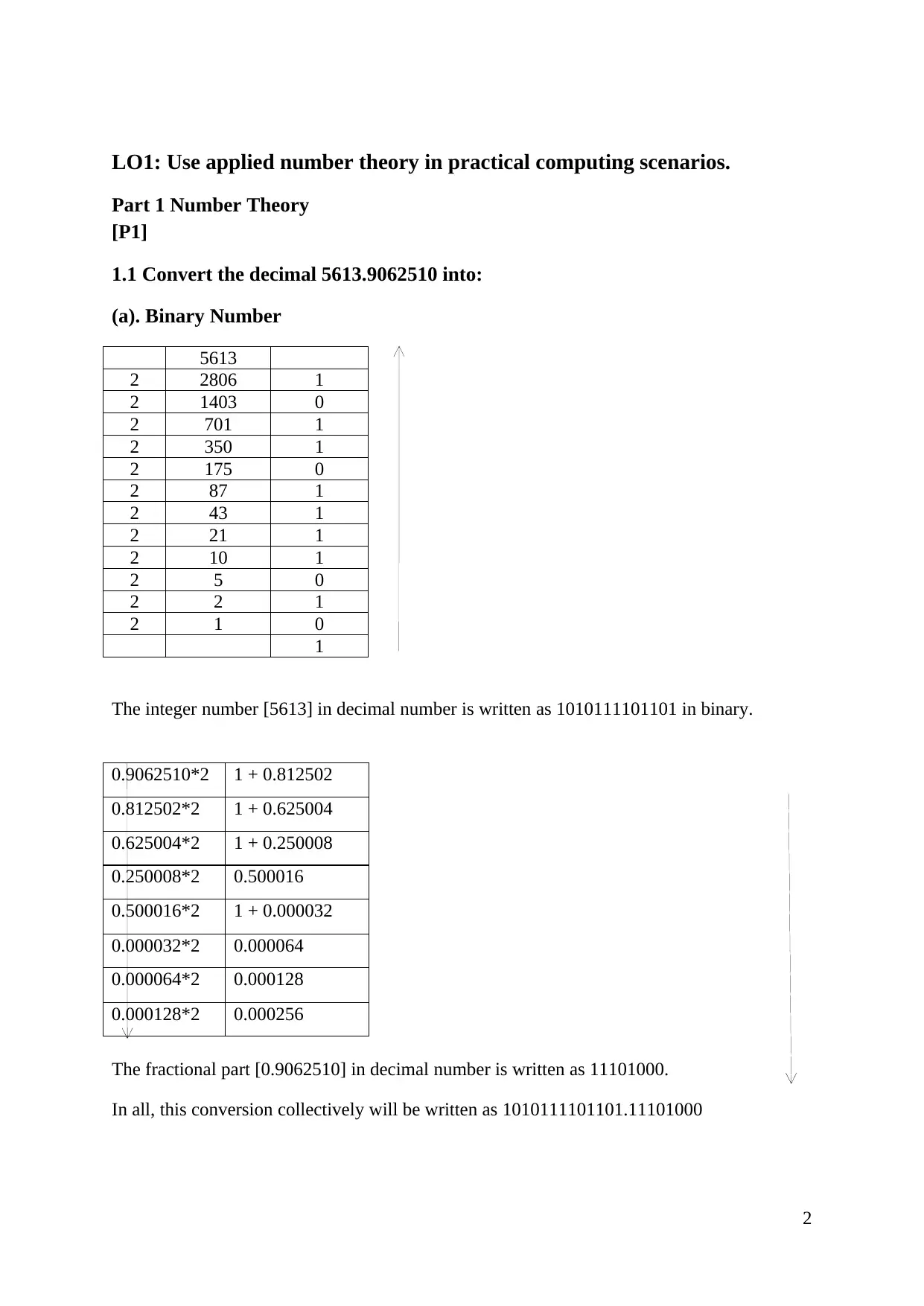
1.1 Convert the decimal 5613.9062510 into:
(a). Binary Number
5613
2 2806 1
2 1403 0
2 701 1
2 350 1
2 175 0
2 87 1
2 43 1
2 21 1
2 10 1
2 5 0
2 2 1
2 1 0
1
The integer number [5613] in decimal number is written as 1010111101101 in binary.
The fractional part [0.9062510] in decimal number is written as 11101000.
In all, this conversion collectively will be written as 1010111101101.11101000
2
0.9062510*2 1 + 0.812502
0.812502*2 1 + 0.625004
0.625004*2 1 + 0.250008
0.250008*2 0.500016
0.500016*2 1 + 0.000032
0.000032*2 0.000064
0.000064*2 0.000128
0.000128*2 0.000256

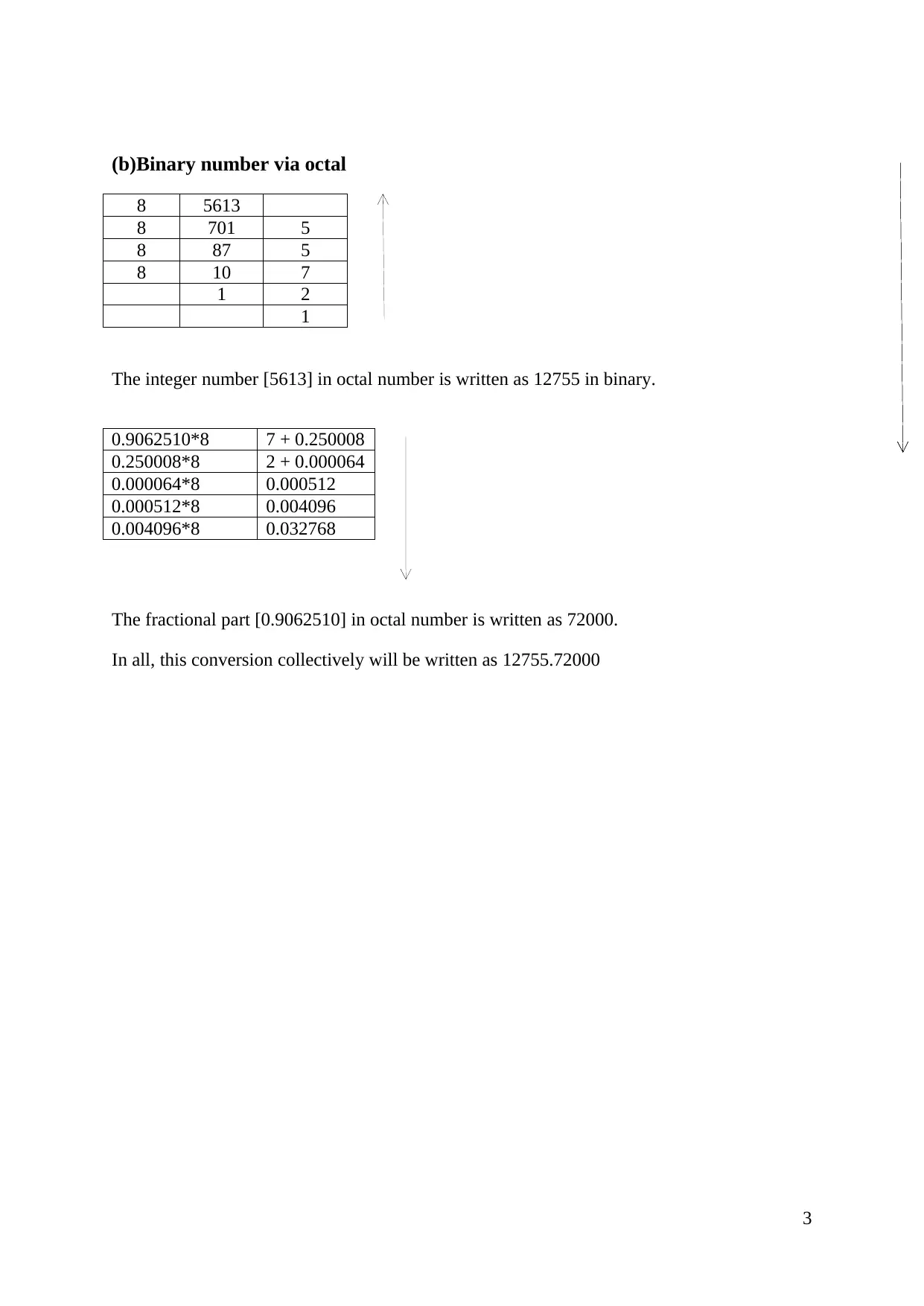
(b)Binary number via octal
8 5613
8 701 5
8 87 5
8 10 7
1 2
1
The integer number [5613] in octal number is written as 12755 in binary.
The fractional part [0.9062510] in octal number is written as 72000.
In all, this conversion collectively will be written as 12755.72000
3
0.9062510*8 7 + 0.250008
0.250008*8 2 + 0.000064
0.000064*8 0.000512
0.000512*8 0.004096
0.004096*8 0.032768

(c) Hexadecimal
5613.9062510
5613- Consider bottom-up
16 5613
16 350 13(D)
16 21 14(E)
1 5
1
.9062510 consider Top-down
16*.0962510= 14.500016
16*500016=8.000256
16*000256=0.004096
16*004096=0.065536
16*0.065536=1. 048576
The resultant conversion is=15ED.E8001 (Decimal to Hexadecimal)
4

M1- A shop owner receives 40 boxes of bottled water in one delivery. Each box
contains 110 bottles of water. The shop owner plans to pack the bottles into cases
of 12 to sell. After making as many complete cases as possible, how many bottles
will be leftover? Use modular arithmetic to give answer.
Total boxes of bottled water in one delivery = 40
1 box has= 110 bottles
So Total bottles = 40 × 110 =4400
One Pack has ha total bottle = 12
Modular Arithmetic
A= (Total bottles) % (total bottles in 1 pack)
% represents the mod sign i.e. A represent the mod of total bottles and total bottles in 1 pack
Suppose B = bottles left
B = A× (total bottles in 1 pack)/100
A= 4400%12
= 67
B = 67 × 12 /100
=> 8
8 bottles will be leftover.
Python code to calculate GCD:
number1 = 60
number2 = 40
if number1 > number2:
small = number2
else:
small = first
for num in range(1, small+1):
if ((number1 % num == 0) and (number2 % num == 0)):
HCFoutput = num
5

print("First Number:"+ str(number1))
print("Second Number:"+str(number2))
print("GCD:", str(HCFoutput))
Python code for LCM:
number1 = 60
number2 = 40
LCMResult=0
if number1> number2:
greater= number1
else:
greater = number2
while(True):
if(( greater% number1 == 0) and (greater % number2== 0)):
LCMResult = greater
break
greater += 1
print("First Number:"+ str(number1))
print("Second Number is:"+str(number2))
print("The LCM is:", str(LCMResult))
6

Part 2: Sequence and series
1.3-An oil company bores a hole 100m deep. Estimating the cost of boring if the
cost is £50 for drilling the first meter with an increase in cost of£5 per meter for
each succeeding meter
First meter cost = £50
Second meter cost = £55
Third meter cost = £60
There is a create a Sequence
50 +55+60+65+70……..until 100 meter
Sn = n
2 [a+an]
Here a = 55 n= 100
An = a+ (n-1) d
Here, d = 5
= 50+ (100-1)×5
= 545
Sn = 100
2 [50+545]
= 29750
1.4-An industrial machine originally valued at 30000 when brand new
depreciates at a rate of 12 per annum. Based on this data, answer the following
question.
a) calculate its value after years
b) The company policy is to sell the machine when its value drops below 5000.
After how many years will the machines be sold
A) Present value of machine = £30000
Rate of depreciation =12%
7

[Final Value = Actual value – Depreciated value]
After the 1 st year machine value = 30000- (.12* 30000)
= 26400
After the 2nd year machine value = 26400- (.12* 26400)
= 23232
After the 3rd year machine value = 23232- (.12* 23232)
=20444.16
After the 4th year machine value = 20444.16- (.12* 20444.16)
= 17990.87
After the 5th year machine value = 17990.87- (.12* 17990.87)
= 15831.96
Price of 5 year later machine = £831.96
B) After the 15 years machine price is below 5000.
8

LO2: Analyses events using probability theory and probability
distributions
Part 1 probability
2.1- The probability of a component failing in one year due to excessive
temperature is 0.05, due to excessive vibrations is 0.04 and due to excessive
humidity is 0.02. Determine the probability that during a one year period a
component:
(a) Fails due to excessive temperature and excessive vibration
(b) Fails due to excessive vibration or excessive humidity
(c) Will not fail because of both excessive temperature and excessive humidity.
The probabilities of the failing component within one year are:
P (Temp) = 0.05, P (Vibration) = 0.04, P (Humidity) = 0.02
a) Fail due to excessive temperature and excessive vibration
Let the probability P (failed) be failed due to excessive temperature and vibration
P (failed) = P (Temp) × P (Vibration) = 0.002
b) Failure due to the extreme humidity or the vibration
Let probability P (failure) be because of failed extreme humidity or the vibration
P (failure) = P (Vibration) + P (Humidity) = 0.06
c) Not failed because of both extreme humidity and the extreme temperature.
Let probability P (notfail) be because of both extreme humidity and the extreme
temperature
P’ (noHumidity) = 1- P (Humidity) = 0.98
P (noTemp) = 1- P (Temp) = 0.95
P (notfail) = P (noTemp) × P (noHumidity) = 0.931
2.2- A batch of 50 mobile phone batteries contains 31 that are within the required
tolerance value, 8, which are below the required tolerance values. Determine the
probability that when randomly selecting a battery and then a second battery
(a) Both are within the required tolerance values when selecting with
replacement, and
(b) The first one drawn is below and the second one drawn is above the required
tolerance value, when selection is without replacement.
Total batteries are: 50
Batteries within tolerance value: 31
9

Batteries below tolerance value: 08
Batteries above tolerance value: 11
a) The batteries within tolerance value is: 31
P (with) = 31
50 =0.62
So, probability of both batteries are:
0.622 = 0.39
b) The one battery is below the tolerance value,
Other is above the tolerance value.
P (below) = 8
50 =0.16, now one is occupied so number of batteries left is:
P (above) = 11
49 =0.2245
So, probability of both batteries are: 0.2245.
10

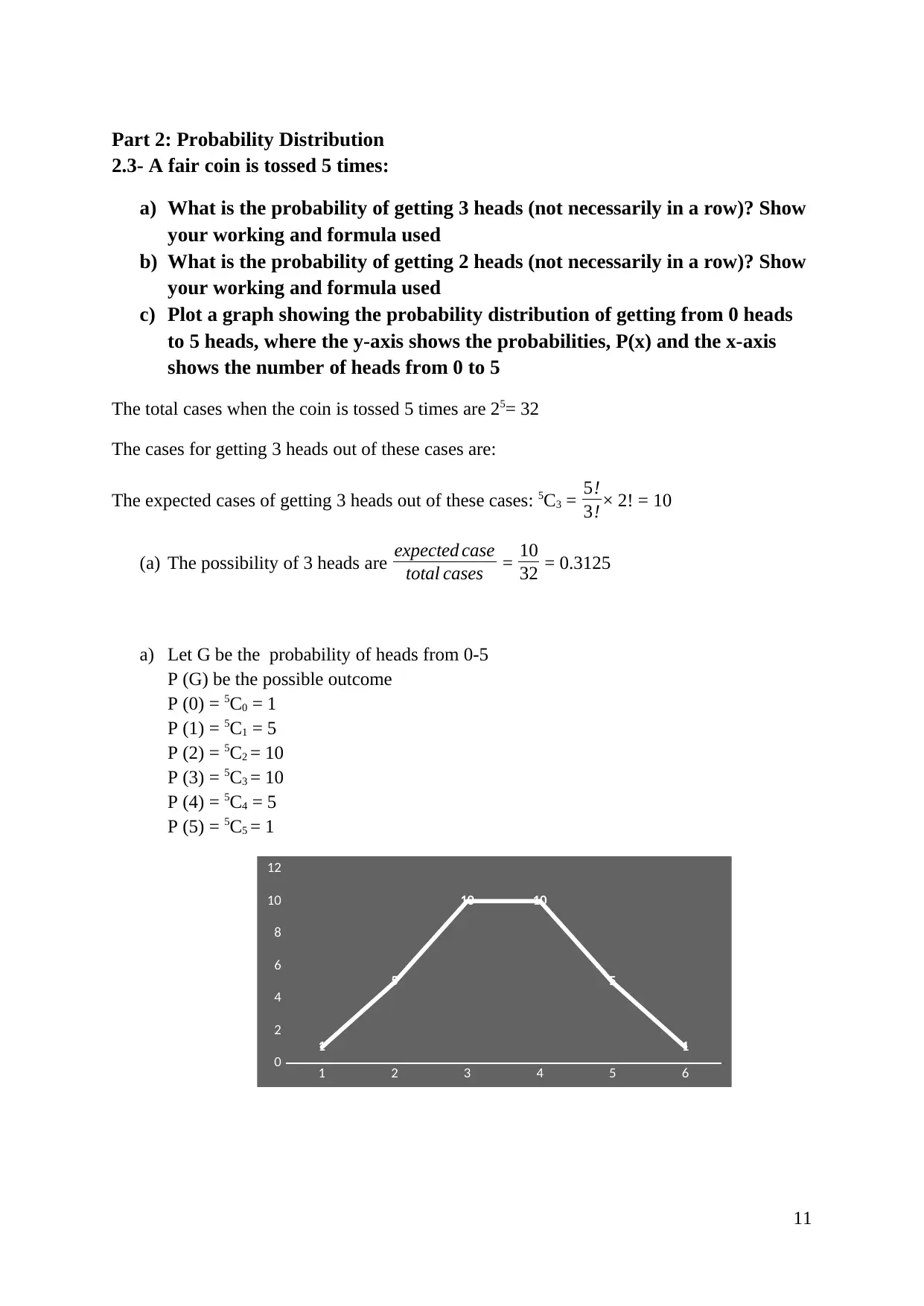
Part 2: Probability Distribution
2.3- A fair coin is tossed 5 times:
a) What is the probability of getting 3 heads (not necessarily in a row)? Show
your working and formula used
b) What is the probability of getting 2 heads (not necessarily in a row)? Show
your working and formula used
c) Plot a graph showing the probability distribution of getting from 0 heads
to 5 heads, where the y-axis shows the probabilities, P(x) and the x-axis
shows the number of heads from 0 to 5
The total cases when the coin is tossed 5 times are 25= 32
The cases for getting 3 heads out of these cases are:
The expected cases of getting 3 heads out of these cases: 5C3 = 5!
3! × 2! = 10
(a) The possibility of 3 heads are expected case
total cases = 10
32 = 0.3125
a) Let G be the probability of heads from 0-5
P (G) be the possible outcome
P (0) = 5C0 = 1
P (1) = 5C1 = 5
P (2) = 5C2 = 10
P (3) = 5C3 = 10
P (4) = 5C4 = 5
P (5) = 5C5 = 1
11
1 2 3 4 5 6
0
2
4
6
8
10
12
1
5
10 10
5
1

LO3: Determine solutions of graphical examples using geometry and vector
methods
Part 1: Geometr
3.1- change the following Cartesian co-ordinates in into polar co-ordinate, and
the polar co-ordinate into Cartesian co-ordinate -in both cases your answer must
be correct to 2 decimal places
 (-2.3, 5.4)
x = r*cos(θ) - (1) y = r*sin(θ) - (2)
Squaring and adding 1,2 equations
r2 = x2+y2
r2 =(-2.3)2+ (5.4)2
r = 5.87
As it’s the length so only positive allowed.
tan(θ) = 5.4
−2.3 = -2.34 = 113.50
Hence, the polar coordinates are (5.87, 113.5○) (Tutorial.math.lamar.edu, 2018)
 (7.6, −9.2)
x = r*cos(θ) - (1) y = r*sin(θ) - (2)
Squaring and adding 1,2 equations
r2 = x2+y2
r2 = 7.62 + (-9.2)2
r = 11.93
As it’s the length so only positive allowed.
tan θ = 7.6
−9.2 = -0.826
θ = 320.50
Hence, the polar coordinates are (11.93, 320.5○) (Tutorial.math.lamar.edu, 2018)
 (6.5, 1320)
x = r*cos(θ) - (1) y = r*sin(θ) - (2)
Squaring and adding 1,2 equations
r2 = x2+y2
r2= 6.52+13202 => r= 1320.02 because its length.
tan (θ) = 1320/6.5
θ = 89.720
Hence, the polar coordinate are (1320.02, 89.72○) (Tutorial.math.lamar.edu, 2018)
 (3, 3rad)
3rad= 171.90
x = r*cos( θ )
x = 3*cos (171.9○) => -2.97
y = r*sin(θ )
12

y = 3*sin (1719○) => 0.42
Hence, the polar coordinate are (-2.97, 0.42). (Tutorial.math.lamar.edu, 2018)
3.2- A 2m long ladder is placed against a perpendicular pylon with its foot 52cm
from the pylon. Find how far up the pylon (correct to nearest mm) the ladder
reaches if the foot of ladder is moved 10cm toward the pylon how far does the top
of ladder rise?
Height of pylon up to top of ladder:
 (p)2+ (f)2 =(l)2
 (p)2 + 522 =2002
 p=193.12 cm.
 2002 = 422 + (193.12+p)2
 40000 = 1764 + (193.12+p)2
 193.12+p =±195.54
13

 Only positive as its length
 hence, p = 2.42 cm = 24.2 mm (Khan Academy, 2018)
3.3- From a point on horizontal ground a surveyor measures the angle of
elevation of a church spine is 15○. He moves 30 m nearer to the church and
measure the angle of elevation as 20○ calculate the height of the spire.
 tan ( 200 ) => B/H = H * 0.364 (1)
 tan ( 150 ) => B = (H+30) * 0.268 (2)
 Comparing equation 1 and 2
 0.364H = 0.268H + 8.04
 0.096H = 8.04
 H = 83.75m
 using equation 1
 B = 83.75 ×0.364 = 30.40
 Hence, height is 30.40 m (Khan Academy, 2018)
14

Part 2: Vectors
3.4- a ship heads on a course due to south at 12kmph. It is moved off course by a
current flowing in a north-eastern direction at 8kmph. Determine the resultant
velocity
 Ship direction to south at 12km/h
 Wind current direction to north east at 8km/hr.
 Hence velocity is
 V = √144−64
 V = 8.944km/hr (Math.oregonstate.edu, 2018)
3.5- Two forces F1 and F2 with magnitude 20N and 30n, respectively, act on an
object at a point P as shown in the figure below. Find the resultant forces acting
at P.
 Force with horizontal axis
 F1cos450 − F2cos300 = −11.84
 Force with vertical axis
 F2sin600+ F1sin450 = 40.12
 R= √ ( −11.84 ) ( −11.84 ) +(40.12)( 40.12) => 41.85 N
 tanθ = 40.12
−11.84
 θ = 16.44 from y axis (Math.oregonstate.edu, 2018)
15

LO4: Evaluate problems concerning differential and integral calculus
Part 1 Differential Calculus
4.1- You have been asked to analyse a motherboard to access the lifespan of the
capacitors. When a charged capacitor is connected to a resister to form an RC
(resistor-capacitor) circuit, the capacitor discharge follows the equation:
V (t) = Vmaxe-t/5
Where v is the voltage, t is the time in seconds, and Vmax is the initial voltage
a) Determine the rate of the discharge at t= 10ms.
b) Calculate the time when the discharge rate half of what is at 10ms
 Its given that capacitor’s rates analysed by given equation:
V (t) = Vmaxe-t/5
 Discharge rate of capacitor:
V’ (t) = −(Vmaxe-t/5)/5
 t = 10 seconds
V’ (10) = −(Vmaxe-10/5)/5 =>−Vmax÷ (5 × e2) =>−Vmax÷ 36.94 =>−0.027 × Vmax
 New rate of discharge half of V’(10)
 So, new value of discharge = −0.0135 × Vmax
 According to above equation of discharge :−(Vmaxe-t/5)/5
 After there:, −0.0135 × Vmax= −(Vmaxe-t/5)/5
 0.0135 × 5 = e-t/5
 0.0675 = e-t/5
 et/5 = 14.81
 t/5= 2.69
 t = 13.48 seconds
16

4.2- The fuel economy E of a car, in miles per gallon, is given by:
E = 21+2.1×10-2V2−3.80×10-6V4
Where v is the speed of car in miles per hour. Determine, correct to 3 significant
figures, the most economical fuel consumption, and the speed at which it is
achieved.
 E = 21+2.1×10-2V2−3.80×10-6V4
 d(E) = 0
 4.2×10-3×V – 15.2×10-6×V3 = 0
 V2= 276.31
 V=16.62 mi/hr
 E= 21+2.1×10-2×276.31−3.80×10-6×76347.21
 E=26.51
17

Part 2 integral calculus
4.3- the sales (s) of a computer game in the first t years of its release can be
approximated by the function:
S (t) = t√0.5(t∗t )+ 2
where the sales (s) is measured in millions of pound.
using integration, estimate the average yearly sales over the first five years of the
game's release
 s(t) = t√0.5(t∗t )+ 2 => s(t) = √0.5 (t√ (t∗t)+ 4 )
 ∫ s (t) = ∫ √0.5(t √(t∗t )+ 4) = ¿ )(t2 + 4)3/2
 ∫
0
5
s (t)=> 34.89.
4.4- the vertical height h (in km) of missile varies with the horizontal distance d
(in km), and is given by h=4d-d2. Determine the mean height of missile from d=0
to d= 4km.
Let z be the mean
 h => 4d – d2
now integrate h to calculate the average value
 ∫
0
4
4 d – d∗d = (4y – y2)(4-0)
Now putting the value of the in the definite integral
 [ 4 (d∗d)
2 −( d∗d∗d)
3 ¿40 = (4y – y2)4
 4y – y2 = 8/3
 y = 3.17
18

References
 Khan Academy (2018). High School Geometry |Khan Academy. [online]. Available
at: https://www.khanacademy.org/math/geometry [Accessed 18 Apr. 2018].
 Math.oregonstate.edu (2018). Study Guide for Vector Calculus. [online]. Available at:
https://math.oregonstate.edu/home/programs/undergrad/CalculusQuestStudyGuides/
vcalc/vcalc.html [Accessed 18 Apr. 2018].
 Tutorial.math.lamar.edu (2018). Calculus II - Polar Coordinates. [online]. Available
at: http://tutorial.math.lamar.edu/Classes/CalcII/PolarCoordinates.aspx [Accessed 18
Apr. 2018].
19