Maths Modelling and Decision Analysis Assignment: Investment Portfolio
VerifiedAdded on 2022/09/18
|8
|1272
|26
Homework Assignment
AI Summary
This assignment focuses on applying linear programming to solve a real-world investment problem faced by SoapMax Limited. The report begins with an introduction to linear programming and its applications in business decision-making, followed by a detailed description of the investment problem. SoapMax is presented with five investment options, each with different cash inflows and outflows over a four-year period, and the challenge is to select the optimal portfolio given limited capital. The assignment then outlines the linear programming formulation, including decision variables (investment choices), the objective function (maximizing net present value), and constraints (capital limitations). The problem is solved using Excel Solver, and the results are analyzed to determine the optimal investment mix. The report concludes by discussing the implications of the solution, highlighting the projects to invest in to maximize NPV and the binding constraints. The assignment demonstrates how linear programming can enhance decision-making processes and improve profitability.

Maths Modelling and Decision Analysis
Student Name
Institution Name
1
Student Name
Institution Name
1
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Introduction
In the real business world, there are always a set of decisions that need to be made by the
management of firms. The decisions often entail consideration of several variables that would be
tiresome to take into account. The use of linear programming is thereby mean to offer assistance
in such circumstances. The concept of linear programming is applied in operations research to
obtain optimal solutions. Application of linear programming allows the decision, maker to settle
for the best and most economical solution for a specific problem (Chanda, 2013). This carters for
all the involved limitations and give a clue of how well the limited resources can be put to use so
as to optimize the outcome of the decision. Liner programming is applied in several fields to
ensure the processes are more efficient. Areas such as engineering, transportation, agriculture,
energy as well as manufacturing can be enhanced by application of linear programming concept.
While it may be possible to Undertale manual liner programming, business scenarios are
occasionally very complex and thereby need the use of computational software (Edem, et al.,
2014). In this report the focus will be to examine and analyse how linear programming can be
applied in solving a real-world problem.
Description of the problem
To illustrate application of linear programming is solving real world problems, the report
will be based on a case study of a business phenomenon. In this case the problem to be solved is
the selection of appropriate investment opportunity. An organization (SoapMax limited) is faced
with five investments options to choose from. After undertaking a viability study of the
investments, the firm’s finance department has estimated the cashflow from the projects to be as
illustrated in the tables below.
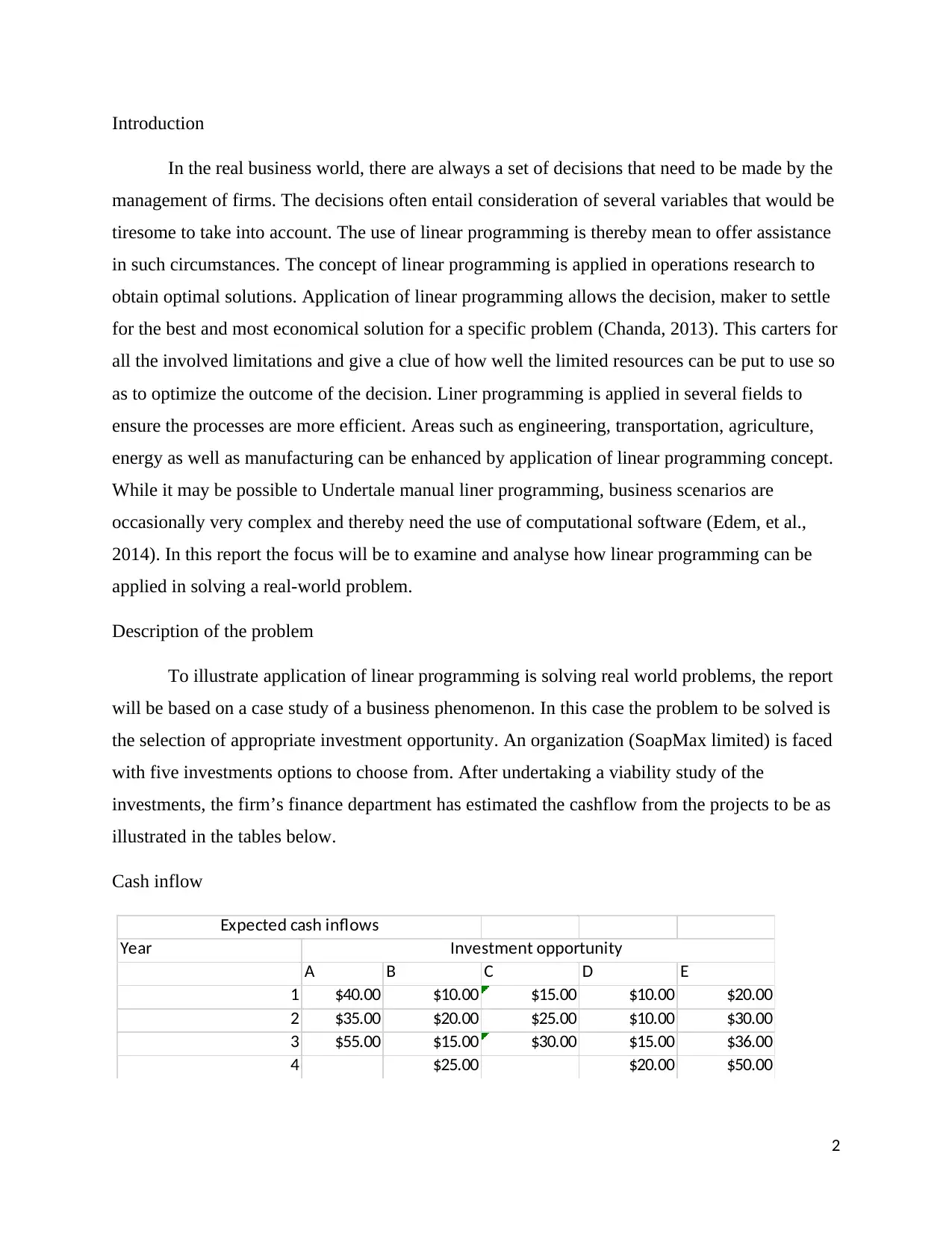
Cash inflow
Year
A B C D E
1 $40.00 $10.00 $15.00 $10.00 $20.00
2 $35.00 $20.00 $25.00 $10.00 $30.00
3 $55.00 $15.00 $30.00 $15.00 $36.00
4 $25.00 $20.00 $50.00
Investment opportunity
Expected cash inflows
2
In the real business world, there are always a set of decisions that need to be made by the
management of firms. The decisions often entail consideration of several variables that would be
tiresome to take into account. The use of linear programming is thereby mean to offer assistance
in such circumstances. The concept of linear programming is applied in operations research to
obtain optimal solutions. Application of linear programming allows the decision, maker to settle
for the best and most economical solution for a specific problem (Chanda, 2013). This carters for
all the involved limitations and give a clue of how well the limited resources can be put to use so
as to optimize the outcome of the decision. Liner programming is applied in several fields to
ensure the processes are more efficient. Areas such as engineering, transportation, agriculture,
energy as well as manufacturing can be enhanced by application of linear programming concept.
While it may be possible to Undertale manual liner programming, business scenarios are
occasionally very complex and thereby need the use of computational software (Edem, et al.,
2014). In this report the focus will be to examine and analyse how linear programming can be
applied in solving a real-world problem.
Description of the problem
To illustrate application of linear programming is solving real world problems, the report
will be based on a case study of a business phenomenon. In this case the problem to be solved is
the selection of appropriate investment opportunity. An organization (SoapMax limited) is faced
with five investments options to choose from. After undertaking a viability study of the
investments, the firm’s finance department has estimated the cashflow from the projects to be as
illustrated in the tables below.
Cash inflow
Year
A B C D E
1 $40.00 $10.00 $15.00 $10.00 $20.00
2 $35.00 $20.00 $25.00 $10.00 $30.00
3 $55.00 $15.00 $30.00 $15.00 $36.00
4 $25.00 $20.00 $50.00
Investment opportunity
Expected cash inflows
2
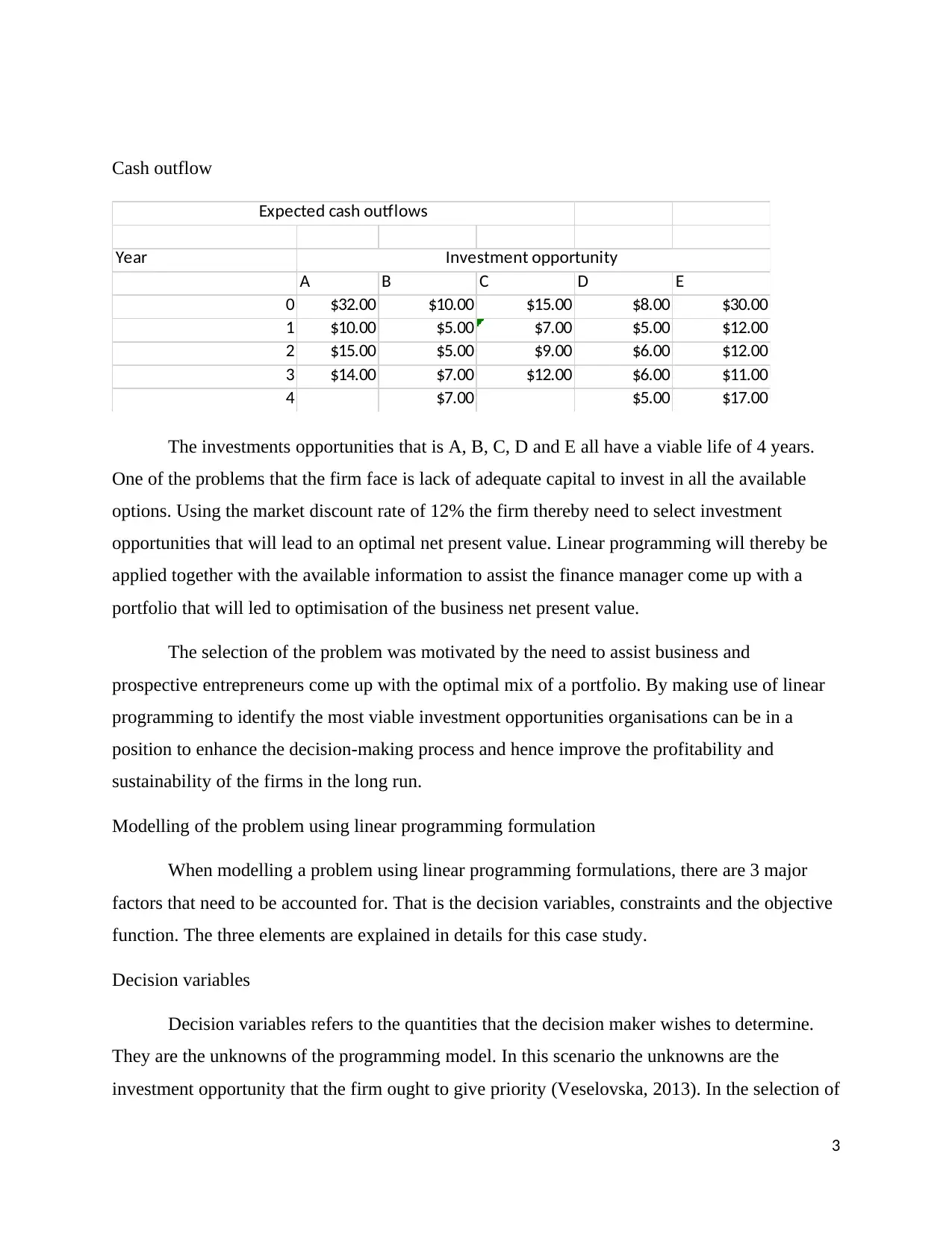
Cash outflow
Year
A B C D E
0 $32.00 $10.00 $15.00 $8.00 $30.00
1 $10.00 $5.00 $7.00 $5.00 $12.00
2 $15.00 $5.00 $9.00 $6.00 $12.00
3 $14.00 $7.00 $12.00 $6.00 $11.00
4 $7.00 $5.00 $17.00
Investment opportunity
Expected cash outflows
The investments opportunities that is A, B, C, D and E all have a viable life of 4 years.
One of the problems that the firm face is lack of adequate capital to invest in all the available
options. Using the market discount rate of 12% the firm thereby need to select investment
opportunities that will lead to an optimal net present value. Linear programming will thereby be
applied together with the available information to assist the finance manager come up with a
portfolio that will led to optimisation of the business net present value.
The selection of the problem was motivated by the need to assist business and
prospective entrepreneurs come up with the optimal mix of a portfolio. By making use of linear
programming to identify the most viable investment opportunities organisations can be in a
position to enhance the decision-making process and hence improve the profitability and
sustainability of the firms in the long run.
Modelling of the problem using linear programming formulation
When modelling a problem using linear programming formulations, there are 3 major
factors that need to be accounted for. That is the decision variables, constraints and the objective
function. The three elements are explained in details for this case study.
Decision variables
Decision variables refers to the quantities that the decision maker wishes to determine.
They are the unknowns of the programming model. In this scenario the unknowns are the
investment opportunity that the firm ought to give priority (Veselovska, 2013). In the selection of
3
Year
A B C D E
0 $32.00 $10.00 $15.00 $8.00 $30.00
1 $10.00 $5.00 $7.00 $5.00 $12.00
2 $15.00 $5.00 $9.00 $6.00 $12.00
3 $14.00 $7.00 $12.00 $6.00 $11.00
4 $7.00 $5.00 $17.00
Investment opportunity
Expected cash outflows
The investments opportunities that is A, B, C, D and E all have a viable life of 4 years.
One of the problems that the firm face is lack of adequate capital to invest in all the available
options. Using the market discount rate of 12% the firm thereby need to select investment
opportunities that will lead to an optimal net present value. Linear programming will thereby be
applied together with the available information to assist the finance manager come up with a
portfolio that will led to optimisation of the business net present value.
The selection of the problem was motivated by the need to assist business and
prospective entrepreneurs come up with the optimal mix of a portfolio. By making use of linear
programming to identify the most viable investment opportunities organisations can be in a
position to enhance the decision-making process and hence improve the profitability and
sustainability of the firms in the long run.
Modelling of the problem using linear programming formulation
When modelling a problem using linear programming formulations, there are 3 major
factors that need to be accounted for. That is the decision variables, constraints and the objective
function. The three elements are explained in details for this case study.
Decision variables
Decision variables refers to the quantities that the decision maker wishes to determine.
They are the unknowns of the programming model. In this scenario the unknowns are the
investment opportunity that the firm ought to give priority (Veselovska, 2013). In the selection of
3
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

the opportunities the value 1 will be assigned for opportunities prioritised and the value 0 for
those that have been left out. The table below indicates the decision variables.
A B C D E
Selected 1 1 1 1 1
Opportunity
Objective function
This is the quantitative criteria that is of immediate importance to the firm. In this case
study the objective is to maximise the net present value of the firm for the four-year investment
period as indicated in the table below (Gass, 2010).
NPV $39.91 $23.56 $17.71 $15.59 $30.26
Total $127.03
Constraints
The constraints of a linear programming model are the inequality that are used to define
the limitations on the decisions. In the case study constraints did arise due to the limited capital
resource of SoapMax limited. The table below summarises the limiting factors of the firm.
Year
A B C D E Total Available capital
0 $32.00 $10.00 $15.00 $8.00 $30.00 $95.00 <= $50.00
1 $10.00 $5.00 $7.00 $5.00 $12.00 $39.00 <= $29.00
2 $15.00 $5.00 $9.00 $6.00 $12.00 $47.00 <= $35.00
3 $14.00 $7.00 $12.00 $6.00 $11.00 $50.00 <= $40.00
4 $7.00 $5.00 $17.00 $29.00 <= $34.00
Investment opportunity
Expected cash outflows
From the table, we note that capital outflow needed every year for all the projects is beyond what
is available at the organization.
Results of the excel solver model
The problem was modelled and excel solver applied to derive optimal solution. The
results are as displayed in the tables below.
4
those that have been left out. The table below indicates the decision variables.
A B C D E
Selected 1 1 1 1 1
Opportunity
Objective function
This is the quantitative criteria that is of immediate importance to the firm. In this case
study the objective is to maximise the net present value of the firm for the four-year investment
period as indicated in the table below (Gass, 2010).
NPV $39.91 $23.56 $17.71 $15.59 $30.26
Total $127.03
Constraints
The constraints of a linear programming model are the inequality that are used to define
the limitations on the decisions. In the case study constraints did arise due to the limited capital
resource of SoapMax limited. The table below summarises the limiting factors of the firm.
Year
A B C D E Total Available capital
0 $32.00 $10.00 $15.00 $8.00 $30.00 $95.00 <= $50.00
1 $10.00 $5.00 $7.00 $5.00 $12.00 $39.00 <= $29.00
2 $15.00 $5.00 $9.00 $6.00 $12.00 $47.00 <= $35.00
3 $14.00 $7.00 $12.00 $6.00 $11.00 $50.00 <= $40.00
4 $7.00 $5.00 $17.00 $29.00 <= $34.00
Investment opportunity
Expected cash outflows
From the table, we note that capital outflow needed every year for all the projects is beyond what
is available at the organization.
Results of the excel solver model
The problem was modelled and excel solver applied to derive optimal solution. The
results are as displayed in the tables below.
4
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
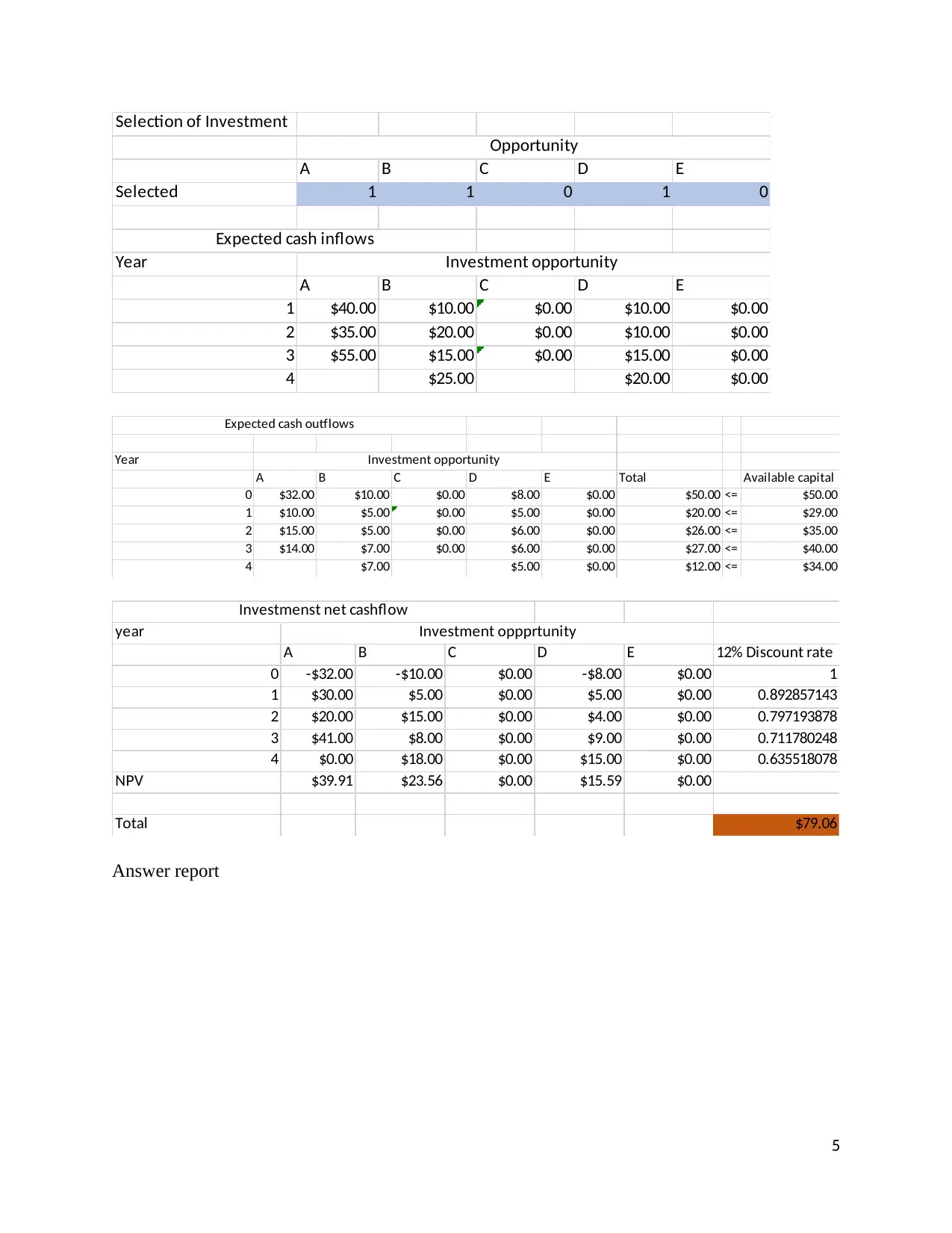
Selection of Investment
A B C D E
Selected 1 1 0 1 0
Year
A B C D E
1 $40.00 $10.00 $0.00 $10.00 $0.00
2 $35.00 $20.00 $0.00 $10.00 $0.00
3 $55.00 $15.00 $0.00 $15.00 $0.00
4 $25.00 $20.00 $0.00
Opportunity
Investment opportunity
Expected cash inflows
Year
A B C D E Total Available capital
0 $32.00 $10.00 $0.00 $8.00 $0.00 $50.00 <= $50.00
1 $10.00 $5.00 $0.00 $5.00 $0.00 $20.00 <= $29.00
2 $15.00 $5.00 $0.00 $6.00 $0.00 $26.00 <= $35.00
3 $14.00 $7.00 $0.00 $6.00 $0.00 $27.00 <= $40.00
4 $7.00 $5.00 $0.00 $12.00 <= $34.00
Investment opportunity
Expected cash outflows
year
A B C D E 12% Discount rate
0 -$32.00 -$10.00 $0.00 -$8.00 $0.00 1
1 $30.00 $5.00 $0.00 $5.00 $0.00 0.892857143
2 $20.00 $15.00 $0.00 $4.00 $0.00 0.797193878
3 $41.00 $8.00 $0.00 $9.00 $0.00 0.711780248
4 $0.00 $18.00 $0.00 $15.00 $0.00 0.635518078
NPV $39.91 $23.56 $0.00 $15.59 $0.00
Total $79.06
Investment oppprtunity
Investmenst net cashflow
Answer report
5
A B C D E
Selected 1 1 0 1 0
Year
A B C D E
1 $40.00 $10.00 $0.00 $10.00 $0.00
2 $35.00 $20.00 $0.00 $10.00 $0.00
3 $55.00 $15.00 $0.00 $15.00 $0.00
4 $25.00 $20.00 $0.00
Opportunity
Investment opportunity
Expected cash inflows
Year
A B C D E Total Available capital
0 $32.00 $10.00 $0.00 $8.00 $0.00 $50.00 <= $50.00
1 $10.00 $5.00 $0.00 $5.00 $0.00 $20.00 <= $29.00
2 $15.00 $5.00 $0.00 $6.00 $0.00 $26.00 <= $35.00
3 $14.00 $7.00 $0.00 $6.00 $0.00 $27.00 <= $40.00
4 $7.00 $5.00 $0.00 $12.00 <= $34.00
Investment opportunity
Expected cash outflows
year
A B C D E 12% Discount rate
0 -$32.00 -$10.00 $0.00 -$8.00 $0.00 1
1 $30.00 $5.00 $0.00 $5.00 $0.00 0.892857143
2 $20.00 $15.00 $0.00 $4.00 $0.00 0.797193878
3 $41.00 $8.00 $0.00 $9.00 $0.00 0.711780248
4 $0.00 $18.00 $0.00 $15.00 $0.00 0.635518078
NPV $39.91 $23.56 $0.00 $15.59 $0.00
Total $79.06
Investment oppprtunity
Investmenst net cashflow
Answer report
5
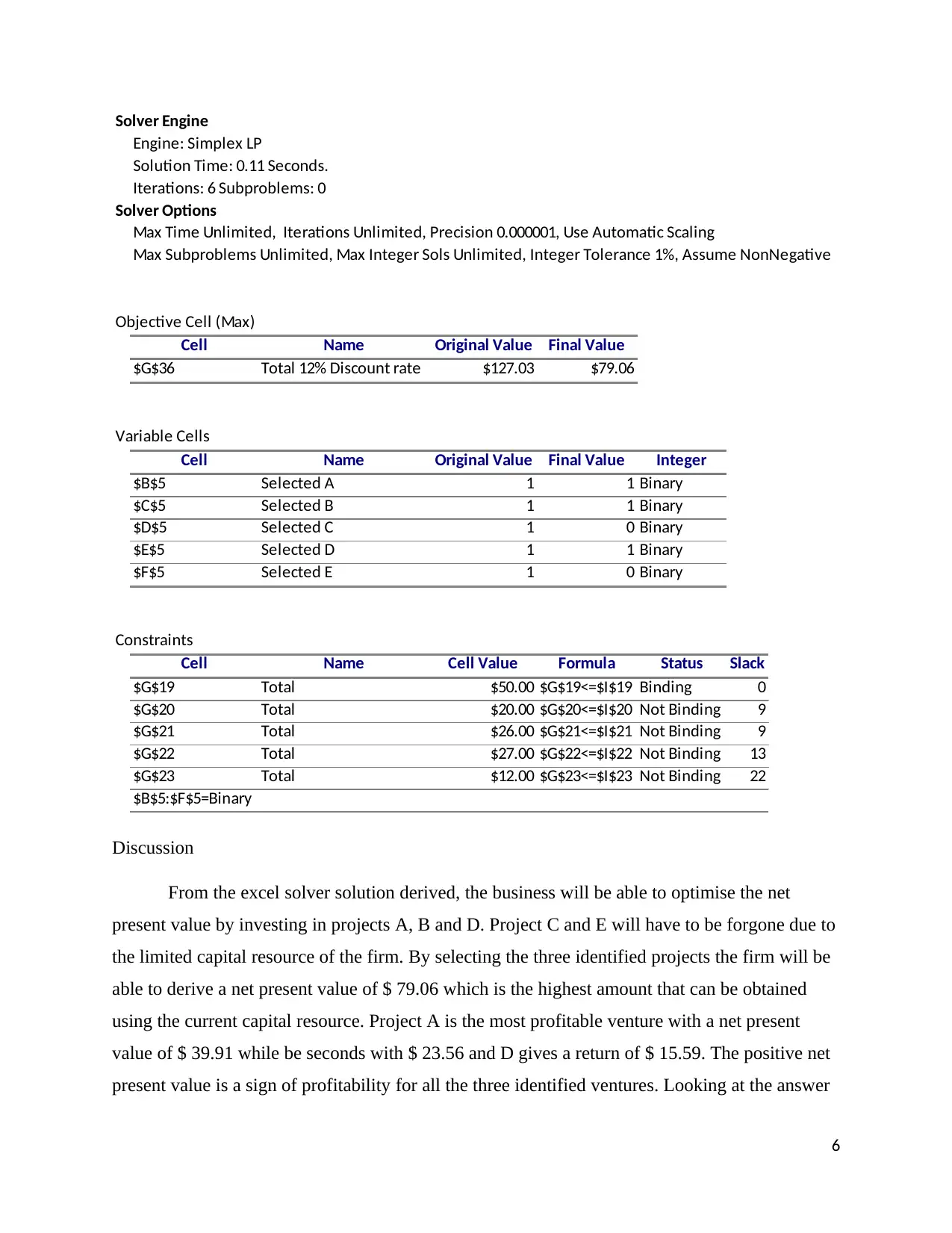
Solver Engine
Engine: Simplex LP
Solution Time: 0.11 Seconds.
Iterations: 6 Subproblems: 0
Solver Options
Max Time Unlimited, Iterations Unlimited, Precision 0.000001, Use Automatic Scaling
Max Subproblems Unlimited, Max Integer Sols Unlimited, Integer Tolerance 1%, Assume NonNegative
Objective Cell (Max)
Cell Name Original Value Final Value
$G$36 Total 12% Discount rate $127.03 $79.06
Variable Cells
Cell Name Original Value Final Value Integer
$B$5 Selected A 1 1 Binary
$C$5 Selected B 1 1 Binary
$D$5 Selected C 1 0 Binary
$E$5 Selected D 1 1 Binary
$F$5 Selected E 1 0 Binary
Constraints
Cell Name Cell Value Formula Status Slack
$G$19 Total $50.00 $G$19<=$I$19 Binding 0
$G$20 Total $20.00 $G$20<=$I$20 Not Binding 9
$G$21 Total $26.00 $G$21<=$I$21 Not Binding 9
$G$22 Total $27.00 $G$22<=$I$22 Not Binding 13
$G$23 Total $12.00 $G$23<=$I$23 Not Binding 22
$B$5:$F$5=Binary
Discussion
From the excel solver solution derived, the business will be able to optimise the net
present value by investing in projects A, B and D. Project C and E will have to be forgone due to
the limited capital resource of the firm. By selecting the three identified projects the firm will be
able to derive a net present value of $ 79.06 which is the highest amount that can be obtained
using the current capital resource. Project A is the most profitable venture with a net present
value of $ 39.91 while be seconds with $ 23.56 and D gives a return of $ 15.59. The positive net
present value is a sign of profitability for all the three identified ventures. Looking at the answer
6
Engine: Simplex LP
Solution Time: 0.11 Seconds.
Iterations: 6 Subproblems: 0
Solver Options
Max Time Unlimited, Iterations Unlimited, Precision 0.000001, Use Automatic Scaling
Max Subproblems Unlimited, Max Integer Sols Unlimited, Integer Tolerance 1%, Assume NonNegative
Objective Cell (Max)
Cell Name Original Value Final Value
$G$36 Total 12% Discount rate $127.03 $79.06
Variable Cells
Cell Name Original Value Final Value Integer
$B$5 Selected A 1 1 Binary
$C$5 Selected B 1 1 Binary
$D$5 Selected C 1 0 Binary
$E$5 Selected D 1 1 Binary
$F$5 Selected E 1 0 Binary
Constraints
Cell Name Cell Value Formula Status Slack
$G$19 Total $50.00 $G$19<=$I$19 Binding 0
$G$20 Total $20.00 $G$20<=$I$20 Not Binding 9
$G$21 Total $26.00 $G$21<=$I$21 Not Binding 9
$G$22 Total $27.00 $G$22<=$I$22 Not Binding 13
$G$23 Total $12.00 $G$23<=$I$23 Not Binding 22
$B$5:$F$5=Binary
Discussion
From the excel solver solution derived, the business will be able to optimise the net
present value by investing in projects A, B and D. Project C and E will have to be forgone due to
the limited capital resource of the firm. By selecting the three identified projects the firm will be
able to derive a net present value of $ 79.06 which is the highest amount that can be obtained
using the current capital resource. Project A is the most profitable venture with a net present
value of $ 39.91 while be seconds with $ 23.56 and D gives a return of $ 15.59. The positive net
present value is a sign of profitability for all the three identified ventures. Looking at the answer
6
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

report, the binding constraints are those that have been fully utilised. The initial capital available
at the start of the investment was fully allocated for the three projects. For the subsequent years 1
to 4, the business did use just a portion of the available capital which is defined by the not
Binding term of the answer report. The total cost of financing the projects for year one and two
can increase by a maximum of $9 for each year while for year 3 and 4 the total cost can increase
by $13 and $22 respectively without the firm having to look for additional capital funding for the
projects.
Conclusion
Decision making is the core of efficient running of an organization. To ensure effective,
fast and reliable decisions, linear programming concept can be applied in several business
scenarios to assist the mangers settle for the best choice of action. In this report the objective is
to illustrate how linear programming can be applied to solve a real-world problem. A case study
of SoapMax did indicate that by applying linear programming a firm is able to settle on the best
investment opportunity and hence optimize the net present value.
7
at the start of the investment was fully allocated for the three projects. For the subsequent years 1
to 4, the business did use just a portion of the available capital which is defined by the not
Binding term of the answer report. The total cost of financing the projects for year one and two
can increase by a maximum of $9 for each year while for year 3 and 4 the total cost can increase
by $13 and $22 respectively without the firm having to look for additional capital funding for the
projects.
Conclusion
Decision making is the core of efficient running of an organization. To ensure effective,
fast and reliable decisions, linear programming concept can be applied in several business
scenarios to assist the mangers settle for the best choice of action. In this report the objective is
to illustrate how linear programming can be applied to solve a real-world problem. A case study
of SoapMax did indicate that by applying linear programming a firm is able to settle on the best
investment opportunity and hence optimize the net present value.
7
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

References
Chanda, R. S., 2013. ON Fuzzy Linear Programming Technique Application. International Journal for
Scientific Research & Development, 1(4), pp. 2321-0613 .
Edem, O. P., Amade, B. & Ononuju, C., 2014. Application of Linear Programming to Production
Systems Problem. International Journal of Management Sciences and Business Research, 3(10),
pp. 2226-8235.
Gass, S. I., 2010. Linear Programming: Methods and Applications, New York : Dover Publications.
Veselovska, L., 2013. Process Of Development Of Model Based On Linear Programming To Solve
Resource Allocation Tasks With Emphasis On Financial Aspects. European Scientific Journal,
Volume 1, p. 1857 – 7881.
8
Chanda, R. S., 2013. ON Fuzzy Linear Programming Technique Application. International Journal for
Scientific Research & Development, 1(4), pp. 2321-0613 .
Edem, O. P., Amade, B. & Ononuju, C., 2014. Application of Linear Programming to Production
Systems Problem. International Journal of Management Sciences and Business Research, 3(10),
pp. 2226-8235.
Gass, S. I., 2010. Linear Programming: Methods and Applications, New York : Dover Publications.
Veselovska, L., 2013. Process Of Development Of Model Based On Linear Programming To Solve
Resource Allocation Tasks With Emphasis On Financial Aspects. European Scientific Journal,
Volume 1, p. 1857 – 7881.
8
1 out of 8
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





