MCV4U Calculus Unit 1: Rates of Change Assessment of Learning Solution

This document presents a comprehensive solution to a Calculus assignment, specifically focusing on the topic of rates of change. The solution addresses a range of problems, starting with the calculation of the average rate of change of a function over a given interval. It then delves into finding the instantaneous rate of change and the derivative of a function at a specific point, highlighting their relationship. The solution also explains the difference between secant and tangent lines and how they relate to the rate of change, including illustrative sketches. Furthermore, the assignment covers problems related to limits, including evaluating limits and understanding their meaning, and finding the slope of a tangent line. The solution also includes questions on finding the derivative of a function using first principles and determining the equation of a tangent line. Finally, the assignment concludes with a problem that involves finding the point on a parabola where the tangent line is parallel to a given line.

Running head: CALCULUS
CALCULUS
Name of the Student
Name of the University
Author Note

1CALCULUS
1. Determine the average rate of change of y in the function y=2 x3 +7 x2 +2 x−3 over the
interval [3, 5].
Solution: The Average rate of change of any function ‘y’ with respect to x is given by the
= change∈ y
chnage∈ x = ∆ y
∆ x = y2− y1
x2−x1
In this scenario x2 and x1 is given which are 5 and 3 respectively. For x2 find y2 and for x1 find y1.
Case 1: x2 = 5
¿> y =2 ( 5 ) 3+ 7 ( 52 ) +2 ( 5 ) −3
¿> y =250+175+10−3=432
So y2=432.
Case 2: x1 = 3
¿> y =2 (3 )3+ 7 ( 32 ) +2 ( 3 )−3
¿> y =54+63+6−3=120
So y1=120.
∴ Average rate of change of the function = y2− y1
x2−x1
= 432−120
5−3 = 312
2 = 156 Ans.
2. Given the function f (x)=2 x2 +3 x+1 ,
a. Find the instantaneous rate of change when x = 1.
Solution: For a function, Instantaneous rate of change at a point is the same as the slope of the
tangent line.
The expression for the IROC is given by, f ' ( x ) =lim
h →0
f ( x+ h ) −f ( x )
h
¿> f ' ( x )=lim
h → 0
{2 ( x+h )2+ 3 ( x +h )+1−(2 x2+3 x +1)}
h
¿>f ' ( x )=lim
h → 0
2 x2 +4 xh+ 2 h2+3 x +3 h+1−2 x2−3 x−1
h

2CALCULUS
¿> f ' ( x ) =lim
h → 0
4 xh+ 2h2 +3 h
h
¿> f ' ( x ) =lim
h → 0
h( 4 x+2h+3)
h
¿> f ' ( x )=lim
h → 0
4 x+2 h+3
As h →0, the equation will become,
¿> f ' ( x ) =4 x +3
And at x= 1,
¿> f ' ( x )=4 × 1+ 3=7 Ans .
b. Find the value of the derivative when x = 1.
Solution: find the derivative first,
¿> f ( x )=2 x2 +3 x +1
¿> f ' (x )=2 ×2 x2−1 +3 ×1 x1−1
¿> f ' ( x ) =4 x +3
At x= 1,
¿> f ' ( x )=4 × 1+ 3=7 Ans .
c. What did you notice?
Solution: It is noticed that the first order derivative and instantaneous rate of change of a
equation at same point x, is same. It can be said that the first order derivative will give the IROC
of equation and the IROC provides the slope of the tangent line over the equation.
3. Explain the difference between a secant line and a tangent line. How do they relate to the
rate of change of a function? Include a sketch of each type of line in your solution.

3CALCULUS
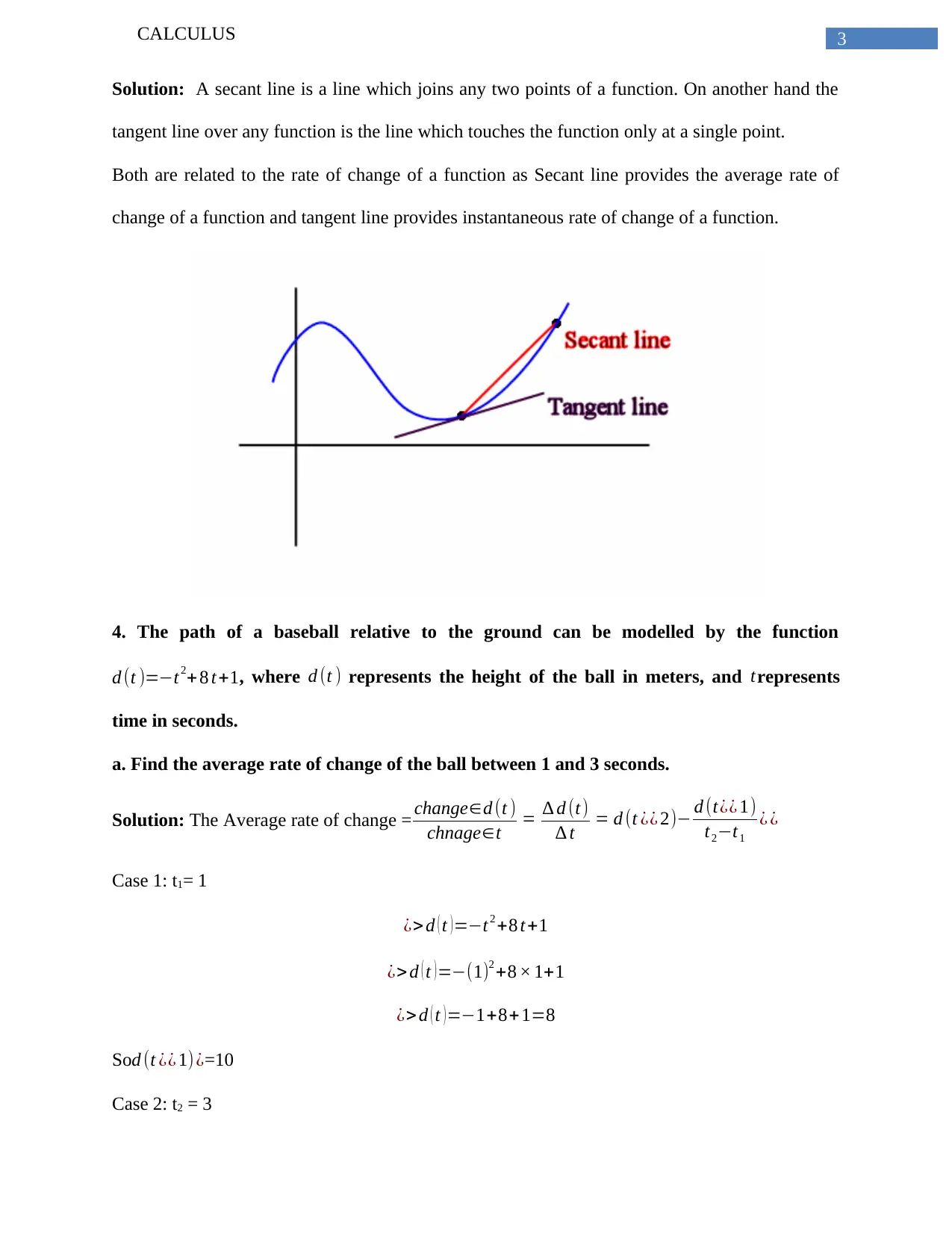
Solution: A secant line is a line which joins any two points of a function. On another hand the
tangent line over any function is the line which touches the function only at a single point.
Both are related to the rate of change of a function as Secant line provides the average rate of
change of a function and tangent line provides instantaneous rate of change of a function.
4. The path of a baseball relative to the ground can be modelled by the function
d (t )=−t2+ 8 t+1, where d (t ) represents the height of the ball in meters, and trepresents
time in seconds.
a. Find the average rate of change of the ball between 1 and 3 seconds.
Solution: The Average rate of change = change∈d (t )
chnage∈t = ∆ d (t)
∆ t = d (t ¿¿ 2)− d (t¿¿ 1)
t2−t1
¿ ¿
Case 1: t1= 1
¿> d ( t )=−t2 +8 t+1
¿> d ( t )=−(1)2 +8 × 1+1
¿> d ( t ) =−1+8+1=8
Sod (t ¿¿ 1)¿=10
Case 2: t2 = 3

4CALCULUS
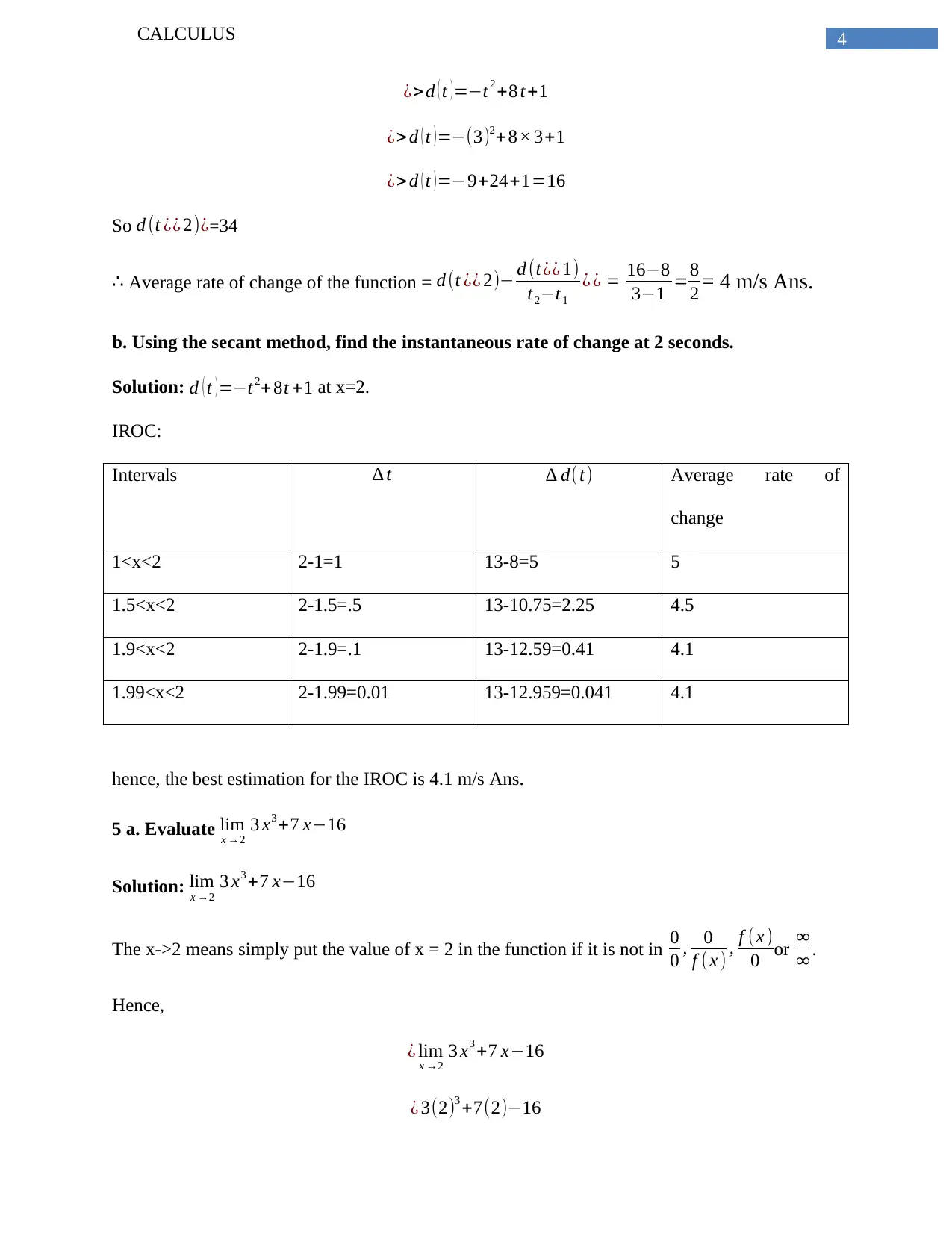
¿> d ( t )=−t2 +8 t+1
¿> d ( t )=−(3)2+8× 3+1
¿> d ( t )=−9+24+1=16
So d (t ¿¿ 2)¿=34
∴ Average rate of change of the function = d (t ¿¿ 2)− d (t¿¿ 1)
t2−t1
¿ ¿ = 16−8
3−1 =8
2 = 4 m/s Ans.
b. Using the secant method, find the instantaneous rate of change at 2 seconds.
Solution: d ( t )=−t2+ 8t +1 at x=2.
IROC:
Intervals ∆ t ∆ d(t) Average rate of
change
1<x<2 2-1=1 13-8=5 5
1.5<x<2 2-1.5=.5 13-10.75=2.25 4.5
1.9<x<2 2-1.9=.1 13-12.59=0.41 4.1
1.99<x<2 2-1.99=0.01 13-12.959=0.041 4.1
hence, the best estimation for the IROC is 4.1 m/s Ans.
5 a. Evaluate lim
x →2
3 x3 +7 x−16
Solution: lim
x →2
3 x3 +7 x−16
The x->2 means simply put the value of x = 2 in the function if it is not in 0
0 , 0
f ( x ) , f (x )
0 or ∞
∞ .
Hence,
¿ lim
x →2
3 x3 +7 x−16
¿ 3(2)3 +7(2)−16

5CALCULUS
¿ 3 ×8+7 × 2−16=22 Ans .
b. What is the meaning of this value?
Solution: The meaning of this value of limit is the value of equation 3 x3+7 x −16 at x = 2 which
is given.
6. Evaluate the following limits.
a. lim
x→ 4
x2−16
x−4
Solution: In current scenario, x tends to 4 in which the limit gives f ( x )
0 ,
To solve this, the x from the denominator has to be eliminated.
¿ lim
x→ 4
¿ ¿¿ { ∴ use formula ( a2−b2 ) =(a+b)(a−b) }
¿ lim
x→ 4
( x−4)( x+4)
x−4
¿ lim
x→ 4
x + 4=4 +4=8 Ans .
b. lim
x→ ∞
8 x3−5 x2+ 17
6 x3 +2 x2−4 x
Solution: This limit is in form of ∞
∞ ,
∴ using L−hospitalrule ¿ solve this .
¿ lim
x→ ∞
8 x3−5 x2+ 17
6 x3 +2 x2−4 x
¿ lim
x→ ∞
24 x2−10 x
18 x2 +4 x
¿ lim
x→ ∞
48 x
36 x = 4
3 Ans .
c. lim
h→ 0
√ 49+ h−7
h

6CALCULUS
Solution: Following limit is in f (x )
0 form .
To solve this, it has to be rationalized.
¿ lim
h→ 0
√ 49+h−7
h × √ 49+h+7
√ 49+h+7
¿ lim
h→ 0
( √49+h)2−(7)2
h √49+ h+7
¿ lim
h→ 0
( √49+h)2−(7)2
h √49+ h+7
¿ lim
h→ 0
49+h−49
h √ 49+ h+7
¿ lim
h→ 0
h
h √ 49+ h+7
¿ lim
h→ 0
1
√49+ h+7 = 1
√49+7 = 1
7+7 = 1
14 Ans .
d. lim
y → 2
y3−8
2 y2−7 y +12
Solution: The given limit is in form of 0
f ( x ),
∴ lim
y →2
y3−8
2 y2−7 y +12
¿ lim
y →2
( y−2 ) ( y2 +2 y +4 )
2 y2−7 y +12

7CALCULUS
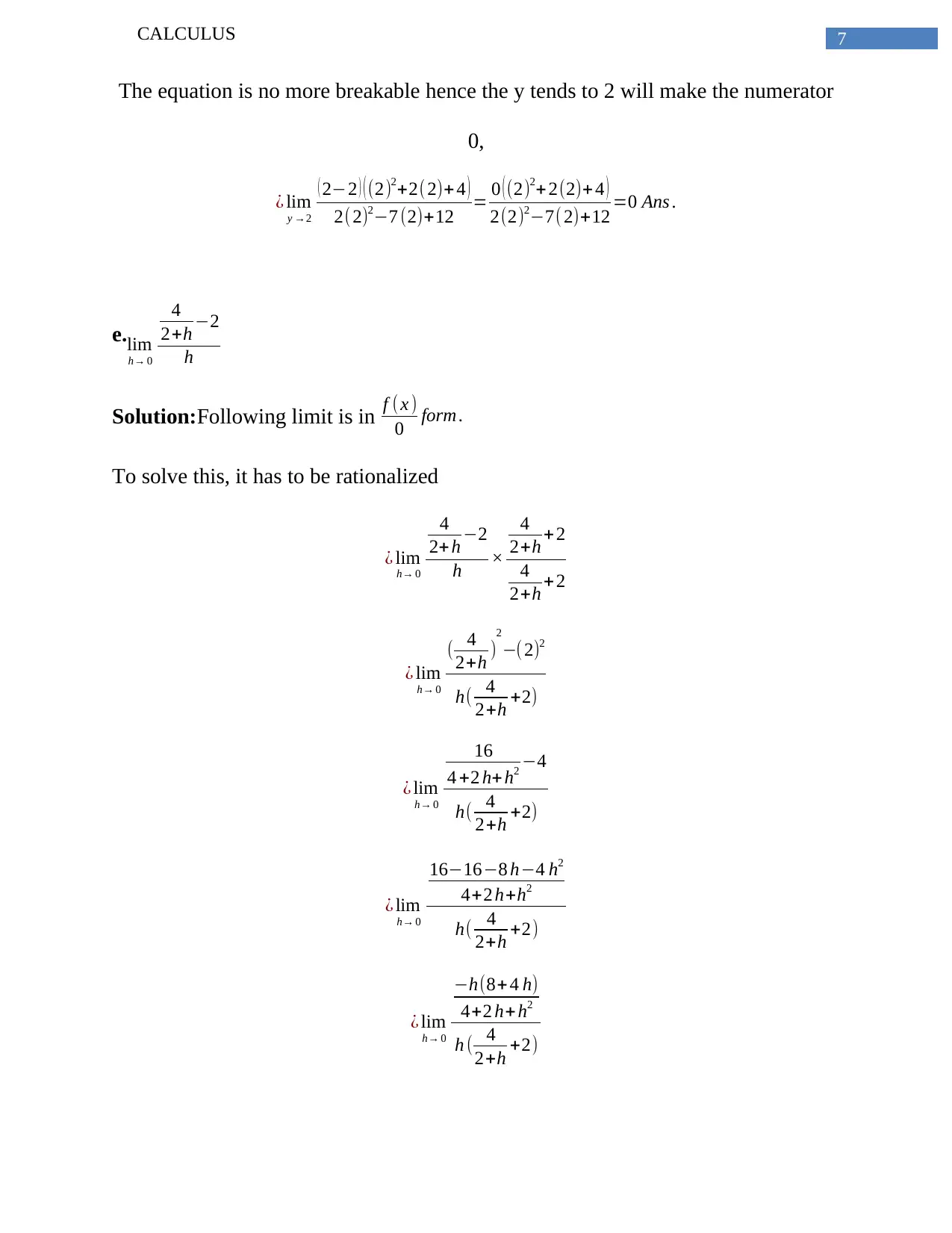
The equation is no more breakable hence the y tends to 2 will make the numerator
0,
¿ lim
y →2
( 2−2 ) ( (2)2+2( 2)+ 4 )
2( 2)2−7 (2)+12 = 0 ( (2)2+ 2(2)+ 4 )
2(2)2−7( 2)+12 =0 Ans .
e.lim
h→ 0
4
2+h −2
h
Solution:Following limit is in f (x )
0 form .
To solve this, it has to be rationalized
¿ lim
h→ 0
4
2+ h −2
h ×
4
2+h +2
4
2+h +2
¿ lim
h→ 0
( 4
2+h )
2
−(2)2
h( 4
2+h +2)
¿ lim
h→ 0
16
4 +2 h+ h2 −4
h( 4
2+h +2)
¿ lim
h→ 0
16−16−8 h−4 h2
4+2 h+h2
h( 4
2+h +2)
¿ lim
h→ 0
−h(8+ 4 h)
4+2 h+h2
h ( 4
2+h +2)

8CALCULUS
¿ lim
h→ 0
−h (8+4 h)
4 +2 h+h2 × 1
h( 4
2+h +2)
¿ lim
h→ 0
−(8+4 h)
4+2 h+h2 × 1
( 4
2+ h +2)
¿ lim
h→ 0
−(8+ 4 × 0)
4+2 ×0+02 × 1
( 4
2+0 +2)
¿ lim
h→ 0
−8
4 × 1
4 =−1
2 Ans .
7. Find the slope of the tangent line at point (-2,2) on the curve f ( x )=2 x2+ 3 x
Solution: The slope of the tangent line for f(x) is given by f’(x).
Hence, the point given is (-2,2) where x = -2, y 2, and f ( x )=2 x2+3 x
¿> f ' ( x ) =4 x +3
at x = -2,
¿>f ' ( x )=4 × (−2 ) +3=−5 Ans .
∴ the slope of thetangent line is−5.
8. Find the derivative of the function f (x)=x2 −10 x +3 using First Principles.
Solution: First Principle is given by, f ' ( x )=lim
h →0
f ( x+h )−f ( x )
h
f (x)=x2 −10 x +3
and
f ( x+ h)= ( x+ h ) 2−10(x +h)+3
f ( x +h )=x2+ h2+ 2 xh−10 x −10 h+3

9CALCULUS
¿ lim
h→ 0
f ( x +h ) −f ( x )
h
¿ lim
h→ 0
x2+ h2 +2 xh−10 x−10 h+3−x2 +10 x−3
h
¿ lim
h→ 0
h(h+2 x −10)
h
¿ lim
h→ 0
( h+2 x −10 )=0+ 2 x−10=2 x −10 Ans .
9. Find the equation of the tangent line at point (2,2) on the curve f (x)=x2 −7 x +12.
Solution: first find the slope of the line,
f ' ( x )=2 x−7.
at x = 2,
f ' ( 2 )=2 ×2−7=−3
Now using slope intercept formula find the value of c,
¿> y =mx+c
¿>2=(−3)2+c
¿> c=8
Hence, the equation will be,
¿> y =mx+c
¿> y =−3 x+ 8 Ans .
10. At what point on the parabola y=3 x2 +2 x is the tangent line parallel to the line y = 10x
−2?
Solution: The given line is parallel to the tangent line, hence the slope of the line will be equal to
the slope of the tangent line.
Using slope intercept formula comparing line equation wit y=mx+c
the slop (m) is 10.

10CALCULUS
According to the question,
the first order derivative of the parabola should be equal to 10.
¿> dy
dx =10
¿> d (3 x2+ 2 x )
dx =10
¿>6 x +2=10
¿> x= 4
3 ,
Now put the value of x in equation of parabola.
 y=3 ×( 4
3 )
2
+2( 4
3 )
 y= 16
3 + 8
3 = 24
3 =8.
∴ hence the points are ( 4
3 , 8 ) Ans .