MCV4U Unit 1 Assessment, Part 2: Calculus and Function Analysis

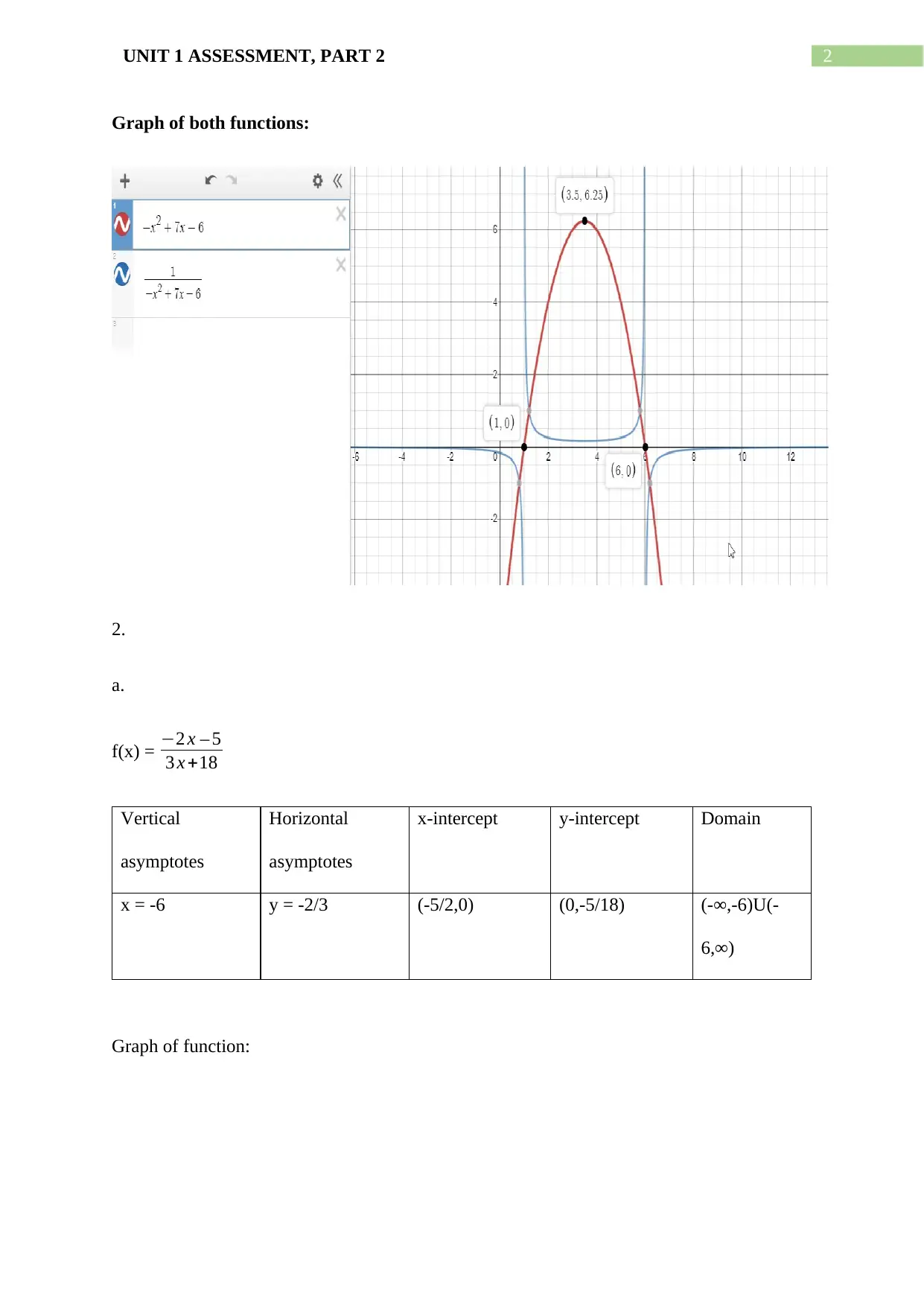
This document provides a detailed solution to the MCV4U Unit 1 Assessment, Part 2. The solution covers a range of calculus concepts, including analyzing functions, finding zeroes, determining maxima and minima, and sketching graphs of functions and their reciprocals. It addresses rational equations, inequalities, and solving for real roots. The assignment also includes problems involving derivatives and evaluating them, finding positive and negative intervals of functions, and solving for dimensions of a box with a given volume. The solutions are presented with step-by-step calculations and explanations to aid understanding. This resource is designed to help students grasp key calculus concepts and improve their problem-solving skills. The document is a valuable resource for students seeking to understand and solve complex mathematical problems.

Running head: UNIT 1 ASSESSMENT, PART 2
UNIT 1 ASSESSMENT, PART 2
Name of the Student
Name of the University
Author Note

1UNIT 1 ASSESSMENT, PART 2
1.
Given f(x) = -x^2 + 7x – 6
zeroes => -x^2 + 7x – 6 = 0
 x^2 - 7x + 6 = 0
 x^2 – 6x – x + 6 = 0
 (x-1)(x-6) = 0
 x = 1 and 6
maxima and minima => f’(x) = 0
 -2x + 7= 0
 x = 3.5
at x = 3.5 f’’(3.5) = -2 <0 (hence, x = 3.5 is maximum)
at f(3.5) = 6.25
x domain = (-∞,∞)
y range = (-∞,6.25]
The function is a parabola with shifted y axis at x = 3.5.
Reciprocal of f(x) = g(x) = 1/(-x^2 + 7x – 6)
Domain => -x^2 + 7x – 6 ≠0
 x ≠ 1 or 6.
Vertical asymptotes x = 1 x = 6.

2UNIT 1 ASSESSMENT, PART 2
Graph of both functions:
2.
a.
f(x) = −2 x – 5
3 x +18
Vertical
asymptotes
Horizontal
asymptotes
x-intercept y-intercept Domain
x = -6 y = -2/3 (-5/2,0) (0,-5/18) (-∞,-6)U(-
6,∞)
Graph of function:

3UNIT 1 ASSESSMENT, PART 2
b.
f(x) = −2 x – 5
3 x +18
From the graph of the function it can be seen that function is negative in (-∞,-6) U (-2.5,∞)
and positive in (-6,-2.5).
Hence, positive interval = (-6,-2.5)
Negative interval = (-∞,-6) U (-2.5,∞)
3.
−7 x
9 x+11 – 12= 1
x
=> −7 x−12(9 x+ 11)
9 x +11 = 1
x

4UNIT 1 ASSESSMENT, PART 2
=> −7 x2−12 x ( 9 x+11 )=9 x +11
=> −7 x2−108 x2−132=9 x +11
=> −115 x2−9 x−143=0
=> 115 x2+ 9 x +143=0
x = −9 ± √ 81−4∗115∗143
2∗115
As √81−4∗115∗143 < 0 hence the roots are not real.
Hence, there are no real roots of the equation.
b.
x−1
x+ 2 = 3 x +8
5 x−1
 (x−1)(5 x−1) = (3 x+ 8)( x+2)
 5 x2−x−5 x+1=3 x2 +16 x +8 x+ 16
 2 x2 −30 x −15=0
x = 30± √900+ 4∗15∗2
2∗2 = 15.484 and -0.484.
4.
8x-3 <= 2x+1 <= 17x-8
 6x-4 <= 0 <= 17x-8
 6x – 4 <= 0 and 17x-8 >= 0
 x <= 2/3 and x >= 8/17
 8/17<=x <=2/3

5UNIT 1 ASSESSMENT, PART 2
-∞ 0 ∞
x
-5/9
5.
5 x +4
x−1 <5 x−7
x+13
 (5x+4)(x+13) < (5x-7)(x-1)
 5x^2 + 65x + 4x + 52 < 5x^2 – 5x – 7x + 7
 81x < -45
 x < -5/9
Interval chart:
6.
Given length = 3 cm, breath = 5 cm and height = 7 cm
By the question,
(3+x)(5+x)(7+x) = 693 cm^3
 (15+8x+x^2)(7+x) = 693
 105 + 56x + 7x^2 + 15x + 8x^2 + x^3 = 693

6UNIT 1 ASSESSMENT, PART 2
 x^3 + 15x^2 + 71x -588 = 0
The only real root of the equation is x = 4 and hence the dimensions of the box must be
increased by 4 cm such that the volume is 693 cm^3.
7.
Let width of container is w.
Hence, length l = 3w + 1.
Height h = 2w -5
Thus by the question,
w*(3w+1)*(2w-5) >= 8436
 w*(6w^2-13w-5) = 8436
 6w^3 -13w^2-5w -8436 >=0
Now, the real root of the equality is w = 12
Hence, w >= 12 meters
Length l >= 3*12 +1 => l >= 37 meters.
Height h >= 2*12 -5 >= 19 meters.