ME5112 Math Assessment: Applying Mathematical Concepts and Methods
VerifiedAdded on 2023/04/21
|12
|2189
|244
Homework Assignment
AI Summary
This document presents a comprehensive solution to a mathematics assessment, covering a range of topics including solving differential equations, applying Maclaurin and Taylor series for approximations, calculating eigenvalues and eigenvectors of a matrix, and using Euler's method to approximate solutions to differential equations related to Newton's law of cooling. The solution also includes graphical analysis of pressure and volume data, numerical integration using Simpson's and Trapezium rules, and an application of Torricelli's law to determine the emptying time of a tank. Each problem is addressed with detailed steps and explanations, providing a thorough understanding of the mathematical concepts and methods involved.

ME5112 Math’s Assessment
Student Name
Institution
Date of Submission
Student Name
Institution
Date of Submission
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

1. Solving the differential equation
i.
y dy
dx − ( 1+ y2 ) x2=0
dy
dx = ( 1+ y2 ) x2
y
ii. dx
dt − x
t−1 =t2−1
dx
dt =t2−1+ x
t−1
When t >1
dx
dt > ( 2−1 )+ x
2−1
Hence dx
dt >0
2. Using the Maclaurin series
In this problem will apply the first four non-zero terms of the McLaurin’s series to
approximate f ( x ) =ln (1+2 x) and thereafter obtain the value of f ( 1.2 )to 4 decimal
places
The McLaurin’s series formula is given as;
f ( 0 )+ f '(0)
1 ! x + f ' '(0)
2! x2 + f ' ' ' (0)
3! x3+ f iv (0)
4 ! x4 … f n ( 0 )
n! xn
f ( x )=ln (1+2 x)
f ( 0 )=ln ( 1+2∗0 )=ln (1 )=0
f i ( x )= d
dx ln ( 1+2 x )= 2
1+ 2 x
f i ( 0 )= 2
1+ 2 x =2
f ii ( x ) = d
dx f i ( x )
f ii ( x ) = d
dx
2
1+2 x = −4
( 1+2 x ) 2
i.
y dy
dx − ( 1+ y2 ) x2=0
dy
dx = ( 1+ y2 ) x2
y
ii. dx
dt − x
t−1 =t2−1
dx
dt =t2−1+ x
t−1
When t >1
dx
dt > ( 2−1 )+ x
2−1
Hence dx
dt >0
2. Using the Maclaurin series
In this problem will apply the first four non-zero terms of the McLaurin’s series to
approximate f ( x ) =ln (1+2 x) and thereafter obtain the value of f ( 1.2 )to 4 decimal
places
The McLaurin’s series formula is given as;
f ( 0 )+ f '(0)
1 ! x + f ' '(0)
2! x2 + f ' ' ' (0)
3! x3+ f iv (0)
4 ! x4 … f n ( 0 )
n! xn
f ( x )=ln (1+2 x)
f ( 0 )=ln ( 1+2∗0 )=ln (1 )=0
f i ( x )= d
dx ln ( 1+2 x )= 2
1+ 2 x
f i ( 0 )= 2
1+ 2 x =2
f ii ( x ) = d
dx f i ( x )
f ii ( x ) = d
dx
2
1+2 x = −4
( 1+2 x ) 2

f ii ( 0 ) = 4
( 1+2∗0 )2 =−4
f iii ( x ) = d
dx
−4
( 1+2 x )2 = 16
( 1+2 x ) 2
f iii ( 0 )= 16
( 1+2∗0 )2 =16
f iv ( x ) = d
dx
16
( 1+2 x ) 2 = −96
( 1+2 x ) 4
f iv ( 0 )= −96
( 1+2∗0 )4 =−96
Now replacing the values in the series expansion formula we obtain
f ( 0 ) + f ' (0)
1 ! x + f ' '( 0)
2! x2 + f ' ' ' (0)
3! x3+ f iv( 0)
4 ! x4=0+ 2
1 ! x− 4
2 ! x2 + 16
3 ! x3− 96
4 x4
¿ 2 x−2 x2 + 8
3 x3−4 x4
this is theMcLaurin’s series expansion of
f ( x )=ln (1+2 x)
At f ( 1.2 ) we have 2 ( 1.2 ) −2 ( 1.2 ) 2 + 8
3 ( 1.2 ) 3−4 ( 1.2 ) 4 =−4.166
3. Taylor’s series
Using the first 5 terms of the Taylors series to estimate the value of
f ( 1.1 ) ¿ 2 decimal Places.
The formula is given by:
f ( x ) =f ( a)+ f ' ( a )
1! ( x−a)+ f ' ' (a)
2 ! (x−a)2 + f ' ' '(a)
3 ! (x−a)3 + f iv (a)
4 ! ( x−a)4 … f n ( a )
n ! ( x −a)n ¿
For the given problem the value of a is 1with this the above formula can be expressed as
f ( x )=f (1)+ f ' (1 )
1! (x−1)+ f ' '(1)
2 ! ( x−1)2 + f ' ' ' (1)
3 ! ( x−1)3+ f iv (1)
4 ! ( x −1)4 … f n ( 1 )
n ! ( x−1)n ¿
Now
( 1+2∗0 )2 =−4
f iii ( x ) = d
dx
−4
( 1+2 x )2 = 16
( 1+2 x ) 2
f iii ( 0 )= 16
( 1+2∗0 )2 =16
f iv ( x ) = d
dx
16
( 1+2 x ) 2 = −96
( 1+2 x ) 4
f iv ( 0 )= −96
( 1+2∗0 )4 =−96
Now replacing the values in the series expansion formula we obtain
f ( 0 ) + f ' (0)
1 ! x + f ' '( 0)
2! x2 + f ' ' ' (0)
3! x3+ f iv( 0)
4 ! x4=0+ 2
1 ! x− 4
2 ! x2 + 16
3 ! x3− 96
4 x4
¿ 2 x−2 x2 + 8
3 x3−4 x4
this is theMcLaurin’s series expansion of
f ( x )=ln (1+2 x)
At f ( 1.2 ) we have 2 ( 1.2 ) −2 ( 1.2 ) 2 + 8
3 ( 1.2 ) 3−4 ( 1.2 ) 4 =−4.166
3. Taylor’s series
Using the first 5 terms of the Taylors series to estimate the value of
f ( 1.1 ) ¿ 2 decimal Places.
The formula is given by:
f ( x ) =f ( a)+ f ' ( a )
1! ( x−a)+ f ' ' (a)
2 ! (x−a)2 + f ' ' '(a)
3 ! (x−a)3 + f iv (a)
4 ! ( x−a)4 … f n ( a )
n ! ( x −a)n ¿
For the given problem the value of a is 1with this the above formula can be expressed as
f ( x )=f (1)+ f ' (1 )
1! (x−1)+ f ' '(1)
2 ! ( x−1)2 + f ' ' ' (1)
3 ! ( x−1)3+ f iv (1)
4 ! ( x −1)4 … f n ( 1 )
n ! ( x−1)n ¿
Now
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

f ( a )=f ( 1 )=1
1 =1
f ' ( a )=f ' ( 1 )= d
dx x−1=−1 x−2=−1
f ' ' ( a ) =f ' ' ¿
f '' ' ( a )=f ' '' (1 )= d
dx (2 x−3 ) =−6 x−4 =−6
f iv ( a ) =f iv ( 1 ) = d
dx (−6 x−4 ) =24 x−5=24
Replacing the obtained values in the previously stated formula gives
f ( x )=1− 1
1 ! ( x−1 ) + 2
2 ! ( x−1 )2− 6
3 ! ( x −1)3 + 24
4 ! ( x−1)4
which can Be simplified to
1− ( x−1 ) + ( x −1 ) 2− ( x−1 ) 3 + ( x−1 ) 4
This is the Taylor’s series expansion
Now obtaining
f ( 1.1 ) =1− ( 1.1−1 ) + ( 1.1−1 )2− ( 1.1−1 )3 + ( 1.1−1 ) 4
¿ 1−1.1+0.12 −0.13+ 0.14=0.9091
4. Integral
i.
∫
0
1
1
1+ x2 =¿∫
0
1
( 1+ x2 ) −1
¿
Let u=1+ x2
Then ∫
0
1
u−1 dx
du
dx =2 x
dx= du
2 x
1 =1
f ' ( a )=f ' ( 1 )= d
dx x−1=−1 x−2=−1
f ' ' ( a ) =f ' ' ¿
f '' ' ( a )=f ' '' (1 )= d
dx (2 x−3 ) =−6 x−4 =−6
f iv ( a ) =f iv ( 1 ) = d
dx (−6 x−4 ) =24 x−5=24
Replacing the obtained values in the previously stated formula gives
f ( x )=1− 1
1 ! ( x−1 ) + 2
2 ! ( x−1 )2− 6
3 ! ( x −1)3 + 24
4 ! ( x−1)4
which can Be simplified to
1− ( x−1 ) + ( x −1 ) 2− ( x−1 ) 3 + ( x−1 ) 4
This is the Taylor’s series expansion
Now obtaining
f ( 1.1 ) =1− ( 1.1−1 ) + ( 1.1−1 )2− ( 1.1−1 )3 + ( 1.1−1 ) 4
¿ 1−1.1+0.12 −0.13+ 0.14=0.9091
4. Integral
i.
∫
0
1
1
1+ x2 =¿∫
0
1
( 1+ x2 ) −1
¿
Let u=1+ x2
Then ∫
0
1
u−1 dx
du
dx =2 x
dx= du
2 x
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

¿
∫
0
1
( u )−1∗1
2 x du=∫
0
1 1
u ∗1
2 x du= 1
2 x lnu
¿ 1
2 ln ( 1+12 )= π
4
ii) Binomial series
f ( x )= 1
1+ x2
The formula is stated as
( 1+x ) k=1+kx + k ( k −1 )
2 ! x2+ k ( k −1 ) ( k−2 )
3 ! x3
k =2
5. Eigenvalues and eigenvectors
A=[6 2
2 3]
Eigenvlues
Given A to be a square matrix, v a vector and λ is a scalr tht satisfy the formula Av=λv .
λ Is defines as the eigenvalue with eigenvector v of A.
hence theEigenvalues of will be obtained from the roots of the equation det ( A−λI ) =0
Hence
det ( (6 2
2 3 )−λ (1 0
0 1) ): λ2−9 λ+14
Solving for λ2−9 λ+14=0
Using the quadratic equation we obtain the values of λ as 2nd 7
This are the eigenvalues of matrix A
Eigenvectors
Being that A is a square matrix, v vector and λa scalar satisfying the eqution Av=λv ,
therefore v is an eigenvector of A
The eigenvalues as obtained above are 2 and 7.
∫
0
1
( u )−1∗1
2 x du=∫
0
1 1
u ∗1
2 x du= 1
2 x lnu
¿ 1
2 ln ( 1+12 )= π
4
ii) Binomial series
f ( x )= 1
1+ x2
The formula is stated as
( 1+x ) k=1+kx + k ( k −1 )
2 ! x2+ k ( k −1 ) ( k−2 )
3 ! x3
k =2
5. Eigenvalues and eigenvectors
A=[6 2
2 3]
Eigenvlues
Given A to be a square matrix, v a vector and λ is a scalr tht satisfy the formula Av=λv .
λ Is defines as the eigenvalue with eigenvector v of A.
hence theEigenvalues of will be obtained from the roots of the equation det ( A−λI ) =0
Hence
det ( (6 2
2 3 )−λ (1 0
0 1) ): λ2−9 λ+14
Solving for λ2−9 λ+14=0
Using the quadratic equation we obtain the values of λ as 2nd 7
This are the eigenvalues of matrix A
Eigenvectors
Being that A is a square matrix, v vector and λa scalar satisfying the eqution Av=λv ,
therefore v is an eigenvector of A
The eigenvalues as obtained above are 2 and 7.

Therefore the eigenvectors of λ=2 ;
Solving ( A−2 I ¿=[6 2
2 3 ]−2 (1 0
0 1 )= (4 2
2 1)
Solving ( 4 2
2 1 )( x
y ) =( 0
0 )
By reducing (4 2
2 1 )we obtin (1 1
2
0 0 )
Hence ( A−2 I ¿ ( x
y )= ( 1 1
2
0 0 ) ( x
y ) =( 0
0 )
This reduces to x + 1
2 y=0 , if you let y be 1 weobtain
(
−1
2
1
)
And the eigenvectors for λ=7 :
Solving ( A−2 I ¿=[6 2
2 3 ]−7 (1 0
0 1)=(−1 2
2 −4 )
(−1 2
2 −4 )( x
y )=(0
0 )
reducing (−1 2
2 −4 ) gives ( 1 −2
0 0 )
gives theSystem ( A−7 I ¿ ( x
y )= (1 −2
0 0 )( x
y )=(0
0 )
Which gives the equation x−2 y=0. isolate x=2 y nd plug ∈( x
y )
If you let y=1 , you obtain (2
1 )
Solving ( A−2 I ¿=[6 2
2 3 ]−2 (1 0
0 1 )= (4 2
2 1)
Solving ( 4 2
2 1 )( x
y ) =( 0
0 )
By reducing (4 2
2 1 )we obtin (1 1
2
0 0 )
Hence ( A−2 I ¿ ( x
y )= ( 1 1
2
0 0 ) ( x
y ) =( 0
0 )
This reduces to x + 1
2 y=0 , if you let y be 1 weobtain
(
−1
2
1
)
And the eigenvectors for λ=7 :
Solving ( A−2 I ¿=[6 2
2 3 ]−7 (1 0
0 1)=(−1 2
2 −4 )
(−1 2
2 −4 )( x
y )=(0
0 )
reducing (−1 2
2 −4 ) gives ( 1 −2
0 0 )
gives theSystem ( A−7 I ¿ ( x
y )= (1 −2
0 0 )( x
y )=(0
0 )
Which gives the equation x−2 y=0. isolate x=2 y nd plug ∈( x
y )
If you let y=1 , you obtain (2
1 )
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

The eigenvector for the matric A is thereby given by ( −1
2
1 ) ,(2
1)
6. Newton’s law of cooling
Describe Euler’s method
Application
Euler’s method is a tool that is applied in numerical arithmetic to approximate values of
solutions involving differential equations.
It applies the formula yn= yn−1 +hF ( xn−1 , yn−1 ) , where y0 isthe initial value of y and h
the step size.
Formula
yn= yn−1 +hF (xn−1 , yn −1 )
dT
dt =−1
3 T +20−10 e−t
The initial starting point is 60 with a step size of 0.5.
We therefore go from x : 0 ,0.5 , 1,1.5,2,2.5,3
Now
y1= y0 +hF(x0 , y0)
¿ 60+0.5 ( −10 )
55
y2= y1 +hF (x1 , y1 )
¿ 55+0.5∗−4.3986=52.8
y3= y2 +hF (x2 , y2 )
¿ 52.8+0.5∗(−1.2788 )=52.16
y4 = y3 +hF ( x3 , y3 )
¿ 52.16+0.5∗( 0.3820 ) =52.35
y5= y 4 +hF ( x4 , y4 )
¿ 52.35+0.5∗( 1.1966 )=52.95
2
1 ) ,(2
1)
6. Newton’s law of cooling
Describe Euler’s method
Application
Euler’s method is a tool that is applied in numerical arithmetic to approximate values of
solutions involving differential equations.
It applies the formula yn= yn−1 +hF ( xn−1 , yn−1 ) , where y0 isthe initial value of y and h
the step size.
Formula
yn= yn−1 +hF (xn−1 , yn −1 )
dT
dt =−1
3 T +20−10 e−t
The initial starting point is 60 with a step size of 0.5.
We therefore go from x : 0 ,0.5 , 1,1.5,2,2.5,3
Now
y1= y0 +hF(x0 , y0)
¿ 60+0.5 ( −10 )
55
y2= y1 +hF (x1 , y1 )
¿ 55+0.5∗−4.3986=52.8
y3= y2 +hF (x2 , y2 )
¿ 52.8+0.5∗(−1.2788 )=52.16
y4 = y3 +hF ( x3 , y3 )
¿ 52.16+0.5∗( 0.3820 ) =52.35
y5= y 4 +hF ( x4 , y4 )
¿ 52.35+0.5∗( 1.1966 )=52.95
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
y6= y5+ hF(x5 , y5)
52.95+0.5∗( 1.5292 )=53.71
y7= y6+hF(x6 , y6)
¿ 53.71+0.5∗( 1.5988 ) =54.509
Hence the value of T (3) as approximated by the Euler’s method is 53.71℃
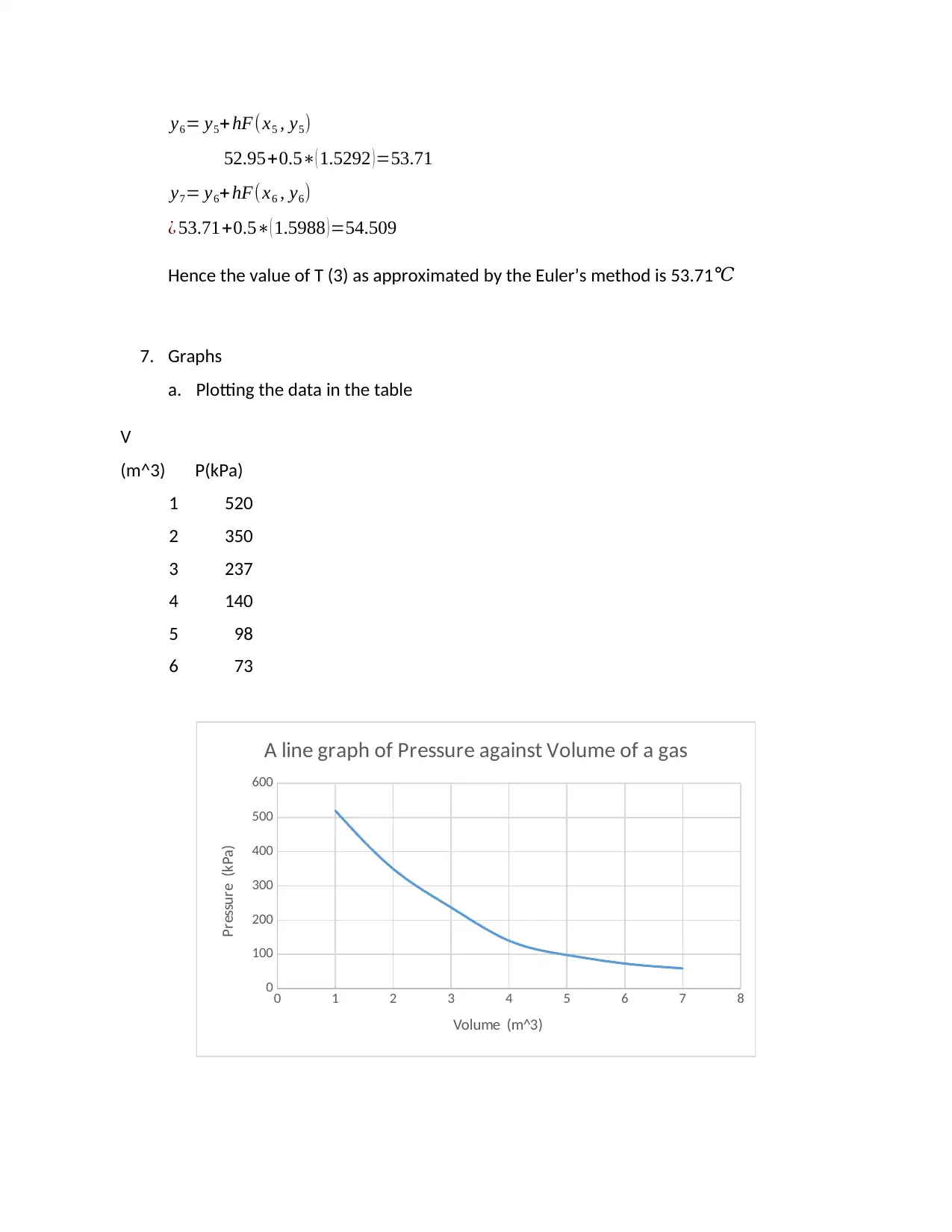
7. Graphs
a. Plotting the data in the table
V
(m^3) P(kPa)
1 520
2 350
3 237
4 140
5 98
6 73
0 1 2 3 4 5 6 7 8
0
100
200
300
400
500
600
A line graph of Pressure against Volume of a gas
Volume (m^3)
Pressure (kPa)
52.95+0.5∗( 1.5292 )=53.71
y7= y6+hF(x6 , y6)
¿ 53.71+0.5∗( 1.5988 ) =54.509
Hence the value of T (3) as approximated by the Euler’s method is 53.71℃
7. Graphs
a. Plotting the data in the table
V
(m^3) P(kPa)
1 520
2 350
3 237
4 140
5 98
6 73
0 1 2 3 4 5 6 7 8
0
100
200
300
400
500
600
A line graph of Pressure against Volume of a gas
Volume (m^3)
Pressure (kPa)

b. P=717 e−0.377 v
W is given by the formula∫
v 1
v 2
Pdv
Hence
∫
1
7
717 e−0.377 v dv
¿ 717∫
1
7
e−0.377 v dv
¿ 717 [ 1
−0.377 e−0.377 v
],¿ 1 ¿ 7
this gives 717 ¿]
¿ 717∗1.62993=1168.6598
W =1168.6598
c. Using Simpson’s rule
Formula
∫
a
b
f ( x ) dx ≈ Sn
Sn= ∆ x
3 [ f ( x0 ) +4 f ( x1 ) +2 f ( x2 ) +4 f ( x3 ) +2 f ( x4 ) +… f ( xn ) ]
∆ x= b−a
n = 7−1
6 =1
since n=6
Therefore
S6 =1
3 ¿]
¿ 1
3 [520+ 4 ( 350 ) +2 ( 237 ) +4 ( 140 ) +2 ( 98 ) +4 ( 73 ) +59]
¿ 1
3 [ 520+1400+474 +560+196+292+59 ] =1
3∗3501≈ 1167
Trapezium rule
Formula
W is given by the formula∫
v 1
v 2
Pdv
Hence
∫
1
7
717 e−0.377 v dv
¿ 717∫
1
7
e−0.377 v dv
¿ 717 [ 1
−0.377 e−0.377 v
],¿ 1 ¿ 7
this gives 717 ¿]
¿ 717∗1.62993=1168.6598
W =1168.6598
c. Using Simpson’s rule
Formula
∫
a
b
f ( x ) dx ≈ Sn
Sn= ∆ x
3 [ f ( x0 ) +4 f ( x1 ) +2 f ( x2 ) +4 f ( x3 ) +2 f ( x4 ) +… f ( xn ) ]
∆ x= b−a
n = 7−1
6 =1
since n=6
Therefore
S6 =1
3 ¿]
¿ 1
3 [520+ 4 ( 350 ) +2 ( 237 ) +4 ( 140 ) +2 ( 98 ) +4 ( 73 ) +59]
¿ 1
3 [ 520+1400+474 +560+196+292+59 ] =1
3∗3501≈ 1167
Trapezium rule
Formula
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

∫
a
b
f ( x ) dx ≈ ∆ x
2 [f ( x0 ) +2 f ( x1 ) +2 f ( x2 )+2 f ( x3 ) + 2 f ( x4 ) +… f ( xn ) ]
∆ x= 7−1
6 =1
≈ 1
2 [ 520+2 ( 350 ) + 2 ( 237 ) + 2 ( 140 ) +2 ( 98 ) +2 ( 73 ) +59 ] =1
2∗2375
≈ 1187.5
d. Comparing the results
Using integration
W =1168.6598
Using Simpson’s rule
W =1167
Using Trapezium
W =1187.5
8. Torricelli’s
a. dv
dt =−a √ 2 gh
dv
dt =−a ( 2 gh )( 1
2 )
v=∫−a ( 2 gh )
( 1
2 ) dt
v=a ( 2 gh )
( 1
2 ) t+c
v=−a ( 2∗9.8∗h )
1
2 + c
a is the cross sectional area of a circle given by π r2= 22
2 ∗( 0.025 ) 2= 11
5600
v= −11
5600 ( 98
5 h )1
2 t+ c
Hence, making h the subject t of the formula gives
a
b
f ( x ) dx ≈ ∆ x
2 [f ( x0 ) +2 f ( x1 ) +2 f ( x2 )+2 f ( x3 ) + 2 f ( x4 ) +… f ( xn ) ]
∆ x= 7−1
6 =1
≈ 1
2 [ 520+2 ( 350 ) + 2 ( 237 ) + 2 ( 140 ) +2 ( 98 ) +2 ( 73 ) +59 ] =1
2∗2375
≈ 1187.5
d. Comparing the results
Using integration
W =1168.6598
Using Simpson’s rule
W =1167
Using Trapezium
W =1187.5
8. Torricelli’s
a. dv
dt =−a √ 2 gh
dv
dt =−a ( 2 gh )( 1
2 )
v=∫−a ( 2 gh )
( 1
2 ) dt
v=a ( 2 gh )
( 1
2 ) t+c
v=−a ( 2∗9.8∗h )
1
2 + c
a is the cross sectional area of a circle given by π r2= 22
2 ∗( 0.025 ) 2= 11
5600
v= −11
5600 ( 98
5 h )1
2 t+ c
Hence, making h the subject t of the formula gives
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

h=( v
−8.6963 )
2
dh
dt = v2 d
dt (−8.6963∗10−3 t ) 2
=−1.230∗10−5 √h
b . At v¿ 0 , t=c
But at time t=0 ,the tank if full hence v=c
Since is given by π r2 h= 22
7 ∗1.52∗4=¿28.2857,
Hence the tank will be empty after 28.29 seconds.
−8.6963 )
2
dh
dt = v2 d
dt (−8.6963∗10−3 t ) 2
=−1.230∗10−5 √h
b . At v¿ 0 , t=c
But at time t=0 ,the tank if full hence v=c
Since is given by π r2 h= 22
7 ∗1.52∗4=¿28.2857,
Hence the tank will be empty after 28.29 seconds.

References
Autar, K., Egwu, K. & Duc, N., 2008. Numerical Methods with Applications. [Online]
Available at: http://nm.mathforcollege.com/topics/textbook_index.html
[Accessed 31 December 2018].
Dani, S., 2012. Ancient Indian Mathematics –. A Conspectus". Resonance. , 17(3), p. 236–246.
Autar, K., Egwu, K. & Duc, N., 2008. Numerical Methods with Applications. [Online]
Available at: http://nm.mathforcollege.com/topics/textbook_index.html
[Accessed 31 December 2018].
Dani, S., 2012. Ancient Indian Mathematics –. A Conspectus". Resonance. , 17(3), p. 236–246.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 12
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





