Engineering Mathematics: Binary Conversions and Complex Arithmetic

This mechanical engineering assignment covers a range of topics, including number conversions between binary, hexadecimal, octal, and decimal systems. It includes operations on complex numbers, such as addition, multiplication, and representation in polar and exponential forms. The assignment also explores the application of De Moivre's theorem for finding roots and proving trigonometric identities. Furthermore, it delves into AC circuit analysis, calculating impedance, and determining phase angles. The final section involves solving a system of linear equations and calculating determinants. Detailed solutions are provided for each activity, demonstrating the application of relevant formulas and theorems to solve engineering problems.

Mechanical Engineering

Table of Contents
Activity 1:........................................................................................................................................1
Activity 2.........................................................................................................................................7
Activity 3.......................................................................................................................................12
Activity 4.......................................................................................................................................15
Activity 5.......................................................................................................................................16
Activity 6.......................................................................................................................................17
Activity 7.......................................................................................................................................18

Activity 1:
a) Conversion of numbers into binary, hexadecimal, octal and decimal equivalents
(i) 10101101112
Solution:
Binary to decimal:
= 1 x 29 + 0 x 28 + 1 x 27 + 0 x 26 + 1 x 25 + 1 x 24 + 0 x 23 + 1 x 22 + 1x 21 + 1 x 20
= 512 + 0 + 128 + 0 + 32 + 16 + 0 + 4 + 2 + 1
= 69510
Binary to octal:
10101101112 = 25678
Binary to hexadecimal:
So,
10101101112 = 2B78
(ii) 53278
1

Solution:
Octal to decimal:
= 5 x 83 + 3 x 82 + 2 x 81 + 7 x 80
= 5 x 512 + 3 x 64 + 2 x 16 + 7 x 1
= 279110
Octal to binary
53278 = 1010110101112
Octal to hexadecimal
53278 = 1010110101112
0111 = 7
1101 = D
1010 = A
So, 53278 = 7DA16
(iii) 429A16
Solution: A = 10
Hexadecimal to Octal:
429A16 =
4 – 0100
2 – 0010
9 – 1001
A – 1010
So, 100001010011010
Now, regrouping them –
100 – 4
001 – 1
010 – 2
011 – 3
010 – 2
So, 429A16 = 412328
Hexadecimal to Binary:
2

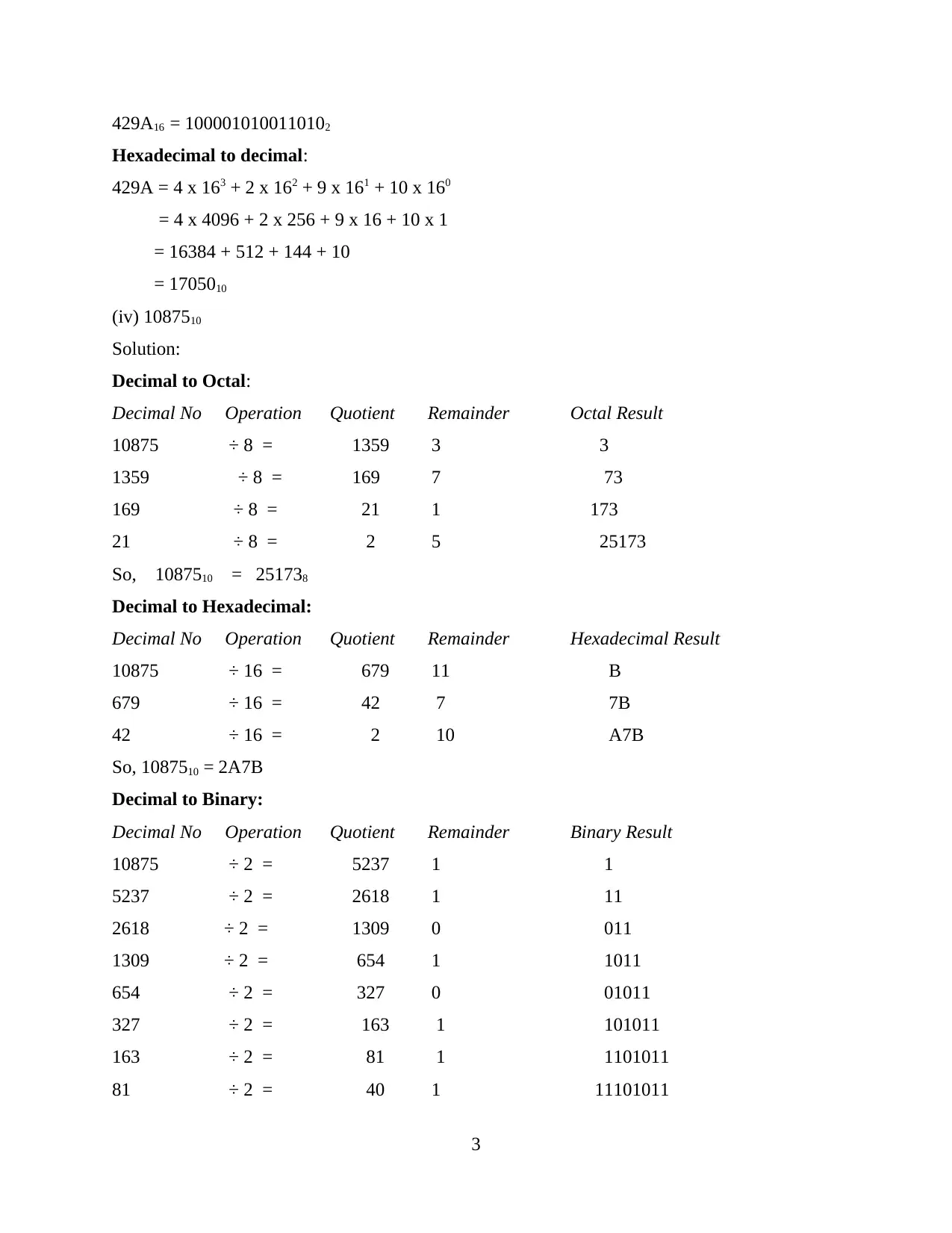
429A16 = 1000010100110102
Hexadecimal to decimal:
429A = 4 x 163 + 2 x 162 + 9 x 161 + 10 x 160
= 4 x 4096 + 2 x 256 + 9 x 16 + 10 x 1
= 16384 + 512 + 144 + 10
= 1705010
(iv) 1087510
Solution:
Decimal to Octal:
Decimal No Operation Quotient Remainder Octal Result
10875 ÷ 8 = 1359 3 3
1359 ÷ 8 = 169 7 73
169 ÷ 8 = 21 1 173
21 ÷ 8 = 2 5 25173
So, 1087510 = 251738
Decimal to Hexadecimal:
Decimal No Operation Quotient Remainder Hexadecimal Result
10875 ÷ 16 = 679 11 B
679 ÷ 16 = 42 7 7B
42 ÷ 16 = 2 10 A7B
So, 1087510 = 2A7B
Decimal to Binary:
Decimal No Operation Quotient Remainder Binary Result
10875 ÷ 2 = 5237 1 1
5237 ÷ 2 = 2618 1 11
2618 ÷ 2 = 1309 0 011
1309 ÷ 2 = 654 1 1011
654 ÷ 2 = 327 0 01011
327 ÷ 2 = 163 1 101011
163 ÷ 2 = 81 1 1101011
81 ÷ 2 = 40 1 11101011
3

40 ÷ 2 = 20 0 011101011
20 ÷ 2 = 10 0 0011101011
10 ÷ 2 = 5 0 00011101011
5 ÷ 2 = 2 1 101001111011
2 ÷ 2 = 1 0 10101001111011
So,
1087510 = 101010011110112
b) Add and multiple the following numbers
(i) 101110012 and 111010102
Solution:
Addition rules –
0 + 0 = 0
0 + 1 = 1 + 0 = 1
1 + 1 = 10
10111001
+ 11101010
110100011
Multiplication rules –
0 x 0 = 0
0 x 1 = 1 x 0 = 0
1 x 1 = 1
So, 10111001
x 11101010
1010100100011010
(ii) 21378 and 15418
Solution: Firstly, convert the numbers from octal into binary form –
21378 = 100010111112
15418 = 11011000012
Addition –
10001011111
+ 01101100001
4

11111000000
So, addition of 21378 and 15418 is 37008 (111110000002)
Similarly, multiplication of 21378 and 15418
10001011111
x 01101100001
11101100010011111111
So, multiplication of 21378 and 15418 is 35423778 (111011000100111111112)
(iii) B41E16 and 253B16
Solution:
Convert the hexadecimal numbers into binary
B41E16 = 1011010000011110
253B16 = 10010100111011
1011010000011110
+ 10010100111011
11000110101011001
So, addition of B41E16 and 253B16 is18D59
Multiplication:
1011010000011110
x 10010100111011
11010001100011101100011101010
So, multiplication of B41E16 and 253B16 is 1A31D8EA16
(iv) 356210 and 264310
Solution:
Convert decimal numbers into binary numbers as –
5

356210 = 1101111010102
264310 = 1010010100112
Addition of both numbers –
110111101010
+ 101001010011
1100000111101
So, addition of 356210 and 264310 is 620510 (11000001111012)
Now, multiplication –
110111101010
x 101001010011
100100110100100000001100
So, multiplication of 356210 and 264310 is 965223610 (11000001111012)
6

Activity 2
(a) Given,
Resistance of resistor R = 12 Ω
Inductance of coil L = 0.1 H
Capacitance C = 150 μF = 150 x 10-6 F
Amplitude of AC Voltage Source Um = 220 V
Resistor, coil and capacitor are connected in series
To determine Phase angle ø?
Current Flowing in the circuit Im ?
Figure 1: Phasor Diagram
(i) Impedance Z can be calculated by taking rectangular triangle as shown in above phasor
diagram in following way –
7

Using Pythagorean Theorem –
Z2 = R2 + (XL – XC)2
Frequency (f) = 1 / 2 √LCℼ
= 41.09
Here, XL = ωL
= 2ℼfL
= 2 x 41.09 x 0.1 = 25.80 Ωℼ
and XC = 1/ ωC
= 1/ 2ℼfC
= 1/ 2ℼ x 41.09 x 150 x 10-6
= 25.84 Ω
So, Impedance in rectangular form –
Z = R + j (XL – XC)
= 12 + j (25.80 – 25.84)
= 12 – j 0.4 Ω
Impedance in polar form –
Z = 12.01 (-1.91 ) Ω⁰
(ii) Impedance at resonance,
At resonance XL = XC
Therefore,
Impedance at resonance in rectangular form
Z = R + j. 0
= 12 Ω
Impedance at resonance in polar form
Z = 12 (0 ) Ω⁰
(iii) Current Flowing in rectangular form –
I = V / Z
= 220 / 12 – j 0.4
In polar form –
8

I = V / Z
= 220 / 12.01 (-1.91 )⁰
(b) Given,
Resistance of resistor R1 = 1k Ω, R2 = 3k Ω, R3 = 5k Ω,
Inductance of coil L = 100 mH = 10 x 10-3 H
Capacitance C = 50 μF = 50 x 10-6 F
Amplitude of AC Voltage Source Um = 240 V
Resistor, coil and capacitor are connected in series
To determine Total Impedance (Z)?
Admittance (Y)
Current Flowing in the circuit Im ? Phase relative to applied voltage ?
Firstly,
As series is connected in parallel, therefore,
1 = 1 + 1 + 1
R R1 R2 R3
= 1 + 1 + 1
1 3 5
= 23/ 15
Or, R = 15/23 = 0.652k Ω = 652 Ω
Frequency (f) = 1 / (2 √LC)ℼ
= 71.18
XL = ωL
= 2ℼfL
= 2 x 71.18 xℼ 100 x 10-3 = 44.70 Ω
and XC = 1/ ωC
= 1/ 2ℼfC
= 1/ 2ℼ x 71.18 x 50 x 10-6
= 44.74 Ω
So, Impedance in the circuit can be calculated by –
Z = 1 .
9