Mechanical Engineering Assignment: Solutions to Various Problems

This mechanical engineering assignment presents solutions to a variety of problems covering different concepts in the field. The assignment begins with a problem on viscous dampers, calculating the piston diameter given damping constants and fluid properties. It then moves on to a model simulating a human head's response to a frontal blow, determining maximum acceleration and spring deflection. The assignment also includes a problem on determining the moment of inertia of aircraft propellers using bifilar suspension, and analyzes the behavior of a steel ball falling onto a spring-supported tabletop, deriving velocity expressions and discussing energy dissipation. Furthermore, the assignment presents problems related to a hoisting system and a railway buffer, analyzing the motion of a basket and the train's behavior during a collision, respectively. Finally, the assignment concludes with a problem on a door closing mechanism controlled by a spring and dashpot, deriving an expression for the door's motion and estimating the closing time. Each problem includes detailed step-by-step solutions, calculations, and explanations, making it a valuable resource for students studying mechanical engineering.

Unit name:
Title of experiment:
Date:
Student ID:
Student name:

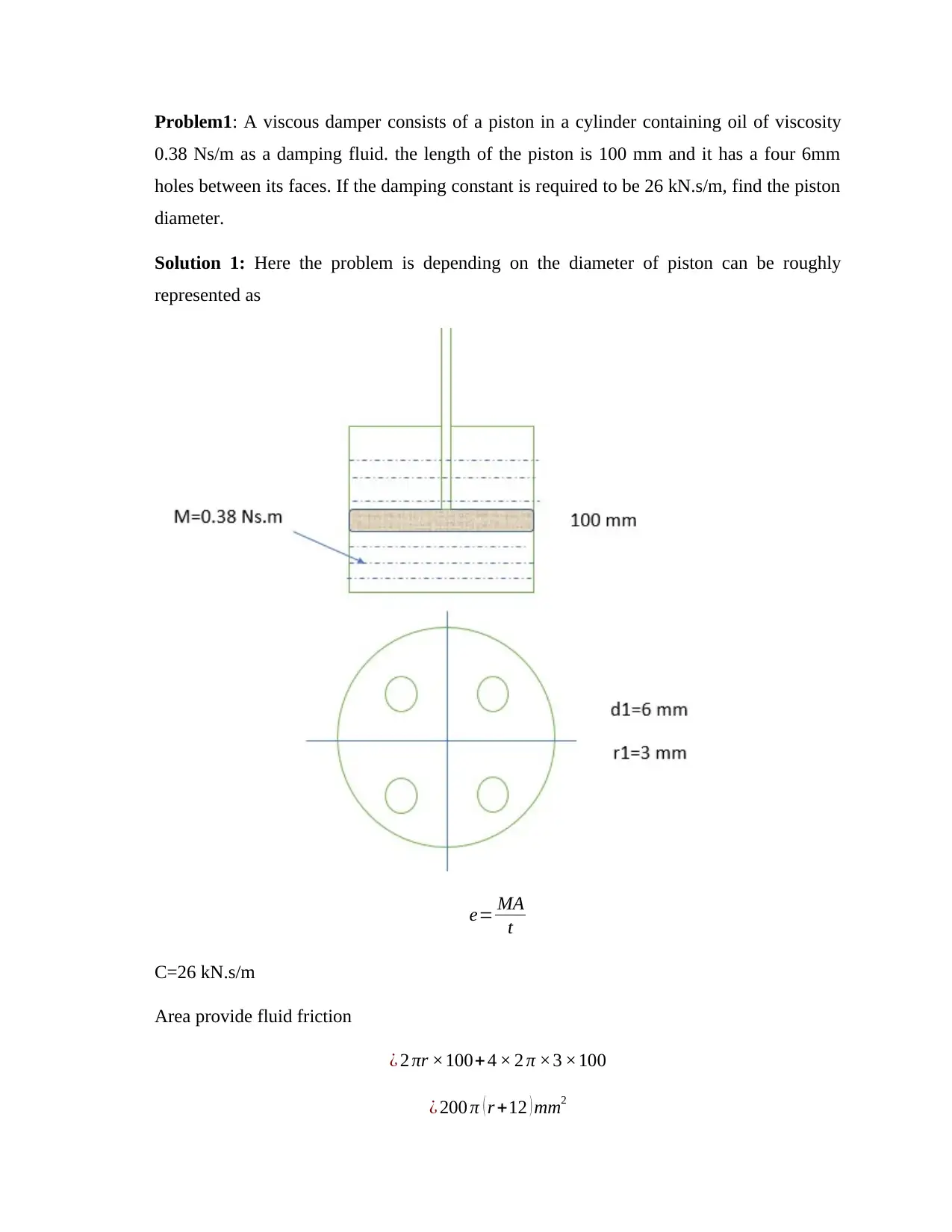
Problem1: A viscous damper consists of a piston in a cylinder containing oil of viscosity
0.38 Ns/m as a damping fluid. the length of the piston is 100 mm and it has a four 6mm
holes between its faces. If the damping constant is required to be 26 kN.s/m, find the piston
diameter.
Solution 1: Here the problem is depending on the diameter of piston can be roughly
represented as
e= MA
t
C=26 kN.s/m
Area provide fluid friction
¿ 2 πr ×100+ 4 × 2 π ×3 ×100
¿ 200 π ( r +12 ) mm2

Here t=3 mm
So,
26 ×1000= 0.38(200 π ( r +12 ) )
3× 1000
200 π ( r + 12 )=78000000
0.38
( r +12 ) =326686.46
r =326674.46 m
Diameter of piston is 6.5 x 105 m
Problem 2: A model was designed to simulate the response of a human head to a frontal
blow. the model has a mass of 4.7 kg horizontally supported by a spring of stiffness 2000
N/m. If a blow of 400 N was applied to the mass over a period of 0.003 seconds. Find the
maximum acceleration which the mass is subjected to as a result of this blow. What’s the
maximum deflection in the spring.
Solution 2:
We know
F.t= change in momentum
Ft=mV f −mV i

Since V i=0
V f =Ft
400 × 0.003=4.7 V f
V f =0.255 m/second
Total work done
¿ ∆ K . E ( kinetic energy )
1
2 K x2= 1
2 mV f
2
2000 x2=4.7 ( 0.255 ) 2
x=12.377 mm
We knowcF=ma
400=4.7 amax
amax=85.106 m/s2
Problem 3: Determine the moment of inertia of a two-blade aircraft propeller about its
rotational axis from the observation of natural frequency of the free oscillation of the
propeller when suspended from two light wires attached to the tips of the blades. The
length of each wire is h, the diameter of the propeller is D, and its weight is W. Repeat the
problem for the case of three blade propellers suspended by three wires. Does the result
depend on the number of wires?
Solution 3:

Two blade aircraft propeller can be considered as bifilar suspension system where the
tension in wire A and B can be written as
T A=T B =T = W
2
And the resisting torque due to small displacement is given as
T =T A ×∅ × r1 +T B ×∅ × r1
Torque
T =2 T ∅ r1=W ×∅ ×r
For geometry
∅ = rθ
l
By solving above equations, we can get
T = W r2 θ
l
We know torque is given as
T =Iα

And
I = W k2
g
α= T
I =
W r2 θ
l
W k2
g
And we also know that
W 2= Angular acceleration
Angular displacement = α
θ
By solving equation we will get
K2= g r2
lW 2
By susbstituting the value of K2 in the equation of I
I =
W g r2
lW 2
g
I = W r2
lW 2
Form last equation we can determine the mass moment of inertia of blade of aircraft
propeller.
Similarly, the three-blade aircraft propeller can be considered as trifiller suspension
Then tension in each wire=W/3
If it is displaced by some small angle θ then
Accelerating torque= restoring torque.

I = W k2
g α= ( W
3 ∅ × r ) × 3
Where ∅ = r θ
l
W k2
g α = W r2 θ
l
α = r2 θ
l K2 g
But
W 2= Angular acceleration
Angular displacement = α
θ
W2= g r2
lK2
K2= g r2
lW 2
But
I = W
g K2= W r2
lW 2
I = W r2
lW 2
Which is similar in both case hence moment of inertia does not depends on number of
wires.
Problem 4: A steel ball of mass m (kg) is held at a distance h (m) above the massless rigid
tabletop supported by undamped spring whose equivalent stiffness is k (N/m). If the ball is
left to fall from rest on the tabletop. Deduce an expression for the velocity at which the ball

will bounce back to the tabletop. On its way back will the mass bounce back to its initial
height? If it will not where will the difference in energy go? Discuss mathematically!
Solution 4:
Let’s start from the moment ball is released
1. When the ball falls with some velocity the ball keeps hitting number of molecules
of air and the air molecules obstruct the ball. This obstructing force is drag (D)
D= 1
2 ρ V 2 CD A
Where ρ=density of air
v−velocity of ball
A=area of ball=π r2
CD −drag coefficient
And while falling ball does work on air by pushing and displacing the air molecules
thereby giving kinetic energy to air molecules
W =work done=∫
H
0
D .ds
Energy left with ball just before hitting
Table= E=1
2 Mball V 1
2
Where V 1=velocity of ball just before hitting table
E can also be written as
E=M ball . g . H−W
E=M ball . g . H−W −∫
H
0
1
2 ρV 2 CD A . ds
Here V is dependent on ds which makes the integration complicated

Lets see how to find expression of V
We know F=ma
F=ma=m ¨x=m ˙v
mg− 1
2 ρ V 2 A C D=m ¨x=m dV
dt
dV
m = dV
mg− 1
2 ρ V 2 A CD
We can find expression of V by integrating
So lets write
E=Mball . g . H−W −∫
H
0
1
2 ρV 2 CD A . ds
E=1
2 Mball V 1
2
V 1−velocity of ball before hittingtable
V 1= √ 2 E
Mball
=¿ √ 2 gH−∫
H
0 ρ V 2 CD A . ds
M ball
¿
Since undamped springs only store energy and release, springs consume no energy and
assuming that throughout the recoil of spring ball is in contact with spring: ball rebounces
with some speed V 1
And ball doesn’t rise to the initial height (H) because energy of ball has been decreased by
W and the ball will also further dissipate energy in its rise. The dissipated energy will
excite air molecules and temperature rises.
Problem 5: A hoisting system consist of a light of 3m bar hanging vertically of a small
servo driven trolley. The bar is allowed to swing on its hinge which is controlled by spring
of stiffness 10 kNm/rad and a damper whose damping coefficient is 800 Nms/rad. The
trolley travels on track build 4m about the floor level at the speed profile shown in the

figure. The total mass of the basket and the slewing mechanism is equivalent to 70 kg
acting at the lower end of the bar. The system is designed to handle a payload of 800 kg.
Plot the motion of the basket against the time as the trolley travels between the two loading
stations. how far should the operator keep clear from the loading and unloading stations
when the system is in operation?
Problem 6: A railway buffer consist of a pair of cylinders placed parallel side by side. oil
is present in each cylinder and is arranged to bypass through ports thereby producing a
damping resistance which is proportional to the velocity of the piston within the cylinder.
the magnitude of this resistance is 50 kN at a velocity of 0.25 m/s. Each cylinder also
contains a compression spring, initially with negligible compression of stiffness 65kN/m. A
rigid train of mass 250 tons is moving at a speed of 1.6m/s and collides with the buffer.
determine the distance taken by train before first coming to rest. Assuming that the train
comes into contact and then become attached to the free end of the buffer. Determine the
time it takes the train to come to complete stop. solution for this problem should show the
position and velocity of train.
Solution 6:
Pictorial representation of the problem situation as seen rom top.

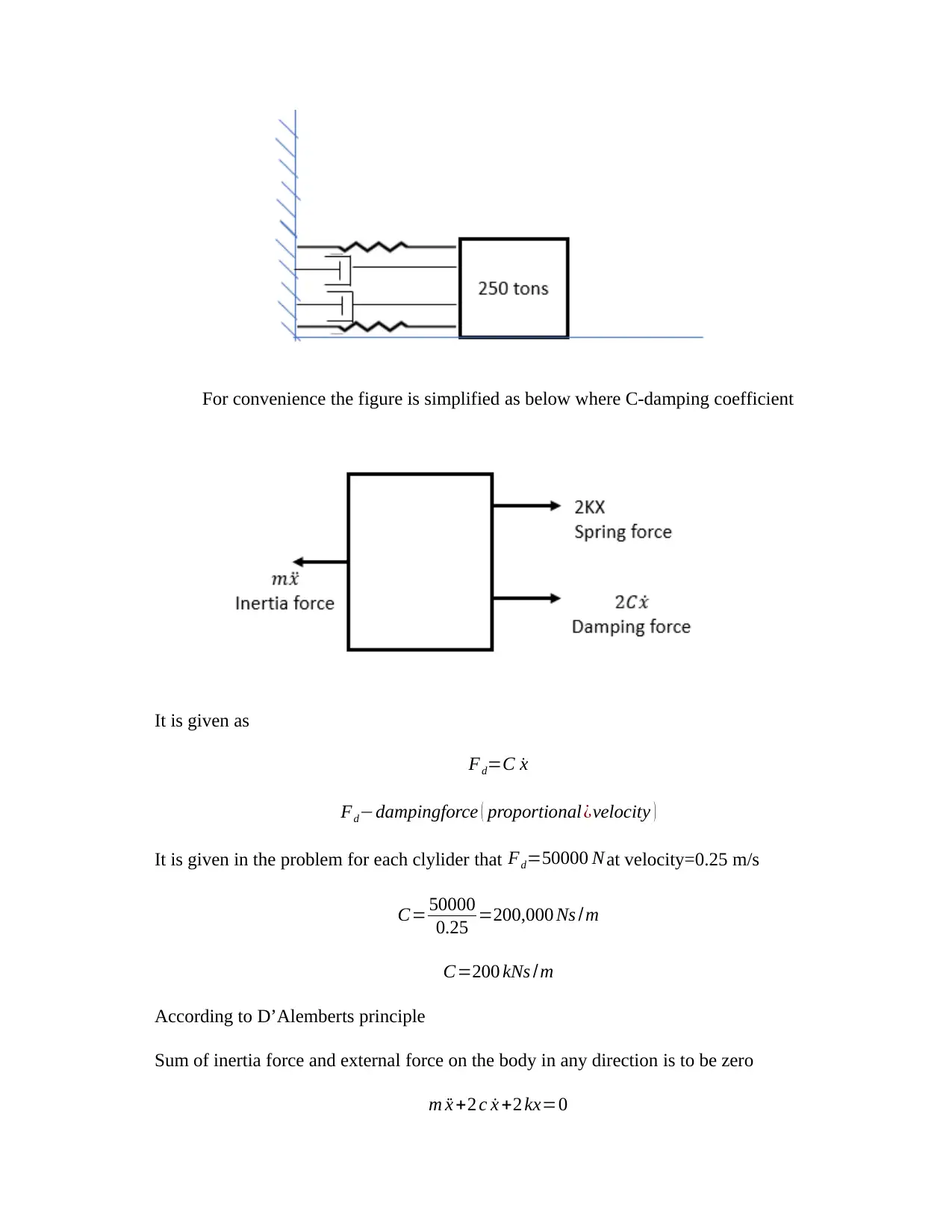
For convenience the figure is simplified as below where C-damping coefficient
It is given as
Fd=C ˙x
Fd−dampingforce ( proportional¿velocity )
It is given in the problem for each clylider that Fd=50000 N at velocity=0.25 m/s
C= 50000
0.25 =200,000 Ns / m
C=200 kNs /m
According to D’Alemberts principle
Sum of inertia force and external force on the body in any direction is to be zero
m ¨x +2 c ˙x +2 kx=0

¨x +2 c
m ˙x +2 k
m x=0
The solution of the above differential equation is of the form
x= A eα1 t +B eα2 t
α1 andα 2 are roots of auxiliary equation given as
α2+ 2 c
m α + 2k
m =0
The roots of equation given as
α 1,2=−c
m ± √ (2 c
m )2
−4 (2 k
m )
2
α 1,2=−c
m ± √ ( c
m )2
− (2 k
m )
The ratio ( c
m )2
¿ ( 2k
m )is called the damping factor denoted by ε
ε =
√ ( c
m )
2
( 2 k
m ) = c
mwn
wn natual frequency
ε = 200,000
250 x 1000 √ 2× 65000
250 ×1000
ε=1.109 overdamped system
After substituting ε = c
mwn
it can be re write as

α 1,2=−ε wn ± √ ( ε wn )
2 −wn
2
α 1,2=wn ¿
Substituting alpha value in the differential equation
wn= √ 2× 65000
250× 1000
wn=0.72 rad /s
x= A e−0.63 t + B e−1.58 t
Differentiating with respect to t
˙x=(−0.63) A e−0.63 t +(−1.58)B e−1.58 t
It has been given that ˙x=1.6 m
s when t=0
1.6=−0.63 A−1.58 B
Also t=0, x=0 substitute in equation
0=A+B i.e A=-B
So overall solution B= -.1684 and A= 1.684
After substituting the value of A and B in equation finally we get the value of xdot
˙x=−1.060 e−0.63 t +2.66 e−1.58 t
To find the distance of train travels before coming to rest we need time t at which ˙x=0 and
then we would susbstitute this t in the equation of x.
Putting ˙x=0
t=0.968 second
Substituting this value in other equation of x
x=0.549 m
The train covers a distance of x=0.559 m before coming to complete stop

It take 0.968 seconds to come to complete stop.
Problem 7: A door is closed under the control of spring and a dashpot. the spring produces
a torque of 12.5 Nm when the door is closed and has a stiffness of 50 Nm/rad. the dashpot
has a damping constant of 100 Nms/rad and moment of inertial of the door about its hinges
is 90 kg m2. derive an expressing for a motion of the door if it was opened 110degree and
released. find the approximate time it takes to close.
Solution 7:
Initial spring torque =12.5 N.m
So torque due to spring when door open at θ
Spring torque=50xθ-12.5
Now torque due to dashpot
Dashpot torque= - 100 x w (negative because applied in opposite direction)
So final torque=50 x θ-12.5-100xw
We know torque= αI =90 xd
Here given that θ=110=100 π
180 rad
θ=1.92rad
So after solving equation we get
90 × d=50 ×1.92−12.5−100 ×w
90 × d=83.5−100× w
We know that
w=w0 +dt
But we know w0=0
Initial speed is zero when it start to close

w=α ( t )
90 × w
t =83.5−100 × w
w (90 × 100
t )=83.5
w= 83.5 t
(90t +100)
Above expression of motion
And we know that
θ=w0 t +1
2 t2
As we derive w=dt and w0=0
θ=1
2
w
t t2
θ=1
2
83.5 t2
(90 t+100) =1.92
345.6 t+ 384=83,5t2
t=5.0496 second
References:
1. Hubbard, M., 2000. The flight of sports projectiles. Biomechanics in sport, pp.381-400.
2. Gress, G.R., 2004. VTOL aircraft control using opposed tilting of its dual propellers or fans.
U.S. Patent 6,719,244.