Mechanical Engineering: Engineering Mathematics 1 Assignment Solution

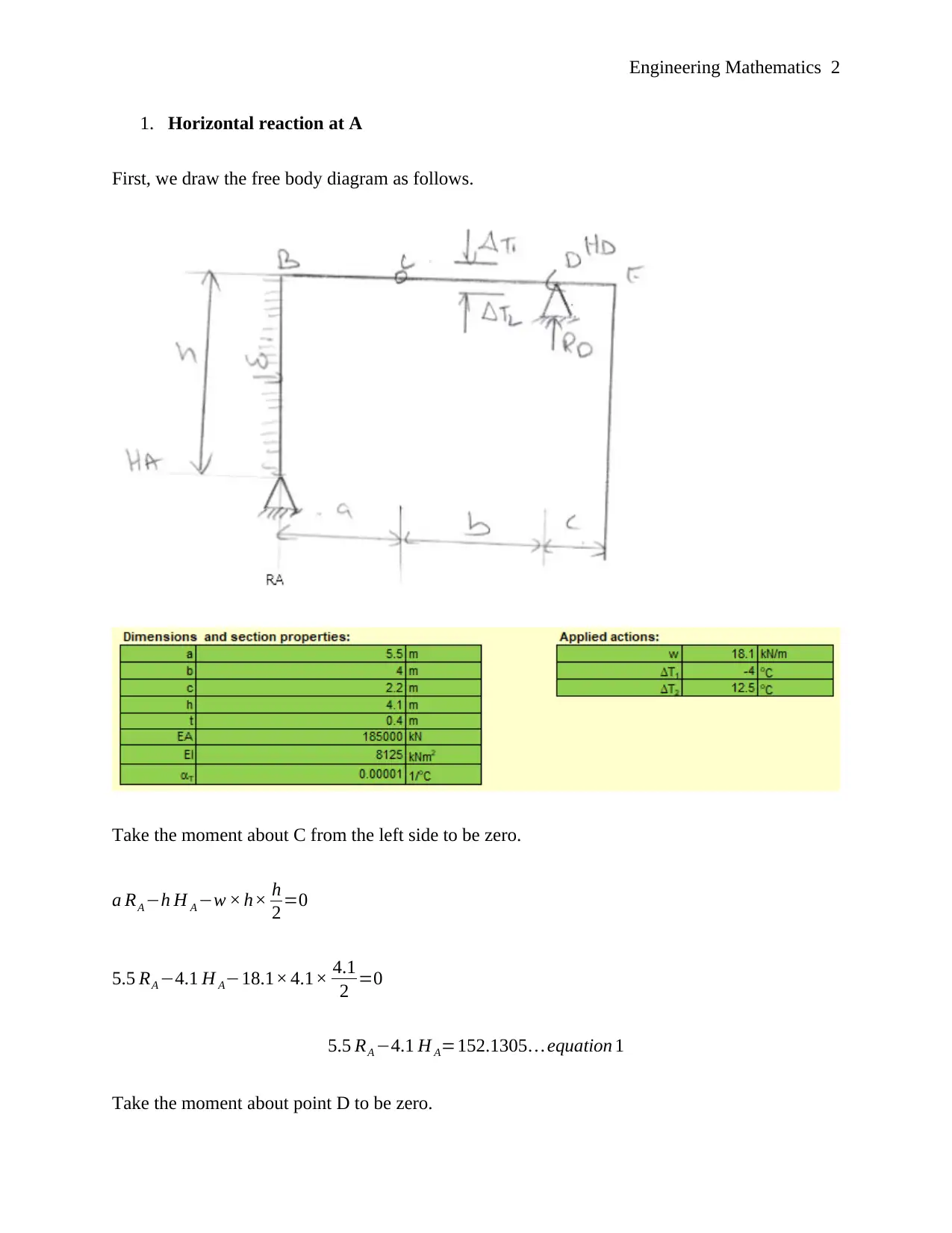
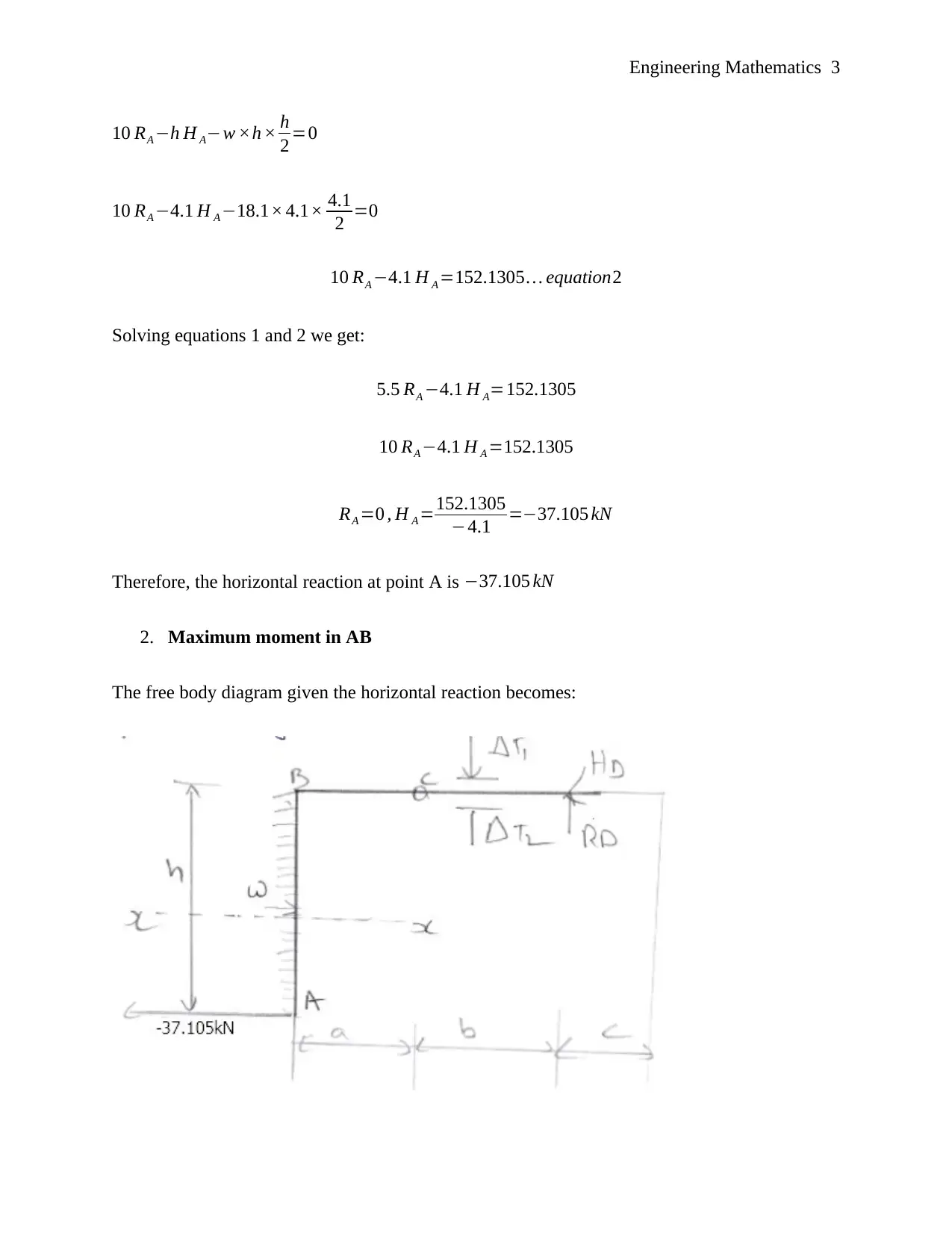
This document presents a comprehensive solution to an Engineering Mathematics assignment, covering various aspects of structural analysis and mechanics. The solution begins by calculating the horizontal reaction at a specific point using moment equilibrium equations. It then determines the maximum moment in a structural member. The assignment further explores the uniform strain component and curvature in a member, followed by calculating the vertical displacement and relative rotation at specific points. The solution then analyzes a scenario with a distributed load, determining reactions, maximum moment, and strain energy. It also considers the effects of initial curvature and support settlement on the horizontal displacement. The final section combines these elements to calculate the overall horizontal displacement at a point. The solution includes free body diagrams and detailed calculations, making it a valuable resource for students studying engineering mathematics and structural analysis. This assignment is contributed by a student and available on Desklib.

Engineering Mathematics 1
Engineering Mathematics
Student’s Name
Course
Professor’s Name
University
City (State)
Date

Engineering Mathematics 2
1. Horizontal reaction at A
First, we draw the free body diagram as follows.
Take the moment about C from the left side to be zero.
a RA −h H A −w × h× h
2 =0
5.5 RA −4.1 H A−18.1× 4.1× 4.1
2 =0
5.5 RA −4.1 H A=152.1305… equation 1
Take the moment about point D to be zero.

Engineering Mathematics 3
10 RA −h H A−w ×h × h
2 =0
10 RA −4.1 H A −18.1× 4.1× 4.1
2 =0
10 RA −4.1 H A =152.1305… equation2
Solving equations 1 and 2 we get:
5.5 RA −4.1 H A=152.1305
10 RA −4.1 H A =152.1305
RA =0 , H A =152.1305
−4.1 =−37.105 kN
Therefore, the horizontal reaction at point A is −37.105 kN
2. Maximum moment in AB
The free body diagram given the horizontal reaction becomes:

Engineering Mathematics 4
M xx =37.105 x − w x2
2 =37.105 x−9.05 x2
Differentiating the equation with respect to x yields:
d M xx
dx =37.105−18.1 x
For maximum moment, d M xx
dx =0
d M xx
dx =37.105−18.1 x=0
18.1 x=37.105
x= 37.105
18.1 =2.05 m
Maximum moment∈ AB, Mxx =37.105 ( 2.05 )−9.05 ( 2.05 )2=38.03262 5 kNm
3. Uniform strain component ε T in member BCD
Uniform strain component , δT =α T ∆ T =α T ( ∆ T 2−∆T 1 )
¿ 0.00001 ( 12−−4 )=1.6× 10−4
Hence , theuniform strain component , δ T=1.6× 10−4
4. Curvature ϕT in member BCD
ϕT = 1
lBCD α T ∆ T = 1
( a+b ) δT
¿ 1
( 5.5+ 4 ) 1.6 × 10−4

Engineering Mathematics 5
¿ 657.8947
5. Vertical displacement ∆E at point E
The vertical displacement is zero
6. Relative rotation rel φC at point E
Since point C is pin connected, rel φC= δ
c = 0
2.2 =0
Section 2
1. Case 1: Distributed load acting on member BC only
The free body diagram of member BC is shown below.

Engineering Mathematics 6
RB=RC = wb
2 = 11.5 ×5.7
2 =32.775 kN
The maximum moment in member BC is m= w b2
8 = 11.5 ×5.72
8 =46.704375 kNm
Strain energy stored in member BC is U = m2 b
2 EI = 46.7043752 ×5.7
2× 20625 =0.301416 kNm
From Castigliano’s theorem, δc= U
RC
=0.301416
32.775 =9.19652× 10−3 m
The horizontal displacement, δ c=9.19652 ×10−3 m
2. Case 2: Initial curvature in member AB only
¿ the given figure , tan θ= h
a , θ=tan−1
( h
a )=ta n−1
( 4.5
3 )=56.3099 °
The curvature ϕ AB=ϕ0 × I AB =ϕ0 × a
cos θ
¿ 4 ×10−4 × 3
cos 56.3099° =2.1633 ×10−3 rad m−1
The horizontal displacement due to curvature in member AB, δc H =ϕAB × sinθ
¿ 2.1633 ×10−3 ×sin 56.3099 °

Engineering Mathematics 7
δ c H =1.8 ×10−3 m
Case 3: Support settlement at point D
Support settlement , ∆ CδD=δD × b
h =0.019× 5.7
4.5 =24 . 067 ×10−3 m
Case 4
The free body diagram to calculate the support reactions is shown below.
The horizontal reactions at the supports will cancel out each other.
Now, considering the vertical forces,
A y+ D y=wb=11.5 × 5.7=65.55 kN
Considering the moment equilibrium at point D.
A y ( a+ b )− w b2
2 =0

Engineering Mathematics 8
A y ( 3+5.7 ) −11.5 ×5.72
2 =0
A y=11.5 ×5.72
2 × 1
(3+5.7) =21.4733 kN
But A y+D y=65.55 kN
so that , D y=65.55 kN− A y=65.55 kN −21.4733 kN =44.0767 kN
From the free body diagram above, F AB= A y
sinθ = 21.4733 kN
sin 56.3099 =25.8077 kN
Therefore, the force in member AB, F AB=25.8077 kN
Horizontal displacement at point C=δc−δc H +∆ CδD
¿ ( 9.19652−1.8+24.067 ) ×10−3 =31.46352×10−3
Therefore , theh orizontaldisplacement at point C=0.03146352 m