Analysis of I-Section and Beam: Mechanical Engineering Project

This project presents a detailed structural analysis, commencing with the determination of the centroid and the second moment of area for an I-section. It involves breaking down the I-section into segments to calculate the centroid's position and then using the parallel axis theorem to find the second moment of inertia. The project then proceeds to analyze a beam with distributed and point loads, determining reactions and moments at fixed ends. It involves converting the distributed load into a point load, calculating support reactions, and deriving the bending moment equation. The project further includes the calculation of slope and deflection at various points along the beam, utilizing integration and boundary conditions to solve for these parameters. Finally, the project determines the maximum deflection of the beam and deflection curves.

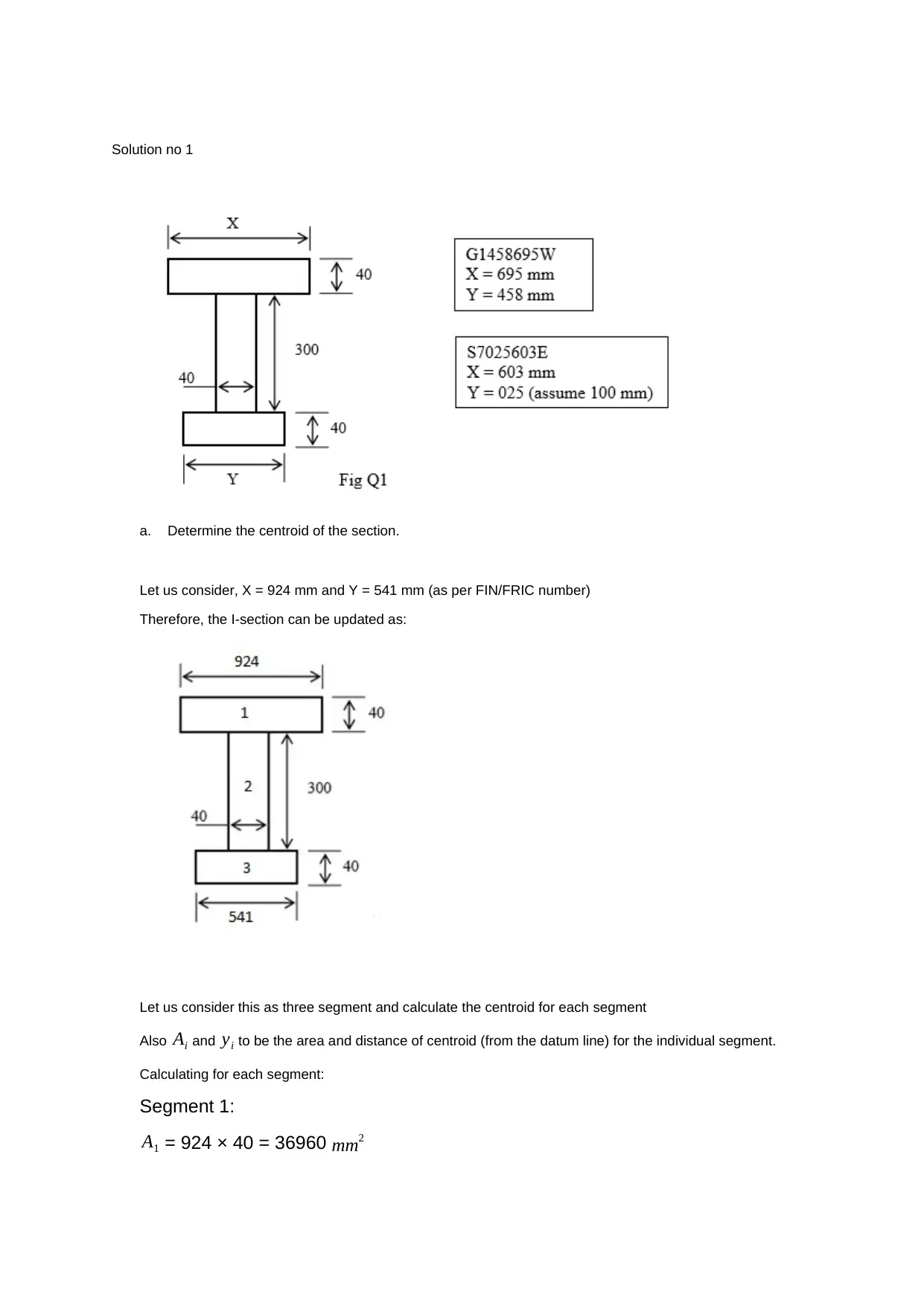
Solution no 1
a. Determine the centroid of the section.
Let us consider, X = 924 mm and Y = 541 mm (as per FIN/FRIC number)
Therefore, the I-section can be updated as:
Let us consider this as three segment and calculate the centroid for each segment
Also Ai and yi to be the area and distance of centroid (from the datum line) for the individual segment.
Calculating for each segment:
Segment 1:
A1 = 924 × 40 = 36960 mm2

y1 = 40 + 300 + 40
2 = 360 mm
Segment 2:
A2 = 40 × 300 = 12000 mm2
y2 = 40 + 300
2 = 190 mm
Segment 3:
A3 = 541 × 40 = 21640 mm2
y3 = 40
2 = 20 mm
Now,
Ӯ (Centroid of the I-section) = ∑ Ai yi
∑ Ai
= A1 y1 + A2 y2+ A3 y3
A1+ A2+ A3
=
( 36960× 360 ) +(12000 ×190)+(21640× 20)
36960+12000+21640
= 13305600+2280000+ 432800
70600 = 16018400
70600 = 226.89 mm
b. Determine the second moment of area about a horizontal axis at the centroid of the section.
To calculate the second moment of inertia, we need to use the “Parallel Axis
Theorem”:
I total = ∑ (I i¿+ Ai di
2 )¿
Where,
di = Vertical distance from the centroid of the segment to the neutral axis
Ai = Area of the segment
I i = Moment of Inertia of the section
We also know that, for rectangular Section:
I = 1
12bh3
b = width of rectangle
h = height of rectangle

Now, consider the individual segment:
Segment 1:
I 1 = 1
12 ¿924 * 403 ¿ = 5913600/12 = 492800 mm4
A1 = 924 × 40 = 36960 mm2
d1 = ( y1 - ẏ) = 360 – 226.89 = 133.11 mm
Segment 2:
I 2 = 1
12 (40 * 3003) = 1080000000/12 = 90000000 mm4
A2 = 40 × 300 = 12000 mm2
d2 = ( y2 - ẏ) = 190 – 226.89 = 36.89 mm
Segment 3:
I 3 = 1
12 (541 * 403) = 34624000/12 = 2885333 mm4
A3 = 541 × 40 = 21640 mm2
d3 = ( y3 - ẏ) = 20 – 226.89 = 206.89 mm
I total = ∑ (I i¿+ Ai di
2 )¿
I total = ( I ¿¿ 1+ A1 d1
2 )¿ + (I ¿¿ 2+ A2 d2
2 )¿ + (I ¿¿ 3+A3 d3
2)¿
I total = ( 492800+ ( 36960∗133.112 ) ) + (90000000+ ( 12000∗36.892 ) ) + ¿
I total =655360136+ 1508346720 + 929152469.244
I total = 3092859325.244 mm4 = 3.09 * 109 mm4
Solution no 2
Now, according to the Id, W = 24 KN/m and Y = 19 KN

Incorporating the values, we have
a. Determine the reactions and moments at the fixed ends
The free body diagram can be represented as:
For further calculation, the distributed load is to converted into point load.
The distributed load: 24 KN/m
Or, it can be represented as: 24 * 4 = 96 KN point load (at the distance of 2m
from A)
Now, equating the forces vertically,
RA + RB = 96 + 19 = 115 KN (equation 1)
Now, Consider the moment at fixed point A
∑ (M A ¿) ¿ = 0
Or, (96 *2) + (19*6) – ( RB * 8) = 0
Or, 8 RB = 192+114
Or, RB = 306/8 = 38.25 KN
Hence, from Equation 1

RA = 115 – 38.25 = 76.75 KN
Considering B as origin
Equation of Bending Moment, M = M B + ( RB∗x) – 19 ( x – 2) - 24
4 (x−4)2
Or, EI d2 y
dx2 = M B + ( RB∗x) – 19 ( x – 2) - 6( x−4)2
Integrating the above equation, we get
EI dy
dx = M B x + ( RB∗x2
2 ) – 19
2 ( x−2)2 - 2(x−4)3 + C1
At end B, x= 0, slope dy
dx = 0, because of fixed end
So,
0 = 0 + 0 – omitted term + C1
Or, C1 = 0
Hence, the equation can be written as:
EI dy
dx = M B x + ( RB∗x2
2 ) – 9.5 ( x−2)2 - 2( x−4)3
Integrating this equation, we get
EIy = MB
x2
2 + ( RB∗x3
6 ) – 9.5
3 (x−2)3 - 0.5( x −4)4 + C2
At end B, x= 0, slope dy
dx = 0, because of fixed end
So,
0 = 0 + 0 – omitted term + C2
Or, C2 = 0

Finally, the equation becomes:
EIy = MB
x2
2 + ( RB∗x3
6 ) – 9.5
3 (x−2)3 – 0.5 (x−4)4
To determine the moment, let us consider end A where x = 8 m and both
slope and deflection are zero
Putting the values in the equation:
EIy = M B
x2
2 + ( RB∗x3
6 ) – 9.5
3 (x−2)3 - (x−4)4
0 = M B
82
2 + ( RB∗83
6 ) – 9.5
3 (8−2)3 – 0.5(8−4 )4
0 = 32 MB+ 85.33 RB–684 – 128
We know that, RB = 38.25 kN
Hence, the equation becomes:
0 = 32 MB+ (85.33* 38.25)–684 – 128
32 M B = 2451.875
M B =−¿2451.875/32 = -76.6 KN/m
Slope at 7 m
Putting x = 7 m in equation EI dy
dx = M B x + ( RB∗x2
2 ) – 9.5 (x−2)2 - 2( x−4)3
EI dy
dx = M B x + ( RB∗x2
2 ) – 9.5 ( x−2)2 - 2( x−4)3
Considering E = 210 * 104 MPa = 210 * 107 KN/m2
And, I = 3.09 * 109 mm4
(210 * 107 * 0.00309¿ dy
dx = M B x + ( RB∗x2
2 ) – 9.5 (x−2)2 - 2( x−4)3
(210 * 107 * 0.00309¿ dy
dx = −76.6∗7 + ( 38.25∗72
2 ) – 9.5 (7−2)2 - 2(7−4 )3

(210 * 107 * 0.00309¿ dy
dx = −536.2+ 937.125 – 237.5 - 54
(210 * 107 * 0.00309¿ dy
dx = 109.425
dy
dx = 109.425/(210 * 107 * 0.00309¿ = 0.0000168632
Deflection at x = 7
EIy = MB
x2
2 + ( RB∗x3
6 ) – 9.5
3 (x−2)3 - (x−4)4
6489000y = -1879.5 + 2186.625 – 395.8 - Omitted term
y = -89.3/6489000 = -0.000013 m = -0.013 mm
Max Deflection will be at x = 3.198
EIy = MB
x2
2 + ( RB∗x3
6 ) – 9.5
3 (x−2)3 - (x−4)4
6489000y = M B
3.1982
2 + ( RB∗3.1983
6 ) – 9.5
3 (3.18−2)3 - (x−4)4
6489000y = −396.8 + 6819 – 7.804 -Omitted term
y = 0.00988 = -9.8 mm
Deflection Curve