Mechanical Engineering Thermodynamics Quiz Solution - University Name

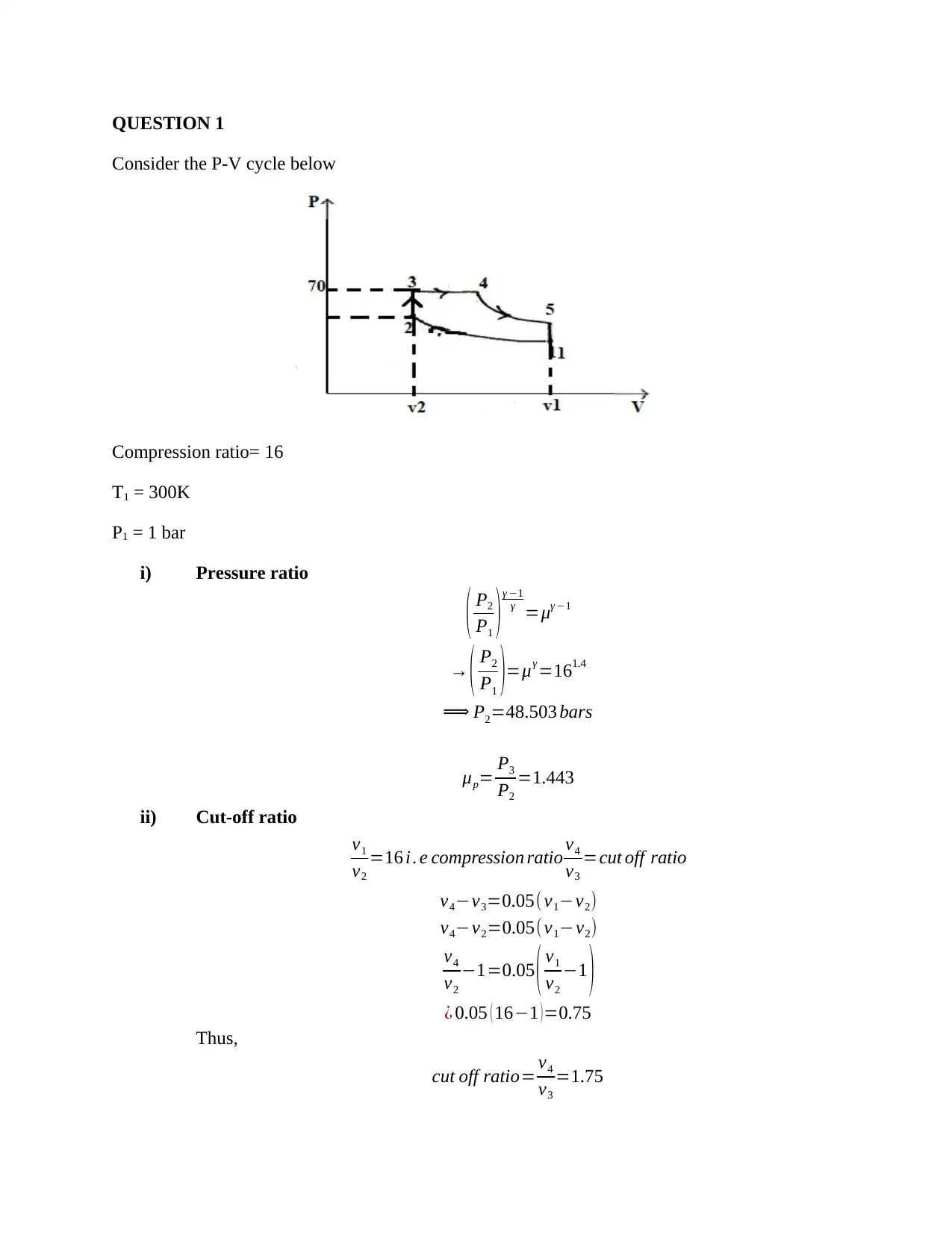
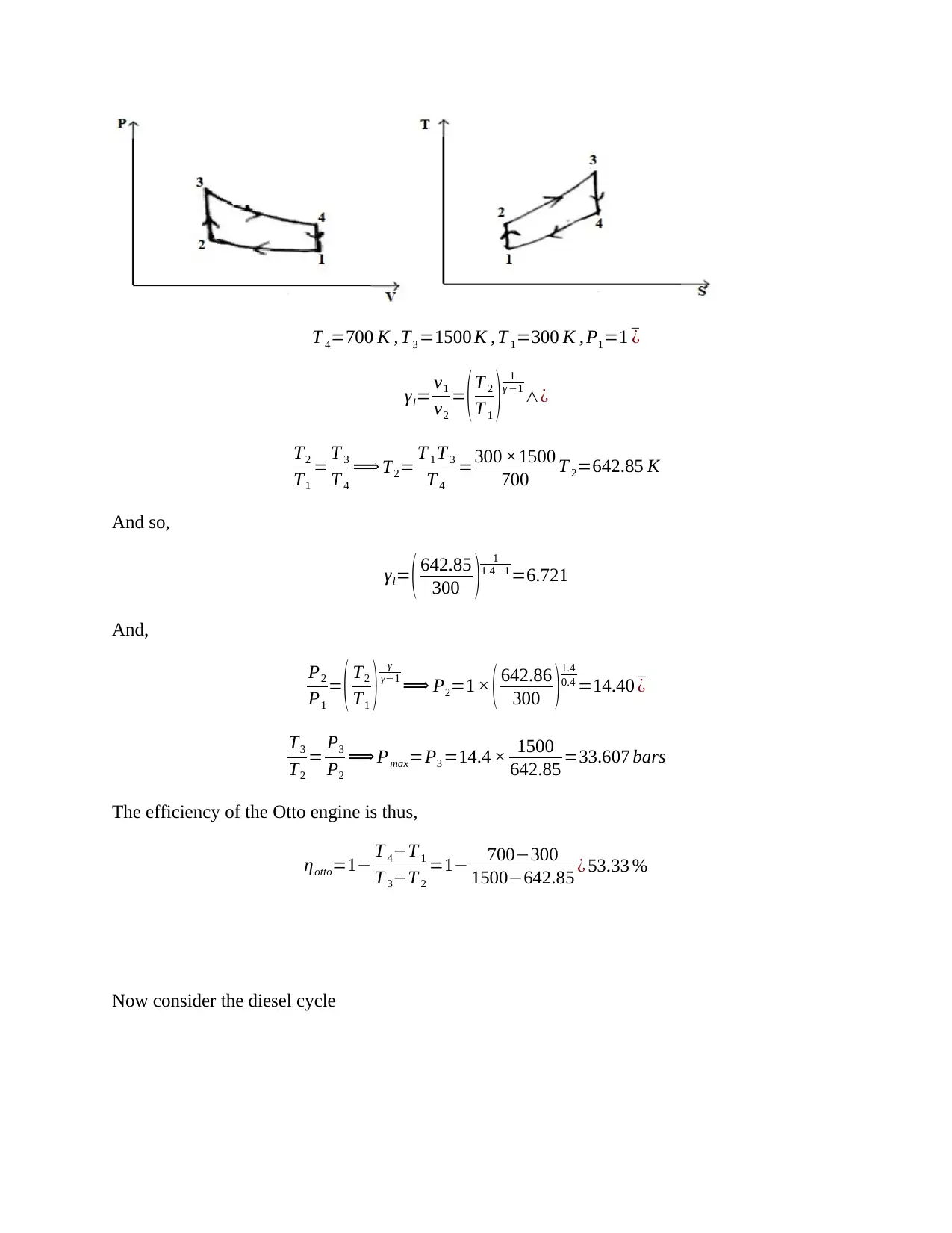
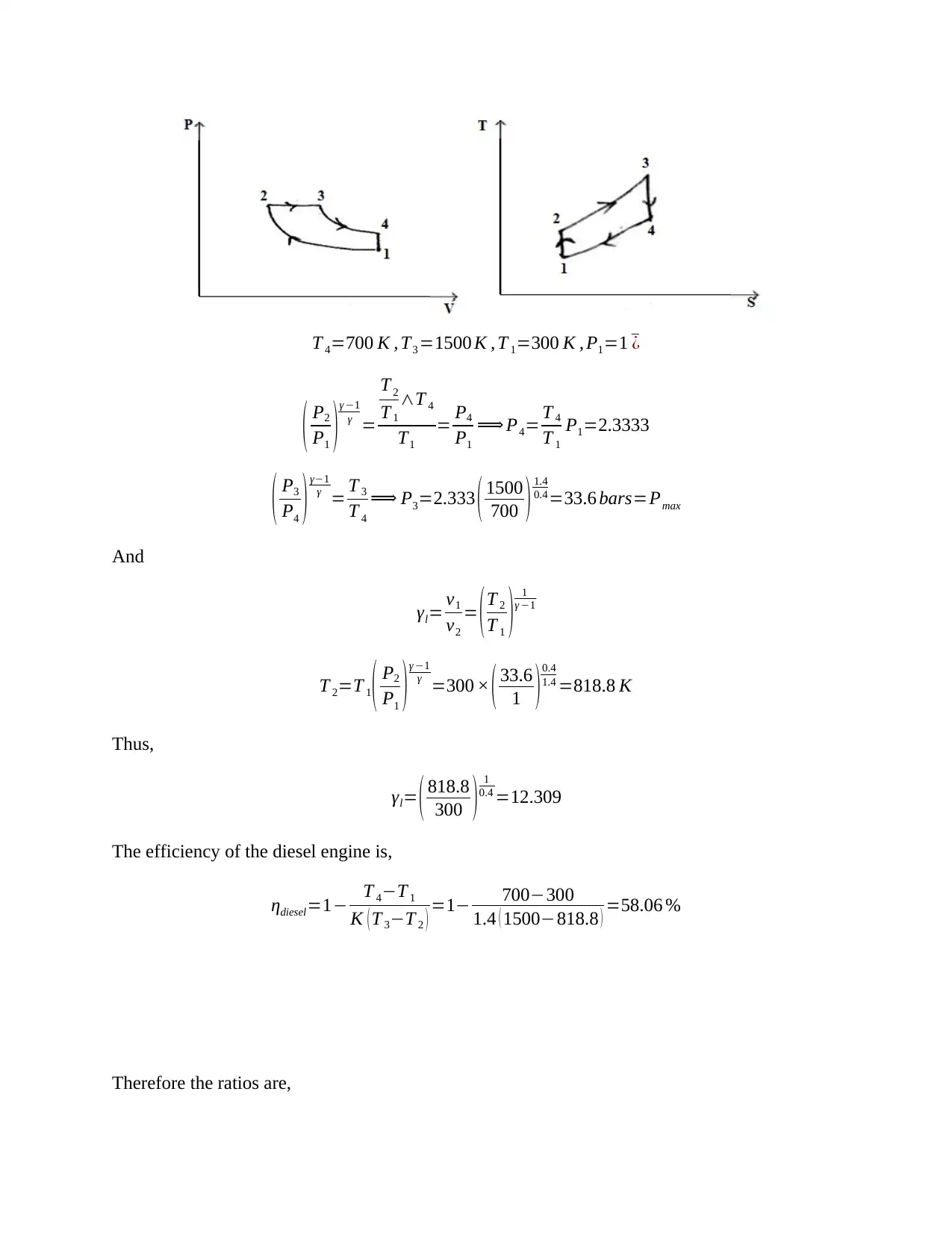
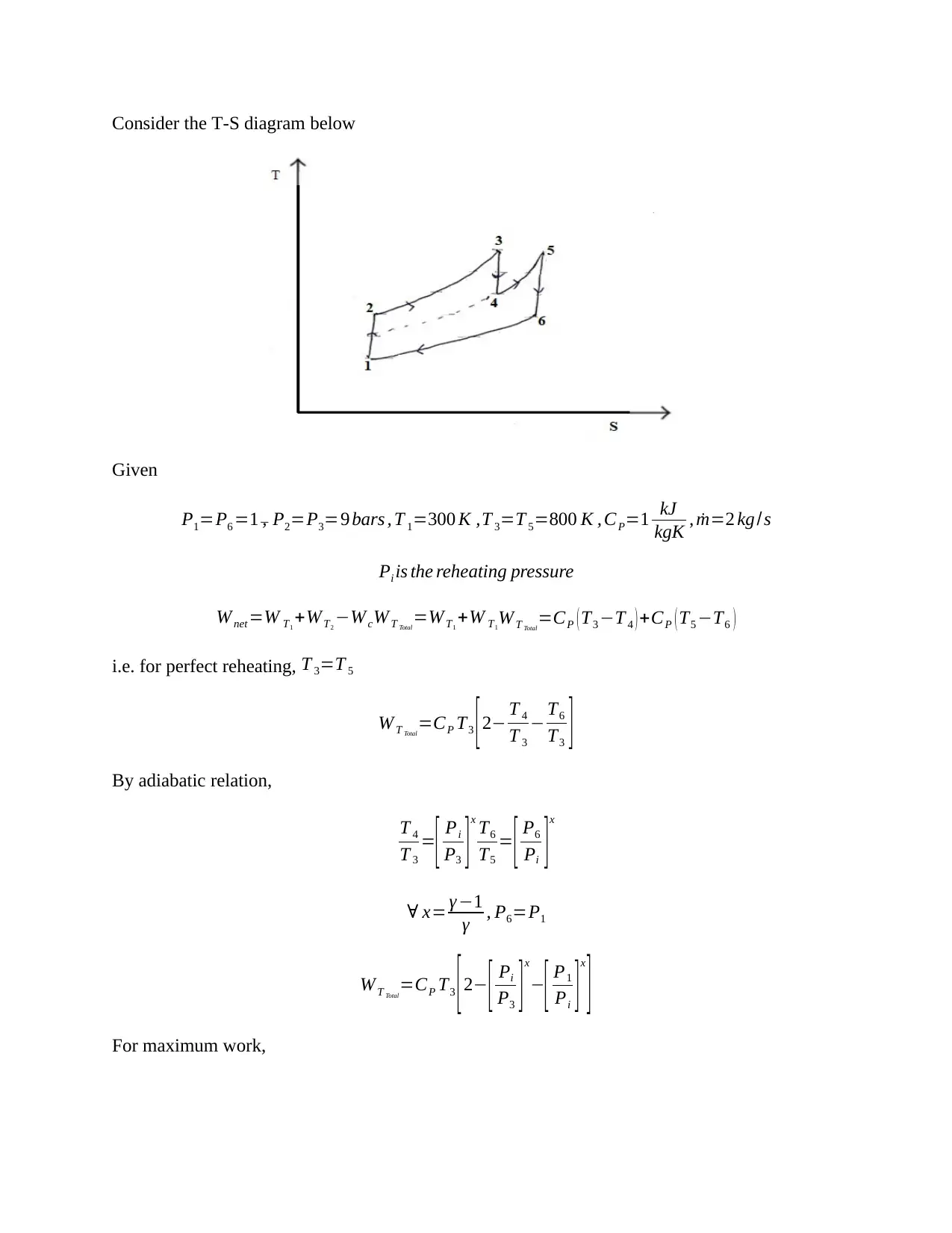
This document presents a detailed solution to a Thermodynamics quiz, addressing key concepts in the field. The solution covers calculations for an ideal dual cycle engine, including pressure and cut-off ratios, heat transfer, work done, and thermal efficiency. It also includes an analysis of Otto and Diesel cycles, determining the ratios of compression ratio, maximum pressure, and efficiency. Furthermore, the solution delves into gas turbine plant analysis, calculating adiabatic relations, and maximum work conditions. Finally, the document includes calculations for engine performance parameters, such as indicated power, thermal efficiency, and air efficiency, for a given engine configuration. This resource is invaluable for students seeking to understand and master the principles of thermodynamics and engine performance.

QUESTION 1
Consider the P-V cycle below
Compression ratio= 16
T1 = 300K
P1 = 1 bar
i) Pressure ratio
( P2
P1 ) γ −1
γ =μγ −1
→ ( P2
P1 )=μγ =161.4
⟹ P2=48.503 bars
μp= P3
P2
=1.443
ii) Cut-off ratio
v1
v2
=16 i. e compression ratio v4
v3
=cut off ratio
v4−v3=0.05( v1−v2)
v4−v2=0.05(v1−v2)
v4
v2
−1=0.05 ( v1
v2
−1 )
¿ 0.05 ( 16−1 )=0.75
Thus,
cut off ratio= v4
v3
=1.75

iii) Mass of air contained in the cylinder
Swept volume=10 litres=10× 10−3 m3
At point 1,
ρ= P
RT = 100
0.287 ×300 =1.16144 kg /m3
Thus mass of air is,
¿ ρ ×V =10× 10−3 ×1.16144 ¿ 0.0116144 kg
iv) Heat added per cycle
μγ −1= T2
T1
T 2=T 1 ×160.4=909.43 K
And
P2= pressure ratio × P1=48.503 bars
For process ( 2−3 ) ,
P2
T2
= P3
T 3
( constant volume )
T 3= 70× 909.43
48.503 =1312.5 K
For process (3-4) (constant pressure)
T3
v3
= T 4
v 4
T 4=1.75 × 1312.5
¿ 2296.875 K
Heat added at constant volume is
q2−3=Cv ( T 3−T 2 )
¿ 0.718 ( 312.5−909.43 )
¿ 289.4 kJ /kg
Heat added at constant pressure is
q3−4=C p ( T 4−T 3 )¿ 1.005 × ( 2296.87−1312.5 ) ¿ 989.29 kJ /kg
Thus, the total heat added is,
¿ 289.4+989.29¿ 1278.69 kJ /kg
Sincem=0.0116144 kg
cycle ,
Q per c ycle=0.0116144 ×1278.69 ¿ 14.8512 kJ /kg

v) Heat rejected per cycle
T 5
T 4
=( 16
1.75 ) 1
0.4
⟹ T5 = T 4
2.42344 =947.77 K
Q5−1
cycle =m ×Cv ( T 5−T 1 )
¿ 0.0116144 × 0.718 ( 947.77−300 )¿ 5.4018 kJ /cycle
vi) Work done per cycle
¿ Qadd−Qrej¿ 14.852−5.4018¿ 9.4502 kJ /cycle
vii) Thermal efficiency of the cycle
η= W
Qadd
¿ 9.4502
14.852 =0.63629¿ 63.629 %
viii) MEP
P ×V = Work
cycle
P= 945.02
10 ×10−3 =9.4502bars
QUESTION 2
Consider the Otto cycle

T 4=700 K , T3 =1500 K , T 1=300 K , P1=1 ¯¿
γl= v1
v2
= (T 2
T 1 ) 1
γ −1 ∧¿
T2
T1
= T 3
T 4
⟹ T2= T 1 T 3
T 4
=300 ×1500
700 T 2=642.85 K
And so,
γl= ( 642.85
300 ) 1
1.4−1 =6.721
And,
P2
P1
= ( T2
T1 ) γ
γ−1 ⟹ P2=1 × ( 642.86
300 ) 1.4
0.4 =14.40 ¯¿
T3
T2
= P3
P2
⟹ Pmax=P3 =14.4 × 1500
642.85 =33.607 bars
The efficiency of the Otto engine is thus,
ηotto=1− T 4−T 1
T 3−T 2
=1− 700−300
1500−642.85 ¿ 53.33 %
Now consider the diesel cycle

T 4=700 K , T3 =1500 K , T 1=300 K , P1=1 ¯¿
( P2
P1 )γ −1
γ =
T 2
T 1
∧T 4
T1
= P4
P1
⟹ P4= T 4
T 1
P1=2.3333
( P3
P4 ) γ−1
γ = T 3
T 4
⟹ P3=2.333 ( 1500
700 ) 1.4
0.4=33.6 bars=Pmax
And
γl= v1
v2
= ( T 2
T 1 ) 1
γ −1
T 2=T 1 ( P2
P1 ) γ −1
γ =300 × ( 33.6
1 ) 0.4
1.4 =818.8 K
Thus,
γl= ( 818.8
300 ) 1
0.4 =12.309
The efficiency of the diesel engine is,
ηdiesel=1− T 4−T 1
K ( T 3−T 2 ) =1− 700−300
1.4 ( 1500−818.8 ) =58.06 %
Therefore the ratios are,

i) Compression ratio
γ= γ l ,otto
γl , diesel
= 6.721
12.309 =0.546
ii) Maximum power
P= Potto
Pdiesel
=33.6
33.6 =1
iii) Efficiency
η= ηotto
ηdiesel
= 53.33
58.06 =0.919
QUESTION 3

Consider the T-S diagram below
Given
P1=P6 =1¯
, P2=P3=9 bars , T 1=300 K ,T 3=T 5=800 K , CP=1 kJ
kgK , ˙m=2 kg /s
Pi is the reheating pressure
W net =W T1
+WT2
−WcWT Total
=WT1
+W T1W T Total
=CP ( T3 −T 4 ) +CP ( T5 −T6 )
i.e. for perfect reheating, T 3=T 5
W T Total
=CP T3 [ 2− T 4
T 3
− T6
T3 ]
By adiabatic relation,
T 4
T 3
=
[ Pi
P3 ]x T6
T5
= [ P6
Pi ] x
∀ x= γ −1
γ , P6=P1
W T Total
=CP T3 [ 2− [ Pi
P3 ] x
−
[ P1
Pi ] x
]
For maximum work,

d ( W TTotal )
d Pi
=0
From the above relation, the condition for maximum work becomes
Pi= √P1 × P2
i.e.
W T 1
=C p ( T 3−T 4 )
By adiabatic relation,
T 4
T 3
=
[ Pi
P3 ]γ −1
γ
[ P3 =P2 ]
T 4=T 3 [ √ P1 × P2
√ P2 × P2 ] γ −1
γ
¿ 800 [ √ 1
9 ] 0.4
1.4
=584.48 K
And so W T 1is,
¿ 1 × ( 800−584.48 )=215.52 kJ /kg
W T 2
=C p ( T 5−T 6 )
By adiabatic relation,
T6
T5
= [ P1
Pi ]γ −1
γ
[ P3=P2 ]
T 6=T 5 [ √ P1 × P1
√ P1 × P2 ]γ−1
γ
=800 [ 1
3 ]0.4
1.4 =584.48 K
And so W T 2is,
¿ 1 × ( 800−584.48 )=215.52 kJ /kg
⟹ W c=C p ( T2−T 1 )
So

T2
T1
= [ P2
P1 ]γ −1
γ
T 2=300 [ 9
1 ]0.4
1.4 =562.0 K
W c=1 ( 562−300 ) =262 kJ / kg
W net (max )=W T1
+WT2
−W c=215.52+215.52−262=169.04 kJ /kg
Maximum power is
Pmax = ˙m× W net ( max ) =2 ×169.04
¿ 338.08 kW
QUESTION 4
Bore, D = 150 mm
Stroke, L = 250 mm
Speed of crankshaft, N =300 rpm
Fuel consumption, mf = 1.2 kg/h
Calorific value, Cv = 39900 kJ/kg
γ=15, ρ=1.8, I.P mep = 5.5 bar
Indicated power I.P is given as

¿ Pmep × vs × N
120 ¿ Pmep × π
4 D2 L × N
120 ¿ 5.5 ×105 × π
4 × ( 0.150 )2 × ( 0.250 ) × 300
120 ¿ 6.075 kW
Thermal efficiency, ηthermis given as
¿ I . P
mf CV
= 6.075
( 1.2
3600 ×39900 ) ¿ 0.457
Air efficiency, ηair is given as
¿ 1− 1 ( ρk −1 )
k ( γk−1 ) ( ρ−1 )
¿ 1− ( 1.81.4−1 )
( 1.4 ) ( 150.4 ) ( 0.8 ) ¿ 0.614
Relative efficiency, ηrelativeis thus
¿ ηtherm
ηair
= 0.457
0.614 ¿ 0.745
ηrelative =74.5 %
QUESTION 5
Dew point temperature = 17.9oC
Wet bulb temperature =22oC
Enthalpy = 65kg/kJ
Specific humidity = 0.013 kg/kg of dry air
Density of air = 1.14 kg/m3