Mechanical Engineering: Heat Transfer Problem - Critical Insulation

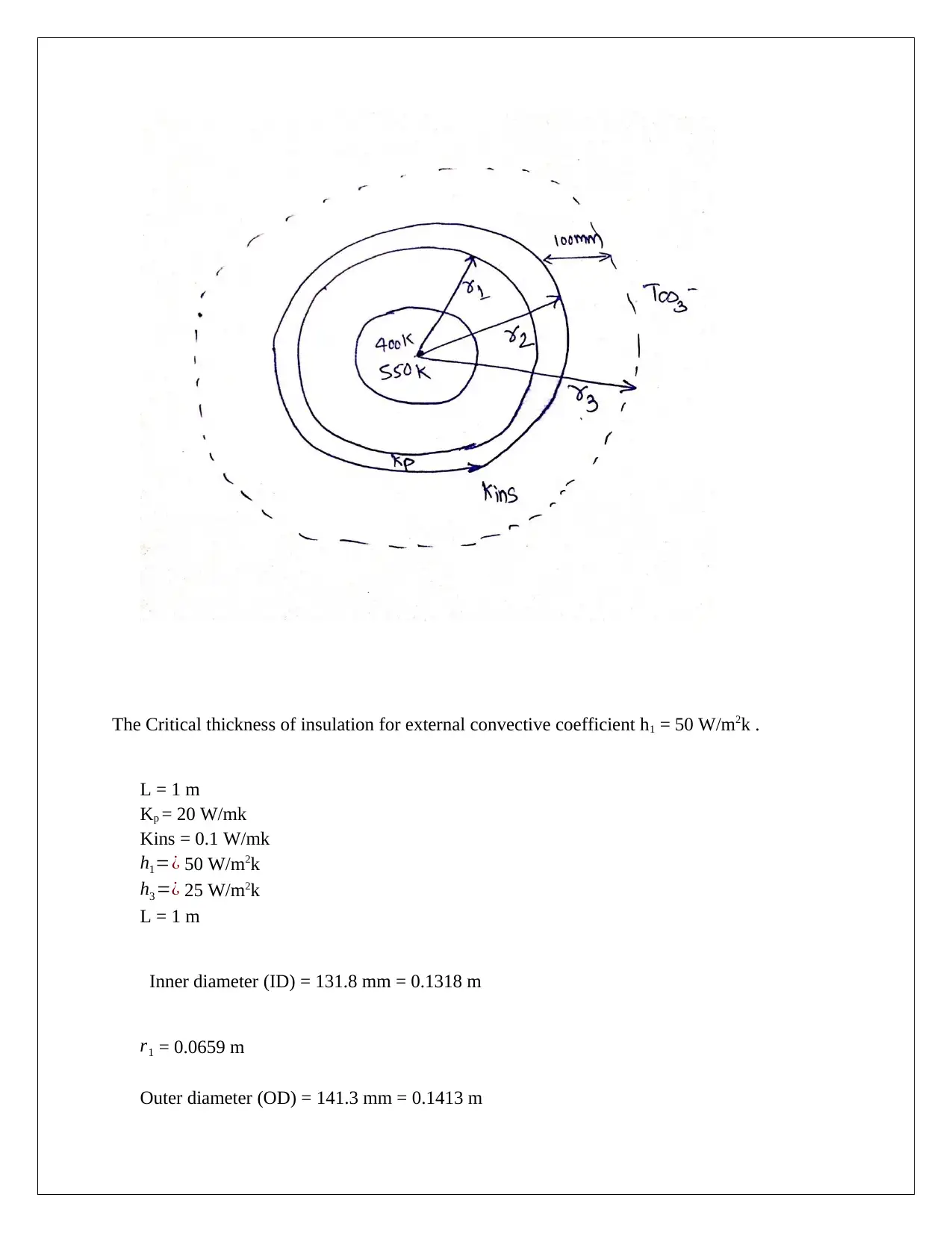
This assignment addresses a heat transfer problem concerning the critical radius of insulation for a cylindrical pipe. The problem defines a scenario where a pipe with a constant surface temperature is insulated with a material of known thermal conductivity, and the surrounding medium is at a lower temperature with a given convective heat transfer coefficient. The solution begins with defining the problem, making necessary assumptions (fixed insulation thickness, negligible air gaps, radiation losses, and series resistances), and applying engineering principles. It explains that for wires with a radius less than the critical radius of insulation, adding insulation can initially increase the heat transfer rate due to a decrease in convection resistance. The core of the solution involves calculating the critical thickness of insulation using given parameters (pipe dimensions, thermal conductivities, and convective heat transfer coefficients). It then calculates the heat transfer rate per meter of pipe with and without insulation, demonstrating how the addition of insulation beyond the critical thickness reduces heat loss. References to relevant literature are also included, supporting the analysis and providing context to the problem-solving approach.

Heat transfer problem
October 13
2018
Critical radius of
Insulation

1.1 Problem definition :
(a) Defining the problem:Let us assume a cylindrical long pipe of outer radius r1with
constant outer surface temperature (T1) .The pipe is now insulated with a material of
thermal conductivity kp . Let us consider that the surrounding medium is at a temperature
T ∞ (T ∞<T1) with convective heat transfer coefficient h.
(b) Assumption :
(i) Insulating thickness fixed.
(ii) All air gaps are considered as neglected.
(iii) Radiations losses are neglected.
(iv) The wall conduction resistance and the air convective resistance are in series.
(v) Assuming value of heat transfer convective coefficient h for hot water is 50
W/m2k and heat is assumed to be uniformly distributed.
(c) Applying Principles of engineering :
For sufficient thin wires whose radius (r) is lesser than critical radius of insulation (rc).
Any insulation wrapped around the wire may result in increase of Heat transfer rate
instead of decreasing it. This happens so because initially when more and more insulation
is being wrapped around the wire there is rapid decrease in convection thermal resistance
as compare to small increase of conduction thermal resistance, the overall effect being
decrease in total thermal resistance and increase of Heat transfer rate .This continuous
happens up to critical radius of insulation beyond which any further insulation added
shall decrease the heat transfer rate.
In case if the radius of wire initially taken is already more than critical radius of
insulation,any insulation wrapped around it shall directly decreases the heat transfer
rate. .
1.2 Problem Formulation :
There are certain situations in engineering design when the objectives is to reduce the flow of
heat i.e. heat exchangers, thermo-flask, building insulations and so on .Thermal insulation
material must have a low thermal conductivity .

Steps for development of model:
(i) For maximum heat dissipation we have to find critical thickness of insulation.
(ii) Rate of heat transfer per meter of pipe.
Insulation saves energy and money every year so it is cost effective.The Insulating a surface
properly requires only initial capital investment, but its effects are impressive and long term.
The payback time of insulation is usually 2.5 years.
1.3 Problem solving approach :

The Critical thickness of insulation for external convective coefficient h1 = 50 W/m2k .
L = 1 m
Kp = 20 W/mk
Kins = 0.1 W/mk
h1=¿ 50 W/m2k
h3 =¿ 25 W/m2k
L = 1 m
Inner diameter (ID) = 131.8 mm = 0.1318 m
r1 = 0.0659 m
Outer diameter (OD) = 141.3 mm = 0.1413 m

r2 = 0.0659 m + (0.1413/2) m =0.0659 + 0.07065 = 0.13655 m
r3 = r2 + t = 0.13655 + 0.1 = 0.23655 m
(Critical thickness of insulation) rc = k p
h 1 = 20
50 = 0.4 m = 400 mm
Q= T ∞ 1−T ∞ 3
Rt h
Here,
T ∞ 1−T ∞ 3=600K
Rth ¿ 1
h1 (2 π r1 L) +
ln r 2
r 1
2 π k p L +
ln r3
r 1
2 π kins L + 1
h3 ( 2 π r3 L)
Rth ¿ 1
50(2 π × 0.0659× 1) +
ln 0.40
0.13655
2 π × 20 ×1 +
ln 0.23655
0.13655
2 π × 0.1× 1 + 1
25(2 π × 0.23655× 1)
Rth = 0.957
Q= 600
0.957 W/m
Q=¿626. 95 W/m
r1 = 0.0659 m
r3= rc = 0.40 m

Rth(new) ¿ 1
h1 (2 π r1 L)+
ln r 2
r 1
2 π k p L +
ln r c
r 1
2 π kins L + 1
h3 (2 π rc L)
Rth(new) ¿ 1
50(2 π × 0.0659× 1) +
ln 0.40
0.13655
2 π × 20 ×1 +
ln 0.40
0.13655
2 π × 0.1× 1 + 1
25(2 π × 0.40 ×1)
Rth(new) = 1.782
Q= 600
1.782 = 336.70 W/m
Note: It is important that the addition of further insulation the critical thickness decrease the
value of heat loss (Q) .
References :
Aziz, A. (1997). The critical thickness of insulation. Heat transfer engineering, 18(2), 61-91.
Simmons, L.D., 1976. Critical thickness of insulation accounting for variable convection
coefficient and radiation loss. Journal of Heat Transfer, 98(1), pp.150-151.