Stress Analysis Assignment: Mechanical Engineering Fundamentals
VerifiedAdded on 2019/09/23
|10
|467
|172
Homework Assignment
AI Summary
This assignment solution addresses stress analysis problems in mechanical engineering. The solution covers stress at points A and B, calculating maximum in-plane shear stress, principal stresses, and determining if yielding occurs. It also includes an analysis of a test specimen under compressive stress, calculating strain and presenting the strain tensor. Additionally, the solution uses the finite element method to analyze a plate, including element stiffness matrices, global stiffness matrices, and force vectors, and compares the results with calculative methods. The assignment demonstrates the application of key concepts in stress analysis, including the use of finite element analysis for mechanical engineering problems.

Answer (2)
Given data:
ri=0.5 m, di=1 m
r 0=0.52 m, d 0=1.04 m
P=100 bars
t=r 0−ri=0.52−0.50=0.02m
k = ro
ri = 0.52
0.50 =1.04
Stress at point (A)
Internal pressure,
Axial tension σx 1= p a
2 t =100 x 0.52
0.04 =1300 N
m 2
Hoop tension σy= p a
t =100 x 0.52
0.02 =2600 N
m2
Axial compression
Axial Normal stress σx 2= P
( k2−1 ) = 100
( 1.042−1 ) =1225.4901 N
m 2
Twisting moment:
Maximum out-plane shear stress, τ = Pr
2t = 100 x 0.52
0.04 =1300 N
m 2
Answer (a)
State of stress:
σx=σx 1+σx 2=1300+1225.5=2525.2 N
m2
σy=2600 N
m2
τ xy=1300 N
m2
σ Z=τ yz =τ xz=0
The maximum in-plane shear stress:
τ xy= √ ( σ x−σ y
2 )2
+ τxy
2= √1387.56+1690000=1300.50 N
m 2
1 | P a g e
Given data:
ri=0.5 m, di=1 m
r 0=0.52 m, d 0=1.04 m
P=100 bars
t=r 0−ri=0.52−0.50=0.02m
k = ro
ri = 0.52
0.50 =1.04
Stress at point (A)
Internal pressure,
Axial tension σx 1= p a
2 t =100 x 0.52
0.04 =1300 N
m 2
Hoop tension σy= p a
t =100 x 0.52
0.02 =2600 N
m2
Axial compression
Axial Normal stress σx 2= P
( k2−1 ) = 100
( 1.042−1 ) =1225.4901 N
m 2
Twisting moment:
Maximum out-plane shear stress, τ = Pr
2t = 100 x 0.52
0.04 =1300 N
m 2
Answer (a)
State of stress:
σx=σx 1+σx 2=1300+1225.5=2525.2 N
m2
σy=2600 N
m2
τ xy=1300 N
m2
σ Z=τ yz =τ xz=0
The maximum in-plane shear stress:
τ xy= √ ( σ x−σ y
2 )2
+ τxy
2= √1387.56+1690000=1300.50 N
m 2
1 | P a g e
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Answer (b)
Principal stresses:
σ 1= σ x +σ y
2 + √ ( σ x−σ y
2 )2
+τ xy
2
¿ 2525.2+ 2600
2 +¿1300.50
¿ 3863.1 N /m2
σ 2= σx +σ y
2 − √ ( σ x−σ y
2 )2
+ τxy
2
¿ 2525.2+2600
2 −1300.50
σ 2=1261.7 N
m 2
σ 3=0
Answer (c)
τ max= ( σ 1−σ 3 )
2 =3863.1
2 =1931.55 N
m2
Yielding not occur because maximum shear stress less than yield stress.
Stress at point (B)
Internal pressure,
Axial tension σx 1= p a
2 t =100 x 0.50
0.04 =1200 N
m 2
Hoop tension σy= p a
t =100 x 0.50
0.02 =2500 N
m2
Twisting moment:
Maximum out-plane shear stress, τ = Pr
4 t = 100 x 0.50
0.04 =625 N
m2
Answer (A)
State of stress:
2 | P a g e
Principal stresses:
σ 1= σ x +σ y
2 + √ ( σ x−σ y
2 )2
+τ xy
2
¿ 2525.2+ 2600
2 +¿1300.50
¿ 3863.1 N /m2
σ 2= σx +σ y
2 − √ ( σ x−σ y
2 )2
+ τxy
2
¿ 2525.2+2600
2 −1300.50
σ 2=1261.7 N
m 2
σ 3=0
Answer (c)
τ max= ( σ 1−σ 3 )
2 =3863.1
2 =1931.55 N
m2
Yielding not occur because maximum shear stress less than yield stress.
Stress at point (B)
Internal pressure,
Axial tension σx 1= p a
2 t =100 x 0.50
0.04 =1200 N
m 2
Hoop tension σy= p a
t =100 x 0.50
0.02 =2500 N
m2
Twisting moment:
Maximum out-plane shear stress, τ = Pr
4 t = 100 x 0.50
0.04 =625 N
m2
Answer (A)
State of stress:
2 | P a g e

σx=1200 N
m2
σy=2500 N
m2
τ xy=625 N
m2
σ Z=τ yz =τ xz=0
The maximum in-plane shear stress:
τ xy= √ ( σ x−σ y
2 )2
+ τxy
2= √1387.56+1690000=901.73 N
m2
Answer (B)
Principal stresses:
σ 1= 1200+2500
2 + √ ( σ x−σ y
2 )
2
+τ xy
2
¿ 1850+901.73
¿ 2751.73 N / m2
σ 2= σx +σ y
2 − √ ( σ x−σ y
2 )2
+ τxy
2
¿ 1850−901.73
σ 2=948.27 N
m2
σ 3=0
Answer(c)
τ max= ( σ 1−σ 3 )
2 =2751.73
2 =1375.865 N
m2
Shear stress of given cylinder lower then yield stress, so yielding not occur.
3 | P a g e
m2
σy=2500 N
m2
τ xy=625 N
m2
σ Z=τ yz =τ xz=0
The maximum in-plane shear stress:
τ xy= √ ( σ x−σ y
2 )2
+ τxy
2= √1387.56+1690000=901.73 N
m2
Answer (B)
Principal stresses:
σ 1= 1200+2500
2 + √ ( σ x−σ y
2 )
2
+τ xy
2
¿ 1850+901.73
¿ 2751.73 N / m2
σ 2= σx +σ y
2 − √ ( σ x−σ y
2 )2
+ τxy
2
¿ 1850−901.73
σ 2=948.27 N
m2
σ 3=0
Answer(c)
τ max= ( σ 1−σ 3 )
2 =2751.73
2 =1375.865 N
m2
Shear stress of given cylinder lower then yield stress, so yielding not occur.
3 | P a g e
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Answer (3):
StrainTensor= [εxx εxy εxz
εyx εyy εyz
εzx εzy εzz ]
¿
[ ∂ u
∂ x
1
2 ( ∂u
∂ y + ∂ v
∂ x ) 1
2 ( ∂ u
∂ z + ∂ w
∂ x )
1
2 ( ∂ u
∂ y + ∂ v
∂ x ) ∂ v
∂ y
1
2 ( ∂ v
∂ z + ∂ w
∂ y )
1
2 ( ∂u
∂ z + ∂ w
∂ x ) 1
2 ( ∂ v
∂ z + ∂ w
∂ y ) ∂ w
∂ z ]Assume 1mm pressed after applied vertical force,
So the strain in vertical direction = change∈lenght
originallenght = 1
1000 =0.001
Whereas die fixed test specimen in horizontal direction and Z-direction.
Therefore specimen cannot expand in X and Z direction or X1 and X3 direction.
The remaining component values are 1.
StrainTensor L= [ 0.001 0.0005 0
0.0005 1 0.0005
0 0.0005 1 ]
Answer (B)
f ( k ) =l
f ( x 2 )=x 1
The above equation mention that when die compresses test specimen the expansion of
specimen in two perpendicular direction. As per basic fundamental of strain change length
from original length. But for this case the specimen length change in two direction. As per
given formula the change in length in l direction have change also in k direction.
4 | P a g e
StrainTensor= [εxx εxy εxz
εyx εyy εyz
εzx εzy εzz ]
¿
[ ∂ u
∂ x
1
2 ( ∂u
∂ y + ∂ v
∂ x ) 1
2 ( ∂ u
∂ z + ∂ w
∂ x )
1
2 ( ∂ u
∂ y + ∂ v
∂ x ) ∂ v
∂ y
1
2 ( ∂ v
∂ z + ∂ w
∂ y )
1
2 ( ∂u
∂ z + ∂ w
∂ x ) 1
2 ( ∂ v
∂ z + ∂ w
∂ y ) ∂ w
∂ z ]Assume 1mm pressed after applied vertical force,
So the strain in vertical direction = change∈lenght
originallenght = 1
1000 =0.001
Whereas die fixed test specimen in horizontal direction and Z-direction.
Therefore specimen cannot expand in X and Z direction or X1 and X3 direction.
The remaining component values are 1.
StrainTensor L= [ 0.001 0.0005 0
0.0005 1 0.0005
0 0.0005 1 ]
Answer (B)
f ( k ) =l
f ( x 2 )=x 1
The above equation mention that when die compresses test specimen the expansion of
specimen in two perpendicular direction. As per basic fundamental of strain change length
from original length. But for this case the specimen length change in two direction. As per
given formula the change in length in l direction have change also in k direction.
4 | P a g e
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
[ ∂ u
∂ x 1
1
2 ( ∂u
∂ x 2 + ∂ v
∂ x 1 ) 1
2 ( ∂ u
∂ x 3 + ∂ w
∂ x 1 )
1
2 ( ∂ u
∂ x 2 + ∂ v
∂ x 1 ) ∂ v
∂ x 2
1
2 ( ∂ v
∂ x 3 + ∂ w
∂ x 2 )
1
2 ( ∂ u
∂ x 3 + ∂ w
∂ x 1 ) 1
2 ( ∂ v
∂ x 3 + ∂ w
∂ x 2 ) ∂ w
∂ x 3
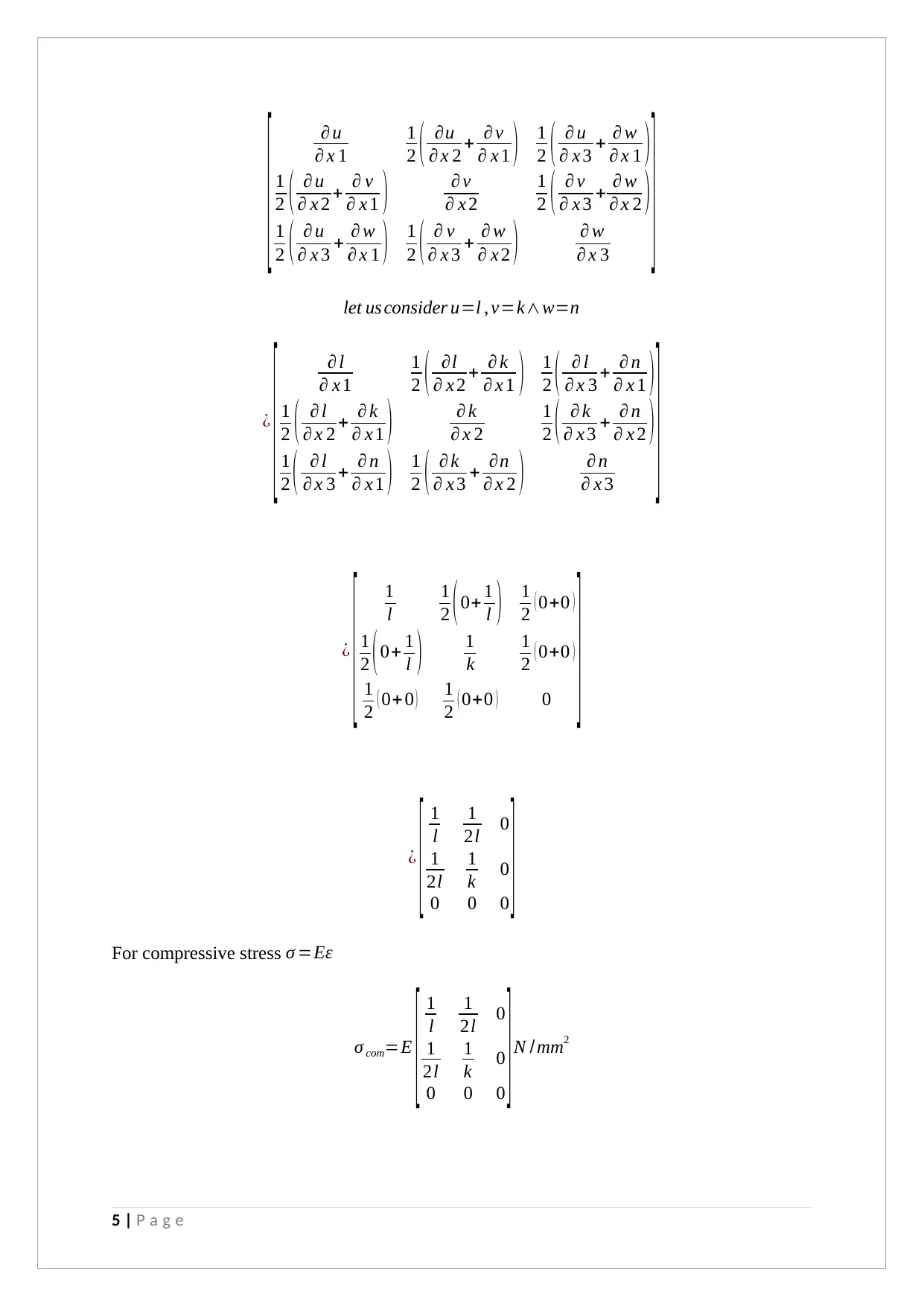
]let us consider u=l , v=k∧w=n
¿
[ ∂ l
∂ x 1
1
2 ( ∂l
∂ x 2 + ∂ k
∂ x 1 ) 1
2 ( ∂ l
∂ x 3 + ∂ n
∂ x 1 )
1
2 ( ∂ l
∂ x 2 + ∂ k
∂ x 1 ) ∂ k
∂ x 2
1
2 ( ∂ k
∂ x 3 + ∂ n
∂ x 2 )
1
2 ( ∂ l
∂ x 3 + ∂ n
∂ x 1 ) 1
2 ( ∂ k
∂ x 3 + ∂n
∂ x 2 ) ∂ n
∂ x 3
]
¿
[ 1
l
1
2 (0+ 1
l ) 1
2 ( 0+0 )
1
2 (0+ 1
l ) 1
k
1
2 ( 0+0 )
1
2 ( 0+0 ) 1
2 ( 0+0 ) 0 ]
¿
[ 1
l
1
2l 0
1
2l
1
k 0
0 0 0 ]
For compressive stress σ =Eε
σ com=E
[ 1
l
1
2l 0
1
2l
1
k 0
0 0 0 ] N /mm2
5 | P a g e
∂ x 1
1
2 ( ∂u
∂ x 2 + ∂ v
∂ x 1 ) 1
2 ( ∂ u
∂ x 3 + ∂ w
∂ x 1 )
1
2 ( ∂ u
∂ x 2 + ∂ v
∂ x 1 ) ∂ v
∂ x 2
1
2 ( ∂ v
∂ x 3 + ∂ w
∂ x 2 )
1
2 ( ∂ u
∂ x 3 + ∂ w
∂ x 1 ) 1
2 ( ∂ v
∂ x 3 + ∂ w
∂ x 2 ) ∂ w
∂ x 3
]let us consider u=l , v=k∧w=n
¿
[ ∂ l
∂ x 1
1
2 ( ∂l
∂ x 2 + ∂ k
∂ x 1 ) 1
2 ( ∂ l
∂ x 3 + ∂ n
∂ x 1 )
1
2 ( ∂ l
∂ x 2 + ∂ k
∂ x 1 ) ∂ k
∂ x 2
1
2 ( ∂ k
∂ x 3 + ∂ n
∂ x 2 )
1
2 ( ∂ l
∂ x 3 + ∂ n
∂ x 1 ) 1
2 ( ∂ k
∂ x 3 + ∂n
∂ x 2 ) ∂ n
∂ x 3
]
¿
[ 1
l
1
2 (0+ 1
l ) 1
2 ( 0+0 )
1
2 (0+ 1
l ) 1
k
1
2 ( 0+0 )
1
2 ( 0+0 ) 1
2 ( 0+0 ) 0 ]
¿
[ 1
l
1
2l 0
1
2l
1
k 0
0 0 0 ]
For compressive stress σ =Eε
σ com=E
[ 1
l
1
2l 0
1
2l
1
k 0
0 0 0 ] N /mm2
5 | P a g e

Answer (C)
As given m = 9500mm so the change in length = 500mm so that following strain
tensor obtained
ε = 500
1000 =0.5
Following matrix obtained
ε ij= [ 0.5 0.25 0.25
0.25 1 0
0.25 0 1 ]
σ =ε ij E
Converting into meter and obtained following equation
¿ 1000 x [ 0.5 0.25 0.25
0.25 1 0
0.25 0 1 ]
σ ij= [ 500 250 250
250 1000 0
0 25 1000 ] N /mm 2
F=σ x 1 x 1 x Area
Fx 1 x 1=500 x ( 10 x 10 )
Fx 1 x 1=50000 N
Answer (4):
Using two element each of 50 mm long in length, the finite element model in figure below. Nodes
and elements are numbered as shown. Noted that the area at the mid-point of the plate is as
discussed following:
6 | P a g e
As given m = 9500mm so the change in length = 500mm so that following strain
tensor obtained
ε = 500
1000 =0.5
Following matrix obtained
ε ij= [ 0.5 0.25 0.25
0.25 1 0
0.25 0 1 ]
σ =ε ij E
Converting into meter and obtained following equation
¿ 1000 x [ 0.5 0.25 0.25
0.25 1 0
0.25 0 1 ]
σ ij= [ 500 250 250
250 1000 0
0 25 1000 ] N /mm 2
F=σ x 1 x 1 x Area
Fx 1 x 1=500 x ( 10 x 10 )
Fx 1 x 1=50000 N
Answer (4):
Using two element each of 50 mm long in length, the finite element model in figure below. Nodes
and elements are numbered as shown. Noted that the area at the mid-point of the plate is as
discussed following:
6 | P a g e
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

A ( x )= A ( 0 ) (1− x
2 L )
A 1 ( 0 )=10 mm2
L=100 mm
Let us take area X = L,
A ( L )=10 (1− 1
2 )
A 2 ( L )=5 mm 2
So, the area at mid span A 3= A 1+ A 2
2 =10+5
2 = 7.5mm2
Area of top most ¿ position= 10+7.5
2 =8.75 mm 2
Area of bottom most position= 7.5+5
2 =6.25 mm 2
Boundary condition F 1=0 , F 3=1 N
Element stiffness matrix Ke= EA
L [ 1 −1
−1 1 ]
K1= 1000 x 8.75
50 [ 1 −1
−1 1 ]
K2= 1000 x 6.25
50 [ 1 −1
−1 1 ]
The global stiffness matrix K assembled
K= 1000
50 [ 1 −8.75 0
−8.75 15 −6.25
0 −6.25 6.25 ]
The element body force vector are
Fe= Alρ
2 [1
1 ]
F1= 8.75 x 50 x 1000
2 [1
1 ]
F2=6.25 x 50 x 1000
2 [ 1
1 ]
7 | P a g e
2 L )
A 1 ( 0 )=10 mm2
L=100 mm
Let us take area X = L,
A ( L )=10 (1− 1
2 )
A 2 ( L )=5 mm 2
So, the area at mid span A 3= A 1+ A 2
2 =10+5
2 = 7.5mm2
Area of top most ¿ position= 10+7.5
2 =8.75 mm 2
Area of bottom most position= 7.5+5
2 =6.25 mm 2
Boundary condition F 1=0 , F 3=1 N
Element stiffness matrix Ke= EA
L [ 1 −1
−1 1 ]
K1= 1000 x 8.75
50 [ 1 −1
−1 1 ]
K2= 1000 x 6.25
50 [ 1 −1
−1 1 ]
The global stiffness matrix K assembled
K= 1000
50 [ 1 −8.75 0
−8.75 15 −6.25
0 −6.25 6.25 ]
The element body force vector are
Fe= Alρ
2 [1
1 ]
F1= 8.75 x 50 x 1000
2 [1
1 ]
F2=6.25 x 50 x 1000
2 [ 1
1 ]
7 | P a g e
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

The force applied
F1= 8.75 x 50 x 1000
2 [1
1 ]
F1=[ 0.218750
0.218750 ]
F2=6.25 x 50 x 1000
2 [ 1
1 ]
F2=
[0.156250
0.156250 ]
The global load vector F is assembled from f 1 , f 2 and the point load F = 1N added
F= [ 0.218750
0.37500
1.15625 ]
Now using formula in order to obtained displacement F=kx
1000
50 [ 1 −8.75 0
−8.75 15 −6.25
0 −6.25 6.25 ][u 1
u 2
u 3 ]= [0.218750
0.37500
1.15625 ]
sinceu 1=0 due ¿ ¿ postion of vertical rod , eliminate first raw∧first coloum
1000 x 6.25
50 [ 15 −6.25
−6.25 6.25 ][u 2
u3 ]= [ 0.375
1.15625 ]
Solving above ¿
u 2=1.4 mm
u 3=3.35952 mm
To obtain stress
σ =EBq
σ 1=1000 x 1
50 [ −1 1 ] [ 0
1.4 ] =28 N
mm 2
σ 2=1000 x 1
50 [ −1 1 ] [ 1.4
3.35952 ]=39.1904 N
mm 2
8 | P a g e
F1= 8.75 x 50 x 1000
2 [1
1 ]
F1=[ 0.218750
0.218750 ]
F2=6.25 x 50 x 1000
2 [ 1
1 ]
F2=
[0.156250
0.156250 ]
The global load vector F is assembled from f 1 , f 2 and the point load F = 1N added
F= [ 0.218750
0.37500
1.15625 ]
Now using formula in order to obtained displacement F=kx
1000
50 [ 1 −8.75 0
−8.75 15 −6.25
0 −6.25 6.25 ][u 1
u 2
u 3 ]= [0.218750
0.37500
1.15625 ]
sinceu 1=0 due ¿ ¿ postion of vertical rod , eliminate first raw∧first coloum
1000 x 6.25
50 [ 15 −6.25
−6.25 6.25 ][u 2
u3 ]= [ 0.375
1.15625 ]
Solving above ¿
u 2=1.4 mm
u 3=3.35952 mm
To obtain stress
σ =EBq
σ 1=1000 x 1
50 [ −1 1 ] [ 0
1.4 ] =28 N
mm 2
σ 2=1000 x 1
50 [ −1 1 ] [ 1.4
3.35952 ]=39.1904 N
mm 2
8 | P a g e

Answer (b)
X = 50 mm, at mid span.
A ( 50 ) = A ( 0 ) ( 1− 50
200 )
¿ 10 ( 0.75 )
A ( 50 )=7.5 mm 2
A ( x )= A ( 0 ) (1− x
2 L )
A ( L )=10 (1− L
2 L )
¿ 5 mm 2
Lets take x = 99 mm
A ( 99 ) =A ( 0 ) (1− 99
2 x 100 )
¿ 10 ( 0.505 )
¿ 5.05 mm
σ = ρg ( L−x )
2 ( 1+ A ( L )
A ( x ) )
¿ ρg ( 100−50 )
2 ( 1+ A ( L )
A ( 0 ) )
¿ ρg ( 100−50 )
2 (1+ 5
10 )
σ =ρg ( 37.5 )
¿ 1000 x 9.8 x (37.5)
σ =36.75 N / mm 2
σ = ρg (100−99 )
2 (1+ A ( L )
A ( 99 ) )
¿ ρg ( 100−99 )
2 ( 1+ 5
5.05 )
ρg (100−99 )
2 (1.99 )
1000 x 10 x ( 1 )
2 ( 1.99 )
9 | P a g e
X = 50 mm, at mid span.
A ( 50 ) = A ( 0 ) ( 1− 50
200 )
¿ 10 ( 0.75 )
A ( 50 )=7.5 mm 2
A ( x )= A ( 0 ) (1− x
2 L )
A ( L )=10 (1− L
2 L )
¿ 5 mm 2
Lets take x = 99 mm
A ( 99 ) =A ( 0 ) (1− 99
2 x 100 )
¿ 10 ( 0.505 )
¿ 5.05 mm
σ = ρg ( L−x )
2 ( 1+ A ( L )
A ( x ) )
¿ ρg ( 100−50 )
2 ( 1+ A ( L )
A ( 0 ) )
¿ ρg ( 100−50 )
2 (1+ 5
10 )
σ =ρg ( 37.5 )
¿ 1000 x 9.8 x (37.5)
σ =36.75 N / mm 2
σ = ρg (100−99 )
2 (1+ A ( L )
A ( 99 ) )
¿ ρg ( 100−99 )
2 ( 1+ 5
5.05 )
ρg (100−99 )
2 (1.99 )
1000 x 10 x ( 1 )
2 ( 1.99 )
9 | P a g e
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

σ =99.50 N /mm 2
The finite element method and other calculative method have different answer because finite
element consider behaviour at the element level whereas number of elements increasing more
accurate results obtained. In calculative method considering entire body and so that results may
varies from finite element method.
10 | P a g e
The finite element method and other calculative method have different answer because finite
element consider behaviour at the element level whereas number of elements increasing more
accurate results obtained. In calculative method considering entire body and so that results may
varies from finite element method.
10 | P a g e
1 out of 10
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





