Mechanical Vibrations Assignment Solution, Semester 1, University Name

This assignment solution covers several key topics in mechanical vibrations. It begins by analyzing forces and solving equations of motion, then proceeds to calculate natural and damped frequencies for rigid frames. The solution further delves into the application of Laplace transforms and the derivation of particular solutions for specific forcing functions. It also examines the dynamics of a system with a spring, damper, and mass, providing a detailed breakdown of the forces involved and the resulting equations of motion. Finally, the assignment explores the behavior of a system involving a pendulum and a mass, deriving the natural frequencies and solving for constants within the system. The solution includes a bibliography citing relevant sources for further study.

1
Mechanical Vibrations
Student’s Name
Institutional Affiliation
Date

2
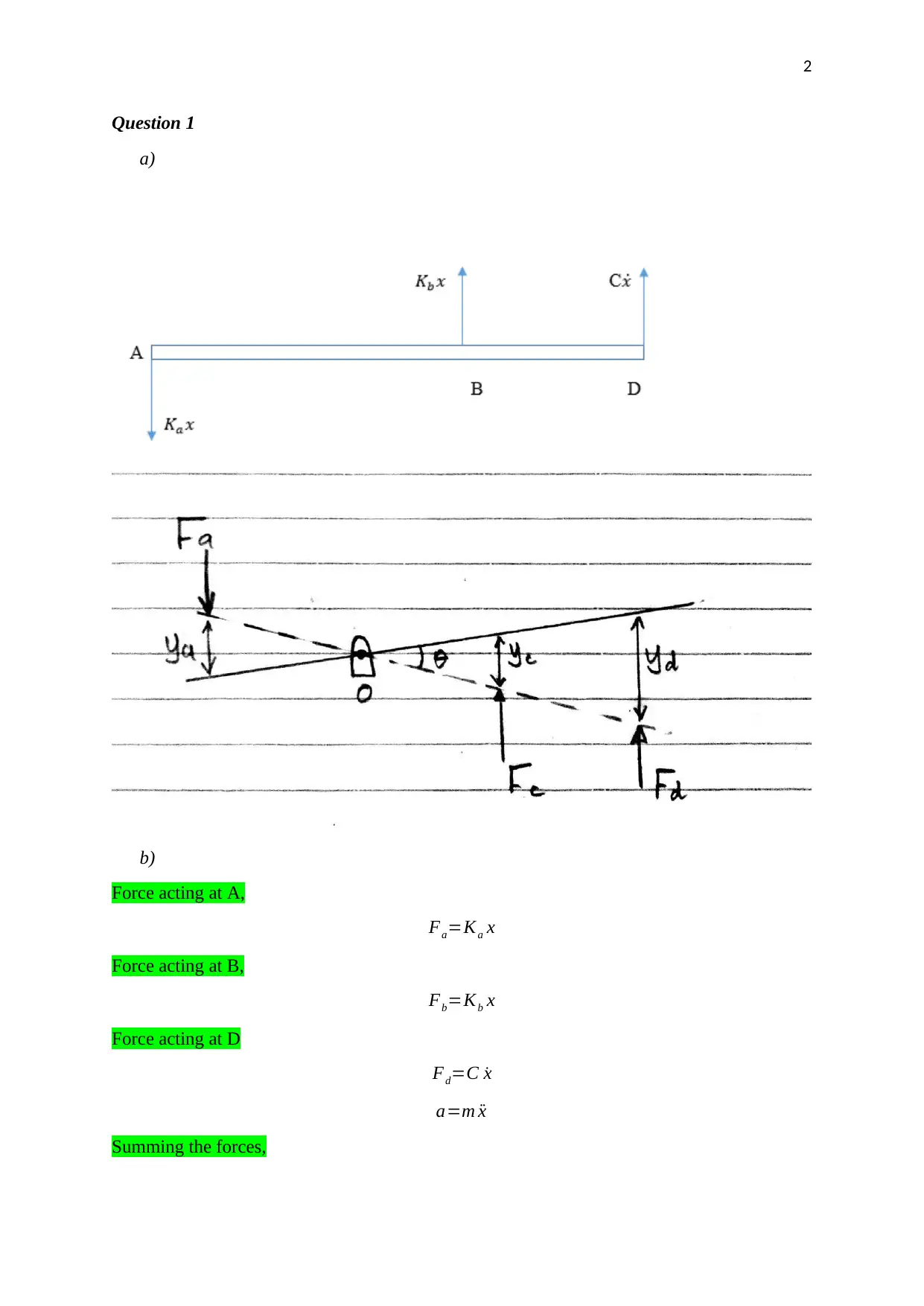
Question 1
a)
b)
Force acting at A,
Fa=Ka x
Force acting at B,
Fb=Kb x
Force acting at D
Fd=C ˙x
a=m ¨x
Summing the forces,

3
Fd +Fb=Fa
m ¨x +C ˙x +Kb x=Ka x
m ¨x +C ˙x + Kb x−Ka x=0
m ¨x +C ˙x + ( K b−Ka ) x=0
10 ¨x+ 200 ˙x + ( 150−53 ) x=0
10 ¨x+ 200 ˙x +97 x=0
c)
∑ T =Io ¨θ
−a Fa−b Fb−L Fd=I o ¨θ
−Ka a ( ya ) −Kb a ( yb ) b−CL ( ˙yd )= ( mL2 ) ¨θ
Where,
I o=mk2=mL2
ya=aθ
yb=bθ
yd =Lθ
−Ka a2 θ−Kb b2 θ−C L2 ˙θ=mL2 ¨θ
mL2 ¨θ+C L2 ˙θ+ ( Ka a2 + Kb b2 ) θ=0
Substituting the given values we have,
10( 0.3)2 ¨θ+200(0.3)2 ˙θ+ (53( 0.2)2 +150(0.1)2 ) θ=0
0.9 ¨θ+18 ˙θ+3.62 θ=0
d)
Solving the equation of motion,
0.9 ¨θ+18 ˙θ+3.62 θ=0
θ=−b ± √b2 −4 ac
2 a , a=0.9, b=18 , c=3.62
θ=−18 ± √182−4 (0.9)(3.62)
1.8

4
θ=−18 ± √324−13.032
1.8
θ=−18 ± 17.63
1.8
θ=−19.79∨−0.21
Solution,
θ ( t )=c1 e−19.79t +c2 e−0.21 t
θ ( 0 ) =c1+ c2=15
˙θ ( t )=−19.79 c1 e−19.79 t −0.21 c2 e−0.21 t
˙θ ( 0 ) =−19.79 c1−0.21 c2=0
19.79 c1 +0.21 c2=0
c2=94.24 c1
From,
c1 +c2=15
c1 +94.24 c1=15
95.24 c1 =15
c1=0.1575
c2=94.24 ( 0.1575 ) =14.8428
θ ( t ) =0.1575 e−19.79 t +14.8428 e−0.21 t
Question 2
i.

5
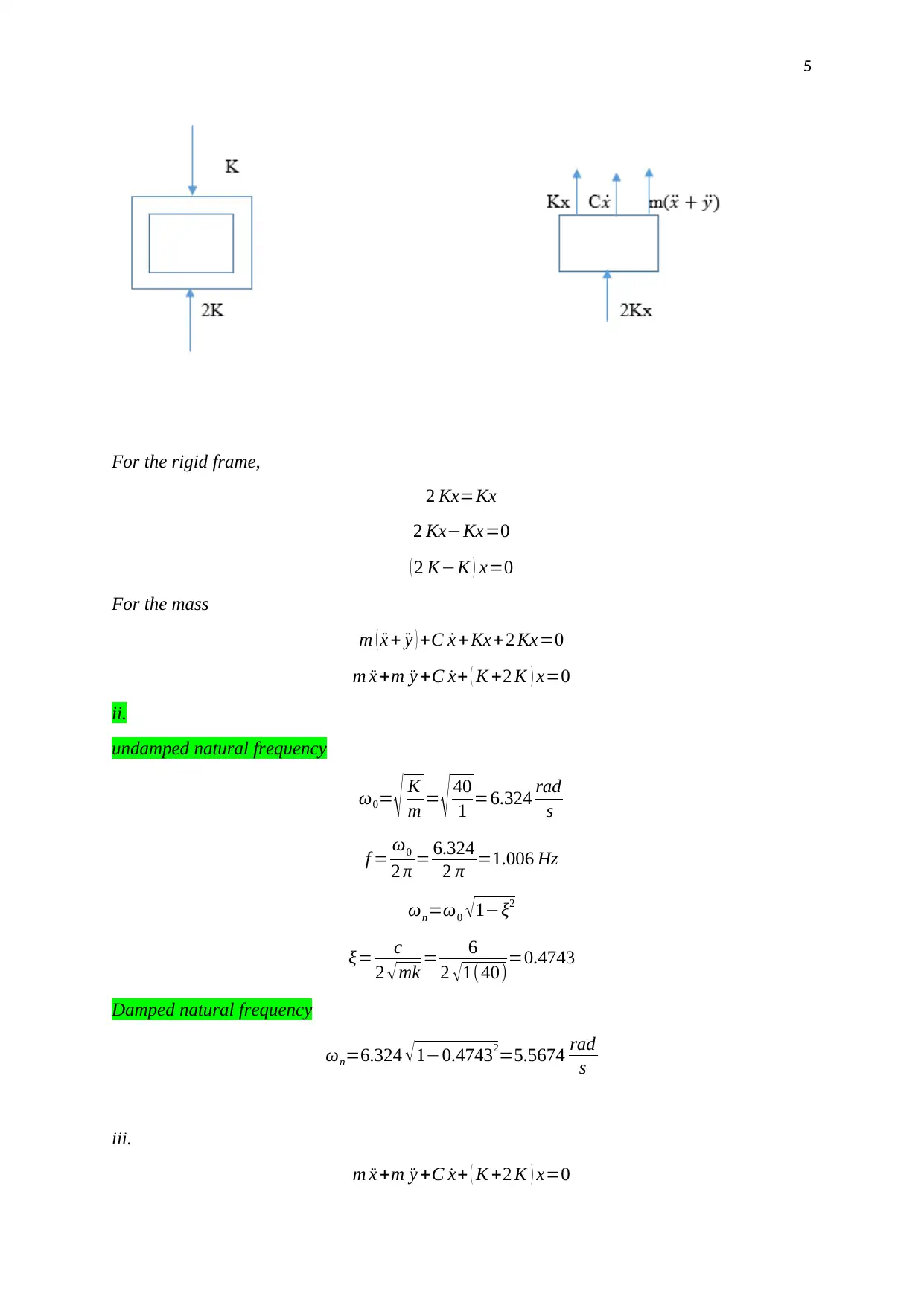
For the rigid frame,
2 Kx=Kx
2 Kx−Kx=0
( 2 K−K ) x=0
For the mass
m ( ¨x + ¨y ) +C ˙x +Kx+ 2 Kx=0
m ¨x +m ¨y +C ˙x+ ( K +2 K ) x=0
ii.
undamped natural frequency
ω0= √ K
m = √ 40
1 =6.324 rad
s
f = ω0
2 π = 6.324
2 π =1.006 Hz
ωn=ω0 √ 1−ξ2
ξ= c
2 √ mk = 6
2 √1(40)=0.4743
Damped natural frequency
ωn=6.324 √1−0.47432=5.5674 rad
s
iii.
m ¨x +m ¨y +C ˙x+ ( K +2 K ) x=0

6
Substituting the givem values we have,
¨x + ¨y +6 ˙x+ ( 40+80 ) x=0
¨x + ¨y +6 ˙x+120 x=0
¨x +6 ˙x+120 x= ¨y
y (t )= y0 sin wf t
y (t )=0.02 sin15 t
˙y ( t ) =0.3 cos 15 t
¨y ( t ) =−4.5 sin 15 t
¨x (t ) +6 ˙x (t ) +120 x ( t )=−4.5 sin15 t 1
This has a particular solution of the form,
x p ( t ) = X1 sin 15 t+ X2 cos 15t
˙x p ( t ) =15 X1 cos 15 t −15 X2 sin 15t
¨x p ( t ) =−225 X1 sin 15 t−225 X1 cos 15 t
Substituting in equation 1,
¿−225 X1 sin 15 t−225 X1 cos 15 t+6 (X1 cos 15 t−X2 sin 15t )+ 120(X1 sin 15t +X2 cos 15 t)=−4.5 sin 15 t
Collecting like terms we have,
−225 X1 sin 15t−225 X1 cos 15 t +6 X1 cos 15 t−6 X2 sin15 t +120 X1 sin 15 t+120 X2 cos 15 t +4.5 sin 15 t=0
( −225 X 1−6 X2 +120 X1 +4.5 ) sin 15 t+ (−225 X1 +6 X1 +120 X2 ) cos 15 t=0
Solving for X1 and X2
(−225 X 1−6 X2 +120 X1 +4.5 ) =0
(−225 X 1+6 X1+120 X 2 ) =0
−219 X1 +120 X2=0
120 X2=219 X 1
X2 =1.825 X1
−225 X1−6 X2+ 120 X1+ 4.5=0
−105 X1−6 X2=−4.5
−105 X1−6 (1.825 X1)=−4.5
−105 X1−10.95 X1 =−4.5

7
−115.95 X1=−4.5
X1 =0.0388
X2 =1.825 X1= ( 1.825 ) ( 0.0388 )=0.07081
Therefore,
x p (t )= X1 sin 15 t+ X2 cos 15t
x p ( t ) =0.0388sin 15 t+ 0.07081cos 15t
iv.
¨x (t ) +6 ˙x (t ) +120 x ( t )=−4.5 sin15 t
Taking Laplace transforms on both sides of the equation we have,
s2 X ( s ) +6 sX ( s ) +120 X ( s ) = L { 4.5sin 15 t }
Laplace transform of sin ( at )= a
s2 +a2 , therefore,
L { 4.5 sin 15 t }=4.5 a
s2+a2 , a=15
¿ 4.5 15
s2 +152 = 67.5
s2 +225
s2 X ( s ) +6 sX ( s ) +120 X ( s )= 67.5
s2 +225 =Y ( s)
X ( s )
Y (s )= (s2+ 6 s +120)
67.5
s2+ 225
= ( s2 +6 s+120 ) (s2+ 225)
67.5

8
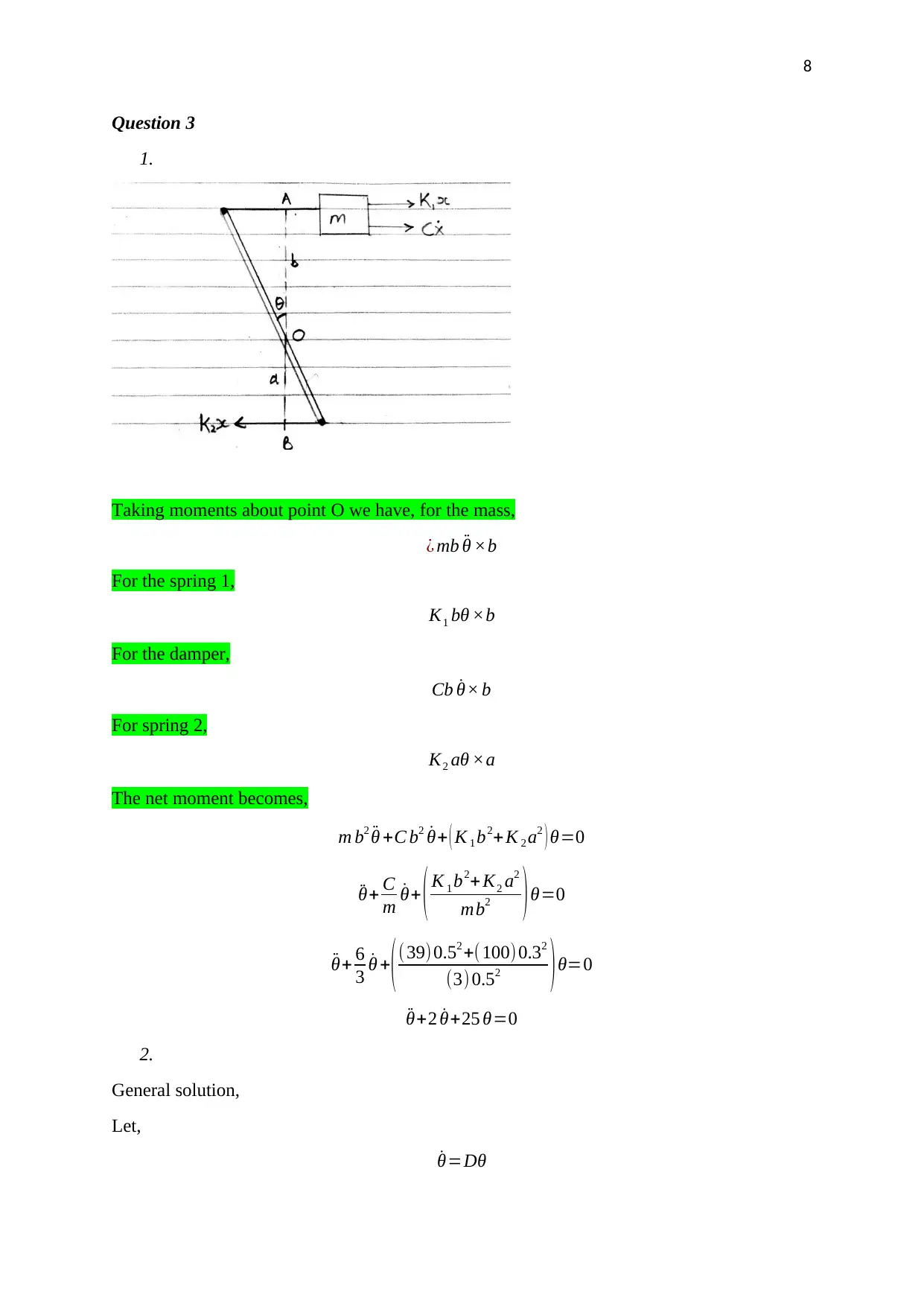
Question 3
1.
Taking moments about point O we have, for the mass,
¿ mb ¨θ ×b
For the spring 1,
K1 bθ ×b
For the damper,
Cb ˙θ× b
For spring 2,
K2 aθ ×a
The net moment becomes,
m b2 ¨θ +C b2 ˙θ+ ( K 1 b2+ K 2 a2 ) θ=0
¨θ+ C
m ˙θ+ ( K 1 b2+ K2 a2
mb2 ) θ=0
¨θ+ 6
3 ˙θ +
( (39) 0.52 +( 100)0.32
(3) 0.52 ) θ=0
¨θ+2 ˙θ+25 θ=0
2.
General solution,
Let,
˙θ=Dθ

9
¨θ=D2 θ
¨θ+2 ˙θ+25 θ=0
D2 θ+2 Dθ +25 θ=0
Solving for D we have,
D=−2 ± √4−100
2 =−2± √−96
2
D=−1± j √96
2
D=−1± 42 √ 6
2
D=−1± j 8 √ 6
The general solution becomes,
θg ( t ) =e−t [ Acos 8 √ 6 t+ Bsin8 √ 6 t ]
3.
Particular solution
F=10 δ (t−2)
D2 θ+2 Dθ +25 θ=F=10 δ(t−2)
[ D¿¿ 2+ 2 D+25 ]θ=F=10 δ (t−2) ¿
¿ 10 δ(t −2)
D2+2 D+25 = 10 δt
D2 +2 D+ 25 − 20 δ
D2 +2 D+25
¿ 10 δt
25 [1+ 2 D
25 + D2
25 ]− 20 δ
02+ 2(0)+25
X p =10 δ
25 [ 1+ 2 D
25 + D2
25 ]
−1
t− 20 δ
25
4.
The total solution then becomes,
Xtotal =e−t [ Acos 8 √ 6 t +Bsin 8 √ 6 t ] + 10 δ
25 [ 1+ 2 D
25 + D2
25 ]
−1
t− 20 δ
25

10
Question 4
F(t)
Kx m ¨x C ˙x
F ( t ) =m ¨x+C ˙x+Kx
Substituting the given coefficients we have,
F ( t ) = ¨x +12 ˙x +144 x
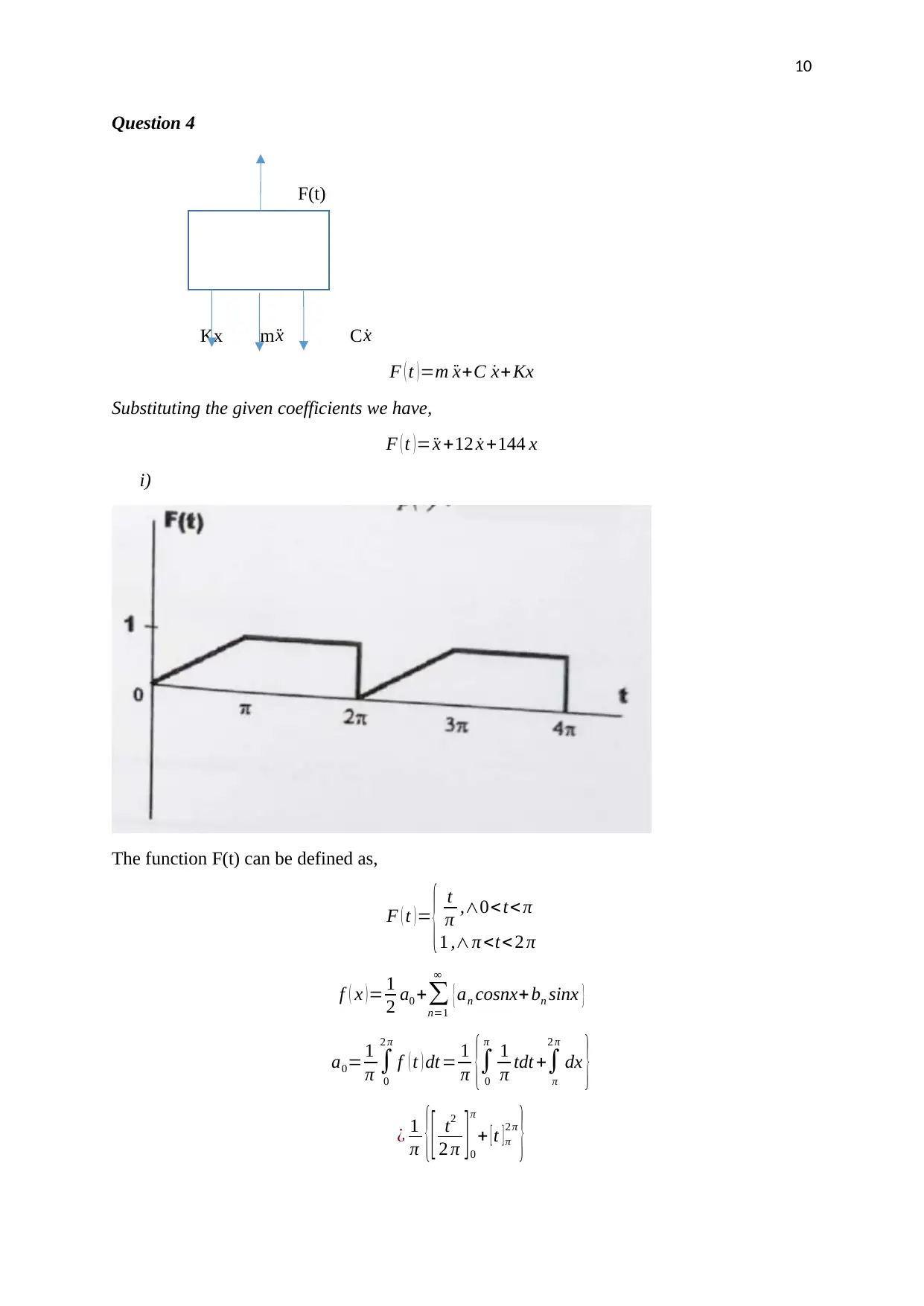
i)
The function F(t) can be defined as,
F ( t )= { t
π ,∧0< t< π
1 ,∧π <t< 2 π
f ( x )= 1
2 a0 +∑
n=1
∞
{an cosnx+ bn sinx }
a0= 1
π ∫
0
2 π
f ( t ) dt= 1
π {∫
0
π
1
π tdt +∫
π
2 π
dx }
¿ 1
π {[ t2
2 π ]0
π
+ [ t ] π
2 π
}

11
1
π { π
2 +2 π−π }= 1
π {3 π
2 }= 3
2
an= 1
π ∫
0
2 π
f ( t ) cosntdt = 1
π {∫
0
π
t
π cosntdt +∫
π
2 π
cosntdt }
¿ 1
π { 1
π [ tsinnt
n ]0
π
− 1
πn ∫
0
π
sinntdt+∫
π
2 π
cosntdt }
an= 1
π { 1
π ( 0−0 )− 1
πn [−cosnt
n ]0
π
+ [ sinnt
n ]π
2 π
}
1
π { −1
π n2 (− (−1 )n +1 )+(0−0) }
¿− 1
π2 n2 ¿
Therefore,
an=0( n even)
an= −2
π2 n2
Finding bn
bn= 1
π ∫
0
2 π
f ( t ) sinntdt = 1
π {∫
0
π
t
π sinntdt +∫
π
2 π
sinntdt }
¿ 1
π { 1
π [ −tcosnt
n ]0
π
+ 1
πn ∫
0
π
cosntdt +∫
π
2 π
sinntdt }
¿ 1
π { 1
πn (−πcosnπ ) + 1
πn [ sinnt
n ]0
π
+ [−cosnt
n ]π
2 π
}
¿ 1
π {−1
n cosnπ + ( 0−0 )− 1
n (cos 2 πn−cosπn)}
¿ 1
π {−1
n cosnπ + ( 0−0 )− 1
n (cos 2 πn−cosπn)}
¿ 1
π {−1
n cos 2 πn }=−1
πn cos 2 πn
But cos 2 πn=1
bn=−1
πn

12
f ( t )= 3
2 − 2
π 2 {cost+ 1
9 cos 3 t + 1
25 cos 5 t+… }− 1
π {sint + 1
2 sin 2 t+ 1
3 sin 3 t+ 1
4 sin 4 t … }
ii)
a0= 3
2
f ( t )= 3
2 − 2
π 2 cost− 1
π sint − 1
2 π sin 2 t
F ( t )= ¨x (t)+12 ˙x (t)+144 x (t) i
The particular solution can be written as,
x p ( t ) = X1 sint + X2 cost
˙x p ( t ) = X1 cost−X2 sint
¨x p ( t ) =−X1 sint− X1 cost
Substituting x p and its derivatives into equation i ,
(− X1 sint− X1 cost ) +12 ( X1 cost− X2 sint ) +144 ( X1 sint + X2 cost )= 3
2 − 2
π2 cost− 1
π sint
−X1 sint −X1 cost +12 X1 cost−12 X2 sint +144 X1 sint +144 X2 cost= 3
2 − 2
π2 cost− 1
π sint − 1
2 π sin 2 t
(− X1−12 X2+ 144 X1− 1
π ) sint + (−X 1+12 X1 ++144 X 2− 2
π2 ) cost= 3
2
The terms in parentheses must vanish which yields,
x p ( t ) =sint +cost −3
2
Question 5
1.