ENGIN2301 Mechanics of Solids Tutorial 1: Complete Solution

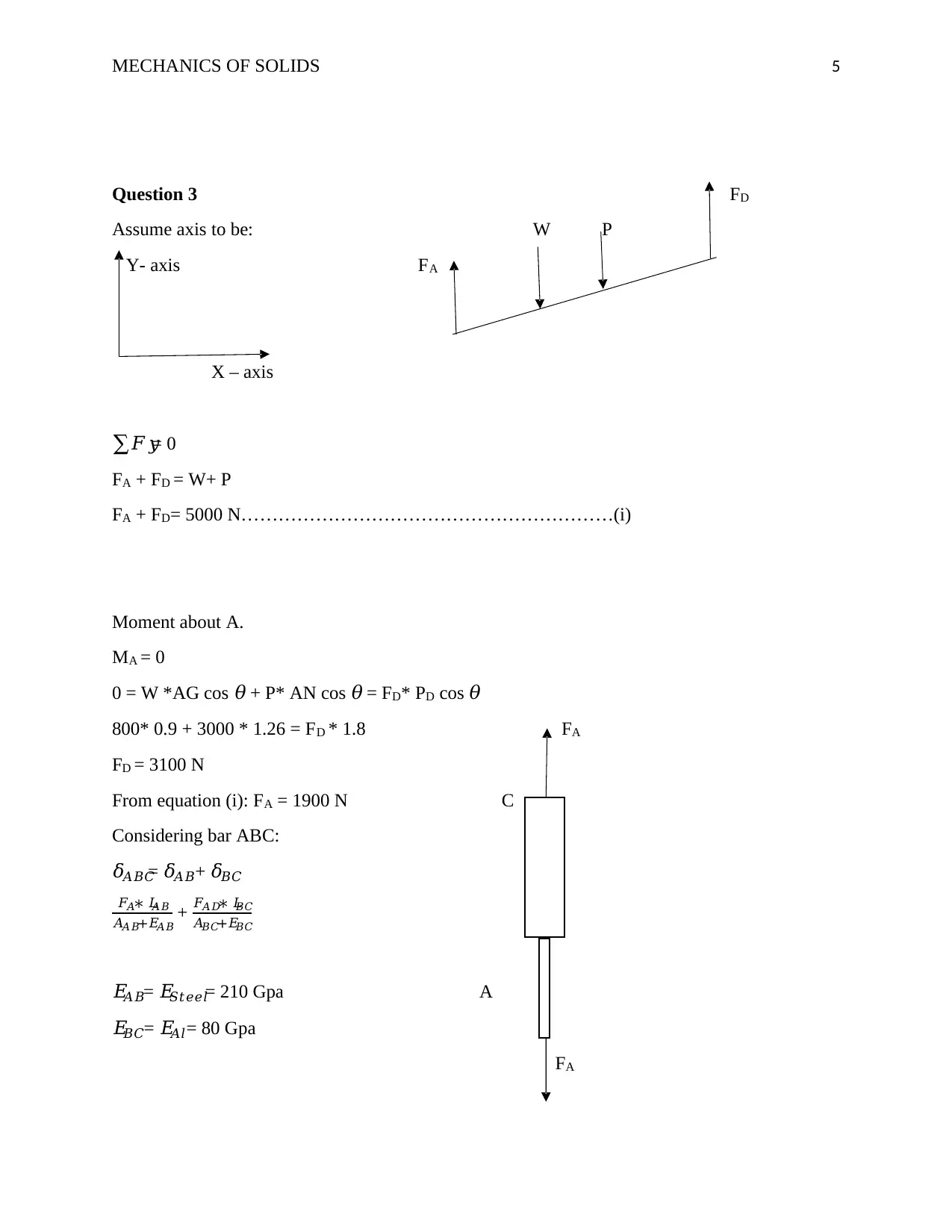
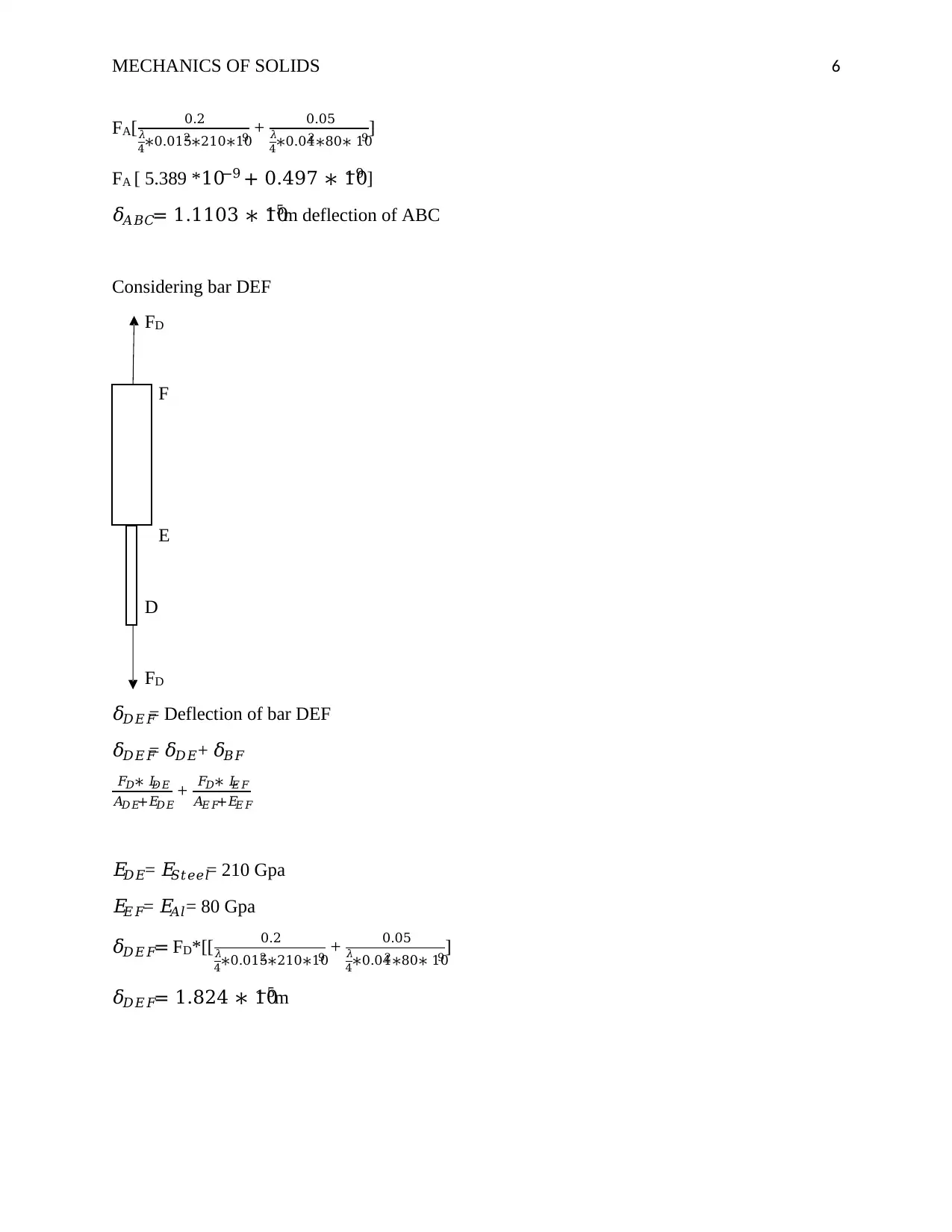
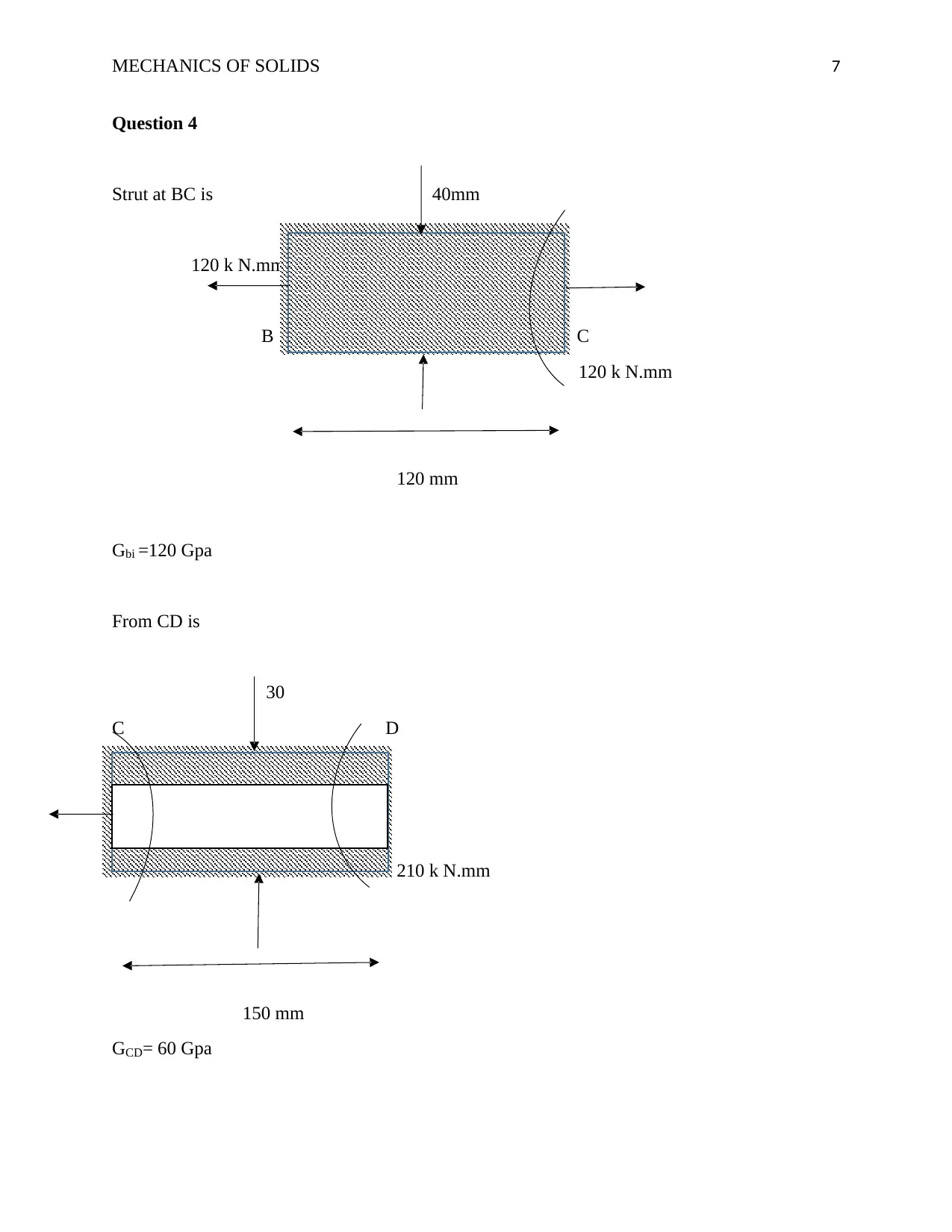
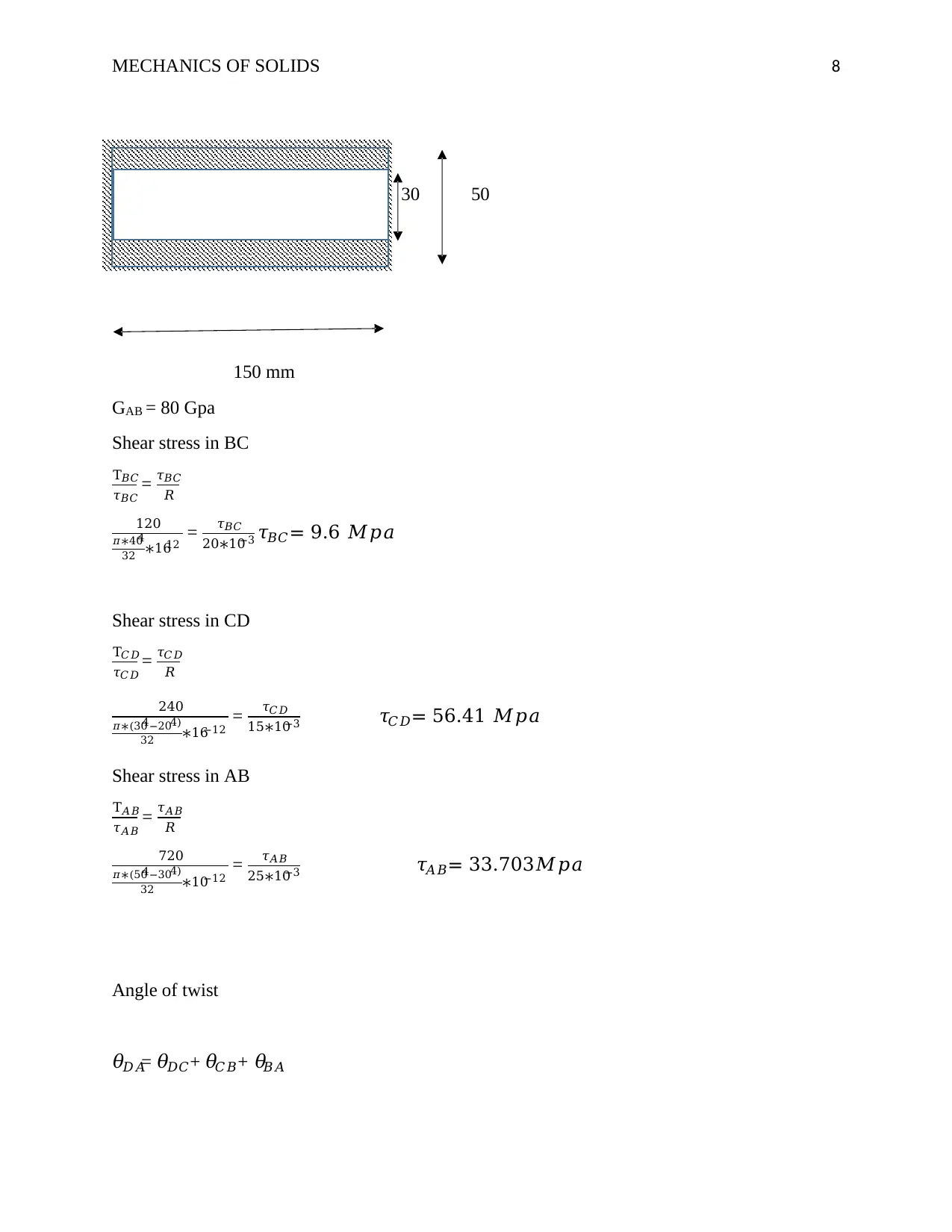
This document presents a comprehensive solution to a Mechanics of Solids tutorial assignment. The solution addresses two main questions involving structural analysis. Question 1 focuses on a platform supported by a cable and a strut, requiring the calculation of reaction forces, stress in the strut, shear stress in a bolt, and bearing stresses. This involves creating a free body diagram and applying equilibrium equations. Question 2 involves the analysis of a component supporting part of a machine. The solution includes calculations of resultant forces, shear stresses, and bearing stresses in various components. The document provides detailed step-by-step solutions, including calculations for stress, shear, bearing stress, and deflection, making it a valuable resource for students studying mechanics of solids. The assignment covers topics such as stress, shear, bearing stress, and deflection, including calculations for different components and scenarios.

Running Head: MECHANICS OF SOLIDS 1
MECHANICS OF SOLIDS
Student’s Name
Professor
Date

MECHANICS OF SOLIDS 2
Mechanics of Solids
Question 1
Free body diagram of figure 1.
RD
420 k N
300
RB RA
0.96 mm 0.09mm 1.05 mm
RD sin 30 – 420 + RB- RA………………………………………………. (i)
Moment at A.
RD sin 30(2.1) + RB (1.14)- 420(1.05)
2.1 RD sin 30 + 1.14(420+RA- RD sin 30) – 441= 0
2.1 RD sin 30 + 478.8 +1.14 RA- 1.14 RD sin 30-441=0
0.96 * 50 sin 30 + 37.8 +1.14 RA=0
RA = -54.21 k N
Substuting RA in equation (i)
2.1 RD sin 30 + 1.14 RB- 441= 0
RB= 420+RA -RD sin 30
RB= 340.8 k N

MECHANICS OF SOLIDS 3
Stress in the strut BC.
𝜕= 𝐹
𝐴 == 340.8
0.2
= 1703.95 N.mm
Shear stress on bolt at A.
𝜏 = 16𝑉
3𝜋𝑑2
𝜏 =16 ∗ −54.21
3𝜋(0.05)2
𝜏 = −36.807 𝑀𝑝𝑎
Bearing stresses on flange
3𝑉
2𝑏𝑑
3∗ −54.21
2∗0.15∗0.05 = -10.842 Mpa
Bearing stress on platform
3∗ −54.21
2∗0.2∗0.05
= -8.131 Mpa

MECHANICS OF SOLIDS 4
Question 2
Considering Static equilibrium
(∑M) A=0
(-Fy * 504.5) +(Fx *86.4) + Ry* (815.9 + 504.5) + (Rx *531.3)
=0
(-68*5530*504.5) +(68sin30 * 86.6) + Rcos 20(1320.6) + Rsin 20* 531.3=0
68[-393.709] + R [1422.485] =0
R= 68∗393.709
1422.985
R = 1822 k N
(∑Fy) =0
Ay – Fy + Ry = 0
Ay- 68cos 30 +18.82cos 20=0
Ay= 41.20 k N
(∑Fx) = 0
Ax – Fx + Rx = 0
Ax= 68sin 30-18.82sin 20
Ax= 27.56 k N
Resultant force at A.
FA= √((𝐴𝑥)2 + ((Ay)2) = √((27.56)2 + ((41.204)2)
FA = 49.57 k N
Both bolts are under single shear
𝜏A =
𝐹𝐴
(𝐴𝑟𝑒𝑎)𝐴
= 49.57∗103
(𝜋
4∗252)𝐴
= 100.99 Mpa
𝜏B =
𝑅
(𝐴𝑟𝑒𝑎)𝐵
= 18.82∗103
(𝜋
4∗202)𝐴
= 59.

MECHANICS OF SOLIDS 5
Question 3 FD
Assume axis to be: W P
Y- axis FA
X – axis
∑𝐹𝑦= 0
FA + FD = W+ P
FA + FD= 5000 N……………………………………………………(i)
Moment about A.
MA = 0
0 = W *AG cos 𝜃 + P* AN cos 𝜃 = FD* PD cos 𝜃
800* 0.9 + 3000 * 1.26 = FD * 1.8 FA
FD = 3100 N
From equation (i): FA = 1900 N C
Considering bar ABC:
𝛿𝐴𝐵𝐶= 𝛿𝐴𝐵+ 𝛿𝐵𝐶
𝐹𝐴∗ 𝐿𝐴𝐵
𝐴𝐴𝐵+𝐸𝐴𝐵
+ 𝐹𝐴𝐷∗ 𝐿𝐵𝐶
𝐴𝐵𝐶+𝐸𝐵𝐶
𝐸𝐴𝐵= 𝐸𝑆𝑡𝑒𝑒𝑙= 210 Gpa A
𝐸𝐵𝐶= 𝐸𝐴𝑙 = 80 Gpa
FA

MECHANICS OF SOLIDS 6
FA[ 0.2
𝜆
4∗0.0152∗210∗109 + 0.05
𝜆
4∗0.042∗80∗ 109]
FA [ 5.389 *10−9 + 0.497 ∗ 10−9 ]
𝛿𝐴𝐵𝐶= 1.1103 ∗ 10−5m deflection of ABC
Considering bar DEF
FD
F
E
D
FD
𝛿𝐷𝐸𝐹= Deflection of bar DEF
𝛿𝐷𝐸𝐹= 𝛿𝐷𝐸+ 𝛿𝐵𝐹
𝐹𝐷∗ 𝐿𝐷𝐸
𝐴𝐷𝐸+𝐸𝐷𝐸
+ 𝐹𝐷∗ 𝐿𝐸𝐹
𝐴𝐸𝐹+𝐸𝐸𝐹
𝐸𝐷𝐸= 𝐸𝑆𝑡𝑒𝑒𝑙= 210 Gpa
𝐸𝐸𝐹= 𝐸𝐴𝑙 = 80 Gpa
𝛿𝐷𝐸𝐹= FD*[[ 0.2
𝜆
4∗0.0152∗210∗109 + 0.05
𝜆
4∗0.042∗80∗ 109]
𝛿𝐷𝐸𝐹= 1.824 ∗ 10−5m

MECHANICS OF SOLIDS 7
Question 4
Strut at BC is 40mm
120 k N.mm
B C
120 k N.mm
120 mm
Gbi =120 Gpa
From CD is
30
C D
210 k N.mm
150 mm
GCD= 60 Gpa

MECHANICS OF SOLIDS 8
330 30 50
150 mm
GAB = 80 Gpa
Shear stress in BC
Τ𝐵𝐶
𝜏𝐵𝐶
= 𝜏𝐵𝐶
𝑅
120
𝜋∗404
32 ∗1612 = 𝜏𝐵𝐶
20∗10−3 𝜏𝐵𝐶= 9.6 𝑀𝑝𝑎
Shear stress in CD
Τ𝐶𝐷
𝜏𝐶𝐷
= 𝜏𝐶𝐷
𝑅
240
𝜋∗(304−204)
32 ∗16−12
= 𝜏𝐶𝐷
15∗10−3 𝜏𝐶𝐷= 56.41 𝑀𝑝𝑎
Shear stress in AB
Τ𝐴𝐵
𝜏𝐴𝐵
= 𝜏𝐴𝐵
𝑅
720
𝜋∗(504−304)
32 ∗10−12
= 𝜏𝐴𝐵
25∗10−3 𝜏𝐴𝐵= 33.703𝑀𝑝𝑎
Angle of twist
𝜃𝐷𝐴= 𝜃𝐷𝐶 + 𝜃𝐶𝐵 + 𝜃𝐵𝐴

MECHANICS OF SOLIDS 9
𝜃𝐷𝐴= Τ𝐶𝐷∗𝐿𝐶𝐷
𝐺𝐶𝐷∗𝜏𝐶𝐷
+ Τ𝐶𝐵∗𝑙𝐶𝐵
𝐺𝐶𝐵∗𝜏𝐶𝐵
+Τ𝐵𝐴∗𝐿𝐵𝐴
𝐺𝐴𝐵∗𝜏𝐴𝐵
𝜃𝐷𝐴= ( 240∗0.15
60∗ (304−204) + 120∗0.12
120∗404 + 720∗0.15
80∗(504−304)) 32
𝜋∗ 10−3
𝜃𝐷𝐴= 0.0124 𝜋𝑎𝑑
𝜃𝐷𝐴= 0.7 degrees