Analysis and Comparison of Merge Sort Algorithms (CM2100)
VerifiedAdded on 2023/06/10
|20
|3132
|309
Report
AI Summary
This report provides a detailed analysis and comparison of two implementations of the merge sort algorithm: recursive and iterative. The introduction provides background on sorting algorithms and the specific merge sort technique, highlighting its importance and applications. The experimental method section details the Java implementation, including the use of NetBeans IDE, and the generation of test cases for worst-case and average-case scenarios. The core of the report presents the algorithms, providing Java code for both iterative and recursive approaches. Experimental results are presented, including execution times and steps for both algorithms under worst-case and average-case conditions. The analysis section discusses time and space complexity, providing a theoretical understanding of the algorithm's efficiency. The conclusion summarizes the findings, comparing the performance of the two approaches and offering insights into their respective strengths and weaknesses. Appendices include the Java source code and graphical representations of the merge sort process.

Running head: MERGE SORT ALGORITHM ANALYSIS
Merge Sort Algorithm Analysis
Name of the student:
Name of the University:
Author note:
Merge Sort Algorithm Analysis
Name of the student:
Name of the University:
Author note:
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

1
MERGE SORT ALGORITHM ANALYSIS
Table of Contents
Introduction................................................................................................................................2
Experimental Method.................................................................................................................3
The Merge Sort algorithm......................................................................................................5
Iterative Algorithm.............................................................................................................5
Recursive algorithm...........................................................................................................5
Experimental Results.................................................................................................................6
Worst Case Scenario..............................................................................................................6
Recursive technique...........................................................................................................6
Iterative technique..............................................................................................................8
Average Case Scenario..........................................................................................................9
Recursive technique...........................................................................................................9
Iterative technique............................................................................................................10
Merge Sort Analysis.................................................................................................................11
Conclusion................................................................................................................................11
Appendices...............................................................................................................................13
Appendix 1...........................................................................................................................13
Appendix 2...........................................................................................................................16
Appendix 3...........................................................................................................................18
MERGE SORT ALGORITHM ANALYSIS
Table of Contents
Introduction................................................................................................................................2
Experimental Method.................................................................................................................3
The Merge Sort algorithm......................................................................................................5
Iterative Algorithm.............................................................................................................5
Recursive algorithm...........................................................................................................5
Experimental Results.................................................................................................................6
Worst Case Scenario..............................................................................................................6
Recursive technique...........................................................................................................6
Iterative technique..............................................................................................................8
Average Case Scenario..........................................................................................................9
Recursive technique...........................................................................................................9
Iterative technique............................................................................................................10
Merge Sort Analysis.................................................................................................................11
Conclusion................................................................................................................................11
Appendices...............................................................................................................................13
Appendix 1...........................................................................................................................13
Appendix 2...........................................................................................................................16
Appendix 3...........................................................................................................................18

2
MERGE SORT ALGORITHM ANALYSIS
MERGE SORT ALGORITHM ANALYSIS
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

3
MERGE SORT ALGORITHM ANALYSIS
Introduction
A sorting algorithm consists of a series of conditional and iterative instructions that
takes a list or array of elements as an input and then specified operations on them and finally
produces a sorted array. The sorting algorithms can be used with any types of data and sort
them according to the needs of ascending or descending order. The sorting techniques can be
further used in solving various programming problems. There are many sorting techniques
that are widely used all over by programmers to sort their sorting needs. These are mainly
listed as below:
Bubble sort
Selection sort
Insertion sort
Merge sort
Each of these sorting techniques has their own logic sequence and hence can be coded
with different algorithms. Therefore, the time complexities of each also varies.
Here in this report, the merge sort technique has been taken up for review and the two
types of merge sort algorithms which are the iterative merge sort technique and the recursive
merge sort technique. Furthermore, light will be thrown on both of these algorithms and
their time complexities are to be measured and analyzed to conclude about which among the
two techniques would be suitable. In order to complete this test, several data sets of different
data types are to be generated and then these data sets are to be sorted based on both the
algorithms. While generating the data sets, the best case, average case and the worst case
scenarios shall also be considered.
Furthermore, the results from the tests are to be critically analyzed with their relations
or differences to the theoretically expected performances. Graphs and result tables shall be
MERGE SORT ALGORITHM ANALYSIS
Introduction
A sorting algorithm consists of a series of conditional and iterative instructions that
takes a list or array of elements as an input and then specified operations on them and finally
produces a sorted array. The sorting algorithms can be used with any types of data and sort
them according to the needs of ascending or descending order. The sorting techniques can be
further used in solving various programming problems. There are many sorting techniques
that are widely used all over by programmers to sort their sorting needs. These are mainly
listed as below:
Bubble sort
Selection sort
Insertion sort
Merge sort
Each of these sorting techniques has their own logic sequence and hence can be coded
with different algorithms. Therefore, the time complexities of each also varies.
Here in this report, the merge sort technique has been taken up for review and the two
types of merge sort algorithms which are the iterative merge sort technique and the recursive
merge sort technique. Furthermore, light will be thrown on both of these algorithms and
their time complexities are to be measured and analyzed to conclude about which among the
two techniques would be suitable. In order to complete this test, several data sets of different
data types are to be generated and then these data sets are to be sorted based on both the
algorithms. While generating the data sets, the best case, average case and the worst case
scenarios shall also be considered.
Furthermore, the results from the tests are to be critically analyzed with their relations
or differences to the theoretically expected performances. Graphs and result tables shall be
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

4
MERGE SORT ALGORITHM ANALYSIS
presented according to the results of the analysis and a conclusion about the same is to be
reached.
Experimental Method
Before moving forward with the experiment, it is necessary to discuss the details of
the two algorithms that are in highlight in this report. The definitions and the process of the
two algorithms shall be clearly stated and then their source code shall be presented. This
source code of the algorithm will be written using the Java language, compiled and executed
in the NetBeans IDE. Furthermore, the inputs and outputs of the programs will be separately
tested for a set of basic data to examine the righteousness of the code. The time and space
complexities of the algorithms will be determined and presented for analysis.
In order to assist in the process of the analysis of the two algorithms, narrow
amendments in the code has been made that will allow the system to record the time of
execution for each process and also display the intermediate steps that the program goes
through. This will help the analysis in many a ways. Firstly, through the execution time
stamp, the time complexity of the programs can be portrayed and contrasted against each
other. Secondly, the intermediate steps will allow to view the inner breakdown steps that
differentiates the two algorithms and hence would allow the analysis process to conclude the
better suiting one from the two. The test cases that will be used for both the worst and the
average case scenarios.
The test case data sets were generated using an external method that is automatically
operated based on the user’s input. This input method takes in n number of elements into an
array which is either manually entered or generated using a random number generator or
sequence generator program. The average case scenario is to be tested using a general set of
data, where the size of the test cases or the array size will be pre-determined and the values
MERGE SORT ALGORITHM ANALYSIS
presented according to the results of the analysis and a conclusion about the same is to be
reached.
Experimental Method
Before moving forward with the experiment, it is necessary to discuss the details of
the two algorithms that are in highlight in this report. The definitions and the process of the
two algorithms shall be clearly stated and then their source code shall be presented. This
source code of the algorithm will be written using the Java language, compiled and executed
in the NetBeans IDE. Furthermore, the inputs and outputs of the programs will be separately
tested for a set of basic data to examine the righteousness of the code. The time and space
complexities of the algorithms will be determined and presented for analysis.
In order to assist in the process of the analysis of the two algorithms, narrow
amendments in the code has been made that will allow the system to record the time of
execution for each process and also display the intermediate steps that the program goes
through. This will help the analysis in many a ways. Firstly, through the execution time
stamp, the time complexity of the programs can be portrayed and contrasted against each
other. Secondly, the intermediate steps will allow to view the inner breakdown steps that
differentiates the two algorithms and hence would allow the analysis process to conclude the
better suiting one from the two. The test cases that will be used for both the worst and the
average case scenarios.
The test case data sets were generated using an external method that is automatically
operated based on the user’s input. This input method takes in n number of elements into an
array which is either manually entered or generated using a random number generator or
sequence generator program. The average case scenario is to be tested using a general set of
data, where the size of the test cases or the array size will be pre-determined and the values

5
MERGE SORT ALGORITHM ANALYSIS
will be entered at compile time, which will be in descending order. Secondly for the worst
case, the data for the array will be created using the in-built methods which will be designed
in such a way that the data in the array will be in a special way to generate the worst case. In
order to generate the worst case of merge sort, the merge operation that resulted in above
sorted array should result in maximum comparisons. The left and right sub-arrays involved in
the merge sort operation should store alternate elements of a sorted array for example {10,
20, 30, 40, 50, 60, 70, 80}. Therefore, the left sub-array should be {10, 30, 50, 70} and the
right sub-array should be {20, 40, 60, 80}. Now every element of the array will be compared
at-least once and that will result in maximum comparisons. We apply the same logic for left
and right sub-array as well. For array {10, 30, 50, 70}, the worst case will be when its left
and right sub-array are {10, 50} and {30, 70} respectively and for array {20, 40, 60, 80} the
worst case will occur for {20, 40} and {60,80}. This data set will be consisting of a large
number of elements to test the algorithm at the array’s utmost state. A modified code snippet
will be used in generating the worst case array whose main operational method is as follows.
private static void generateWorstCase(int a[], int l, int r)
{
if (l < r)
{
int m = l + (r - l) / 2;
int[] left = new int[m - l + 1];
int[] right = new int[r - m];
split(a, left, right, l, m, r);
generateWorstCase(left, l, m);
generateWorstCase(right, m + 1, r);
join(a, left, right, l, m, r);
}
}
MERGE SORT ALGORITHM ANALYSIS
will be entered at compile time, which will be in descending order. Secondly for the worst
case, the data for the array will be created using the in-built methods which will be designed
in such a way that the data in the array will be in a special way to generate the worst case. In
order to generate the worst case of merge sort, the merge operation that resulted in above
sorted array should result in maximum comparisons. The left and right sub-arrays involved in
the merge sort operation should store alternate elements of a sorted array for example {10,
20, 30, 40, 50, 60, 70, 80}. Therefore, the left sub-array should be {10, 30, 50, 70} and the
right sub-array should be {20, 40, 60, 80}. Now every element of the array will be compared
at-least once and that will result in maximum comparisons. We apply the same logic for left
and right sub-array as well. For array {10, 30, 50, 70}, the worst case will be when its left
and right sub-array are {10, 50} and {30, 70} respectively and for array {20, 40, 60, 80} the
worst case will occur for {20, 40} and {60,80}. This data set will be consisting of a large
number of elements to test the algorithm at the array’s utmost state. A modified code snippet
will be used in generating the worst case array whose main operational method is as follows.
private static void generateWorstCase(int a[], int l, int r)
{
if (l < r)
{
int m = l + (r - l) / 2;
int[] left = new int[m - l + 1];
int[] right = new int[r - m];
split(a, left, right, l, m, r);
generateWorstCase(left, l, m);
generateWorstCase(right, m + 1, r);
join(a, left, right, l, m, r);
}
}
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

6
MERGE SORT ALGORITHM ANALYSIS
The Merge Sort algorithm
Both the merge sort algorithms have been converted into JAVA program codes and
have been presented below with their optimal output screenshots and a simple input/output
analysis to figure out whether the desired output is obtained for a particular set of dummy
data or not. The graphical representation of a sample merge sort operation has been presented
in Appendix 3.
Iterative Algorithm
In this mechanism of merge sort, the complete array is treated as a collection of
several smaller arrays which are already sorted. Then, these smaller arrays are gradually
merged to form arrays of double their size. Every small array pieces are sorted individually at
each turn and are then merged back into the main array. Finally when all the smaller arrays
are sorted individually and merged as one, the array thus formed is seemed to have been
already sorted. All these breakdowns and merging is achieved through the use of iterative
FOR loop block statements. The merge sort algorithm using the iterative method has been
presented in Appendix 1. A simple test case has also been provided.
Recursive algorithm
The Recursive Merge Sort is also a Divide and Conquer algorithm, however unlike the
iterative method, this method uses the recursion technique in order to achieve the sorted
output. The recursive sort method divides the input array in two halves, then calls itself for
the two halves and keeps dividing until the arrays consist of single elements only. Then
merges the two sorted halves. The mergeSort() function is used for merging two halves. The
merge(a, l, m, r) is a key process that assumes that a[ left .... mid ] and a[ mid+1 .... right ]
are sorted and merges the two sorted sub-arrays into one unless the array of the original size
is obtained, which is then sorted. Both these merge sort algorithms produces the same output
MERGE SORT ALGORITHM ANALYSIS
The Merge Sort algorithm
Both the merge sort algorithms have been converted into JAVA program codes and
have been presented below with their optimal output screenshots and a simple input/output
analysis to figure out whether the desired output is obtained for a particular set of dummy
data or not. The graphical representation of a sample merge sort operation has been presented
in Appendix 3.
Iterative Algorithm
In this mechanism of merge sort, the complete array is treated as a collection of
several smaller arrays which are already sorted. Then, these smaller arrays are gradually
merged to form arrays of double their size. Every small array pieces are sorted individually at
each turn and are then merged back into the main array. Finally when all the smaller arrays
are sorted individually and merged as one, the array thus formed is seemed to have been
already sorted. All these breakdowns and merging is achieved through the use of iterative
FOR loop block statements. The merge sort algorithm using the iterative method has been
presented in Appendix 1. A simple test case has also been provided.
Recursive algorithm
The Recursive Merge Sort is also a Divide and Conquer algorithm, however unlike the
iterative method, this method uses the recursion technique in order to achieve the sorted
output. The recursive sort method divides the input array in two halves, then calls itself for
the two halves and keeps dividing until the arrays consist of single elements only. Then
merges the two sorted halves. The mergeSort() function is used for merging two halves. The
merge(a, l, m, r) is a key process that assumes that a[ left .... mid ] and a[ mid+1 .... right ]
are sorted and merges the two sorted sub-arrays into one unless the array of the original size
is obtained, which is then sorted. Both these merge sort algorithms produces the same output
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
7
MERGE SORT ALGORITHM ANALYSIS
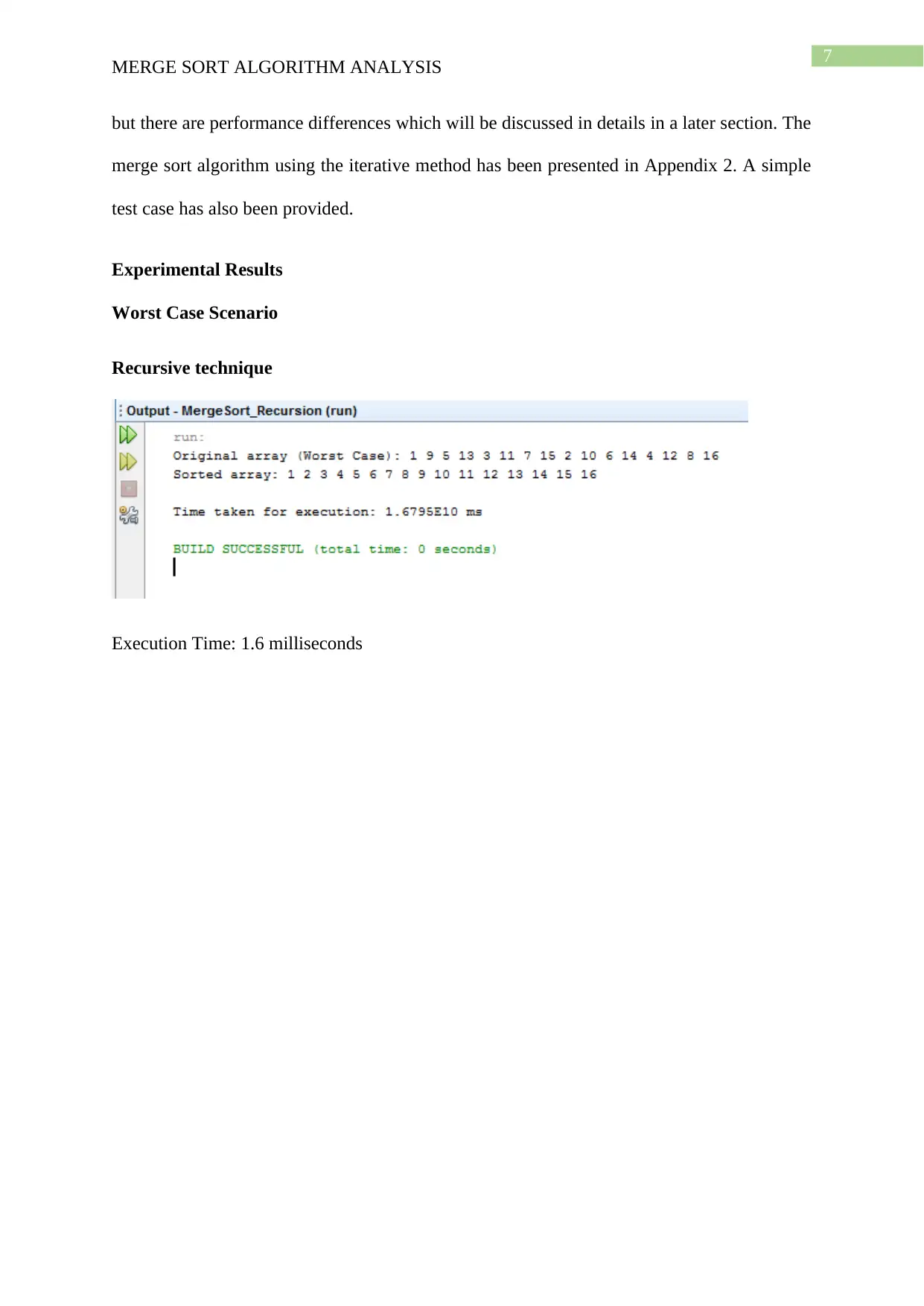
but there are performance differences which will be discussed in details in a later section. The
merge sort algorithm using the iterative method has been presented in Appendix 2. A simple
test case has also been provided.
Experimental Results
Worst Case Scenario
Recursive technique
Execution Time: 1.6 milliseconds
MERGE SORT ALGORITHM ANALYSIS
but there are performance differences which will be discussed in details in a later section. The
merge sort algorithm using the iterative method has been presented in Appendix 2. A simple
test case has also been provided.
Experimental Results
Worst Case Scenario
Recursive technique
Execution Time: 1.6 milliseconds
8
MERGE SORT ALGORITHM ANALYSIS
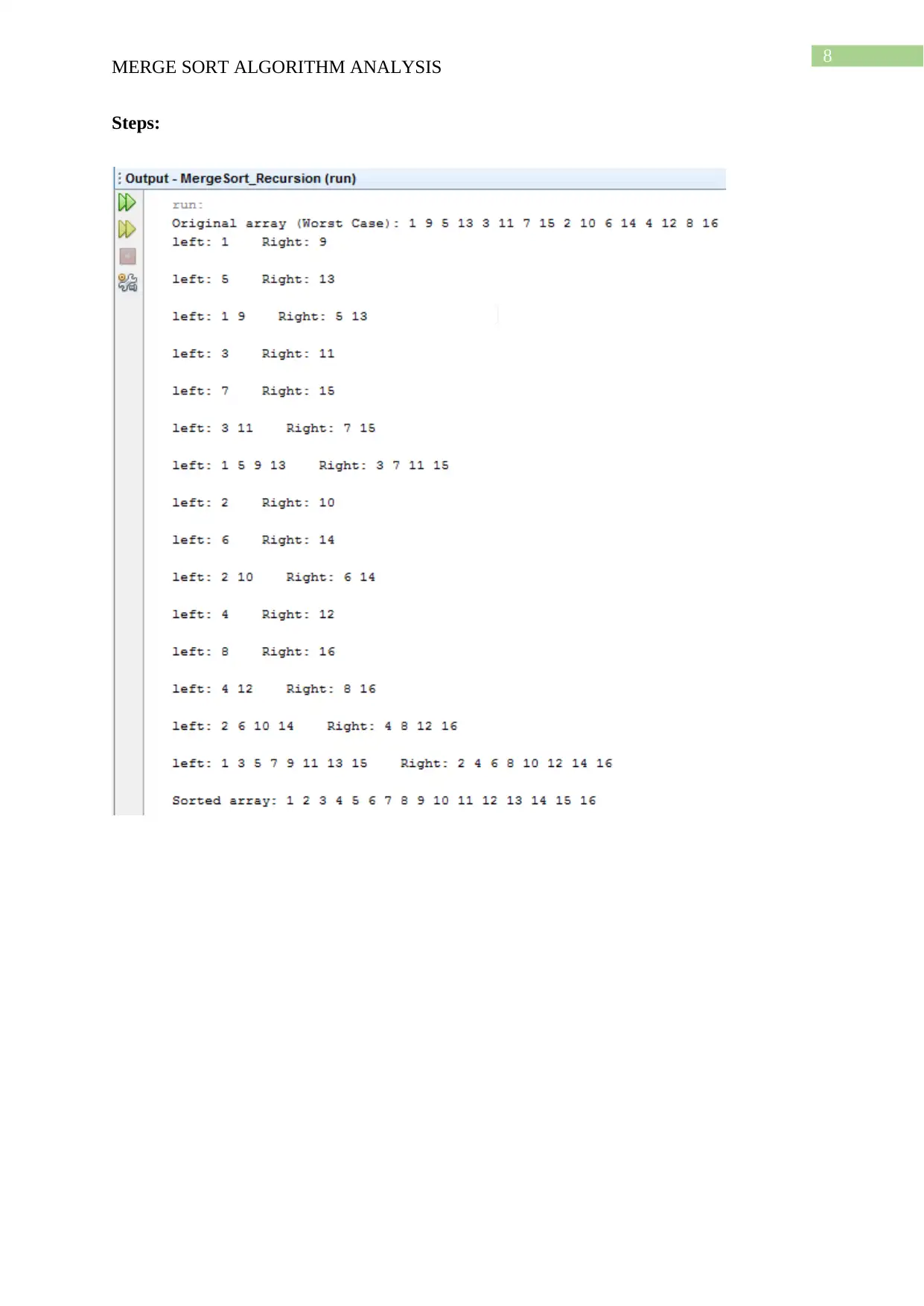
Steps:
MERGE SORT ALGORITHM ANALYSIS
Steps:
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
9
MERGE SORT ALGORITHM ANALYSIS
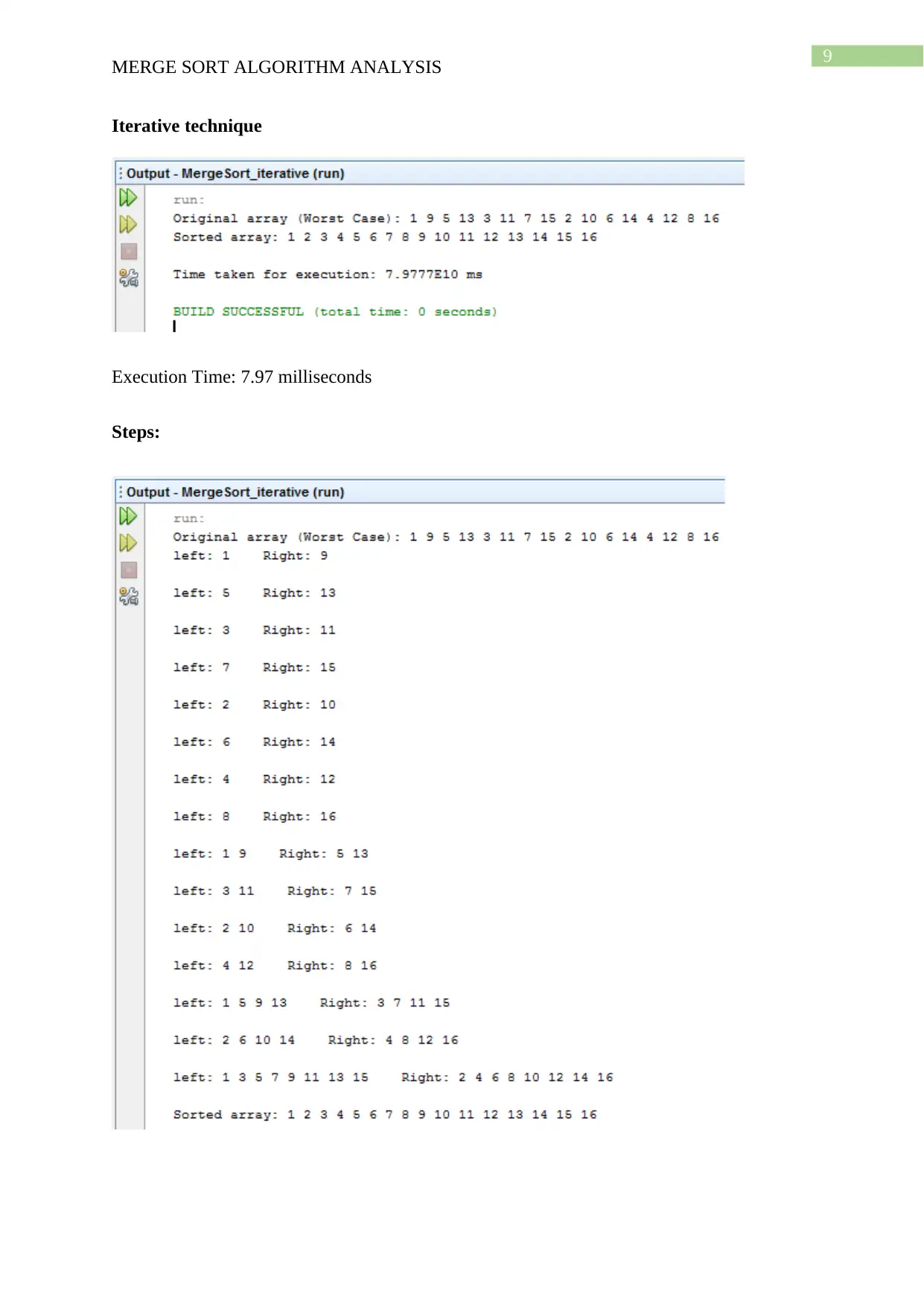
Iterative technique
Execution Time: 7.97 milliseconds
Steps:
MERGE SORT ALGORITHM ANALYSIS
Iterative technique
Execution Time: 7.97 milliseconds
Steps:
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
10
MERGE SORT ALGORITHM ANALYSIS
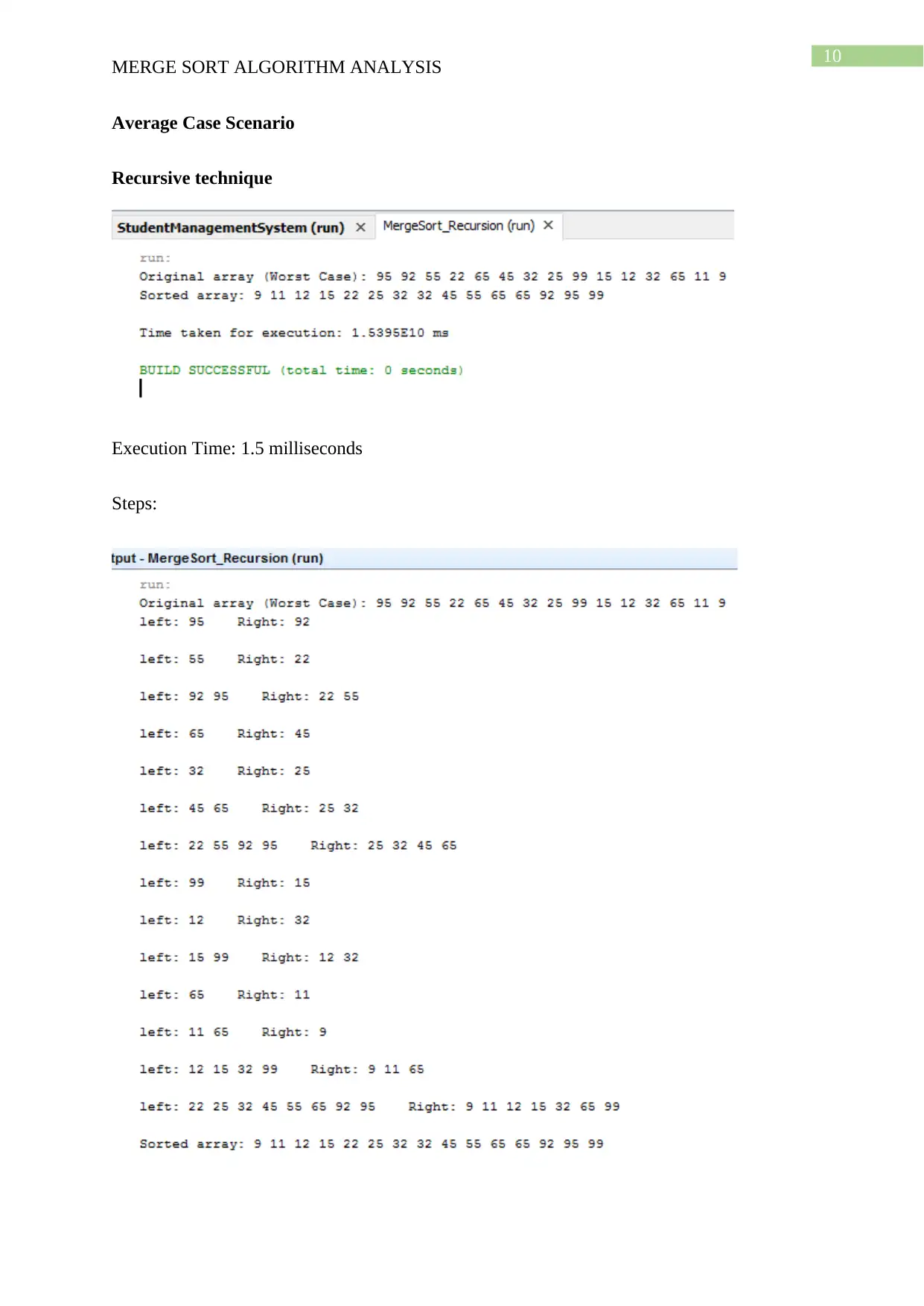
Average Case Scenario
Recursive technique
Execution Time: 1.5 milliseconds
Steps:
MERGE SORT ALGORITHM ANALYSIS
Average Case Scenario
Recursive technique
Execution Time: 1.5 milliseconds
Steps:
11
MERGE SORT ALGORITHM ANALYSIS
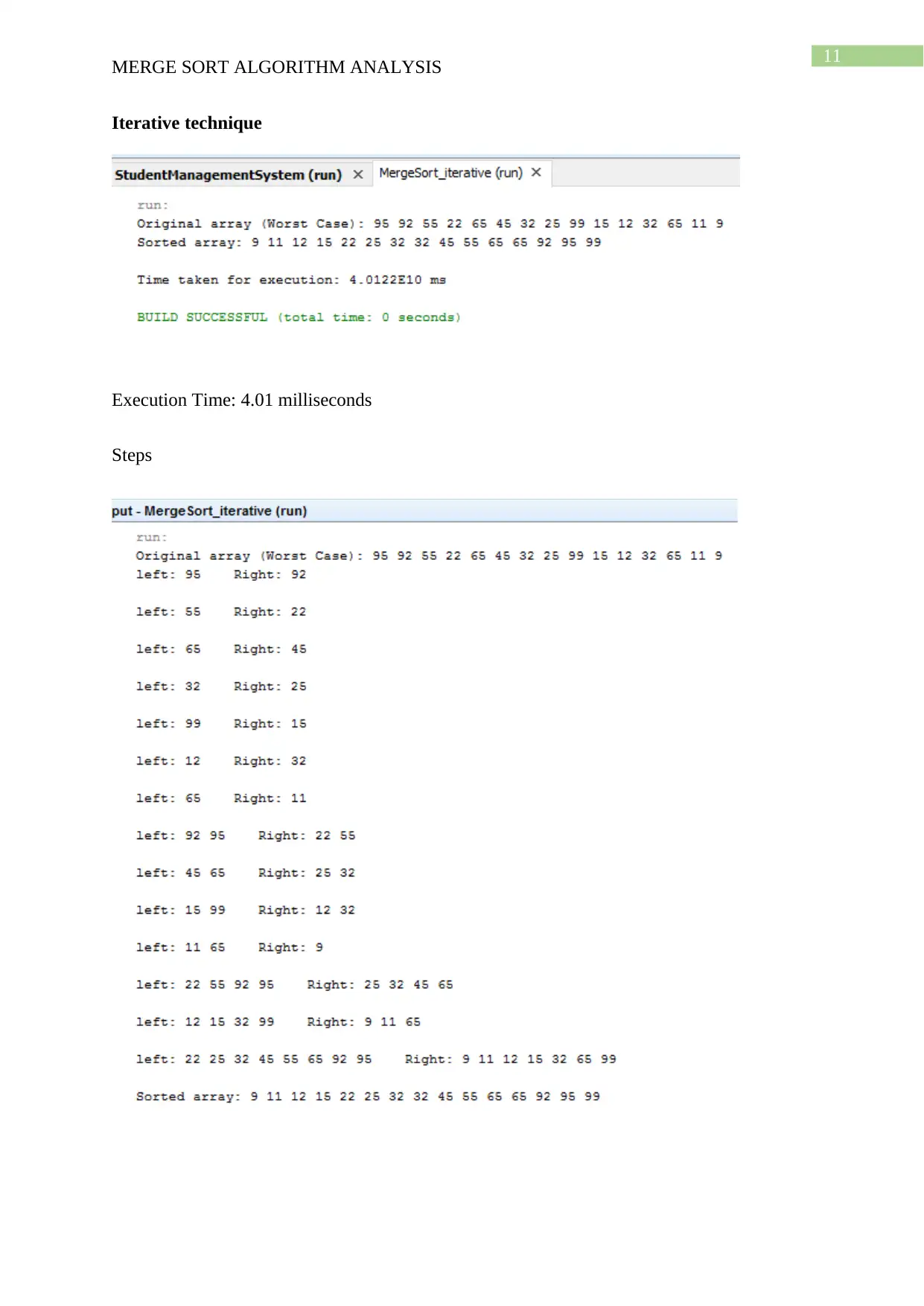
Iterative technique
Execution Time: 4.01 milliseconds
Steps
MERGE SORT ALGORITHM ANALYSIS
Iterative technique
Execution Time: 4.01 milliseconds
Steps
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 20
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.


