MHF4U - Unit 1 Assessment: Polynomials and Rational Functions

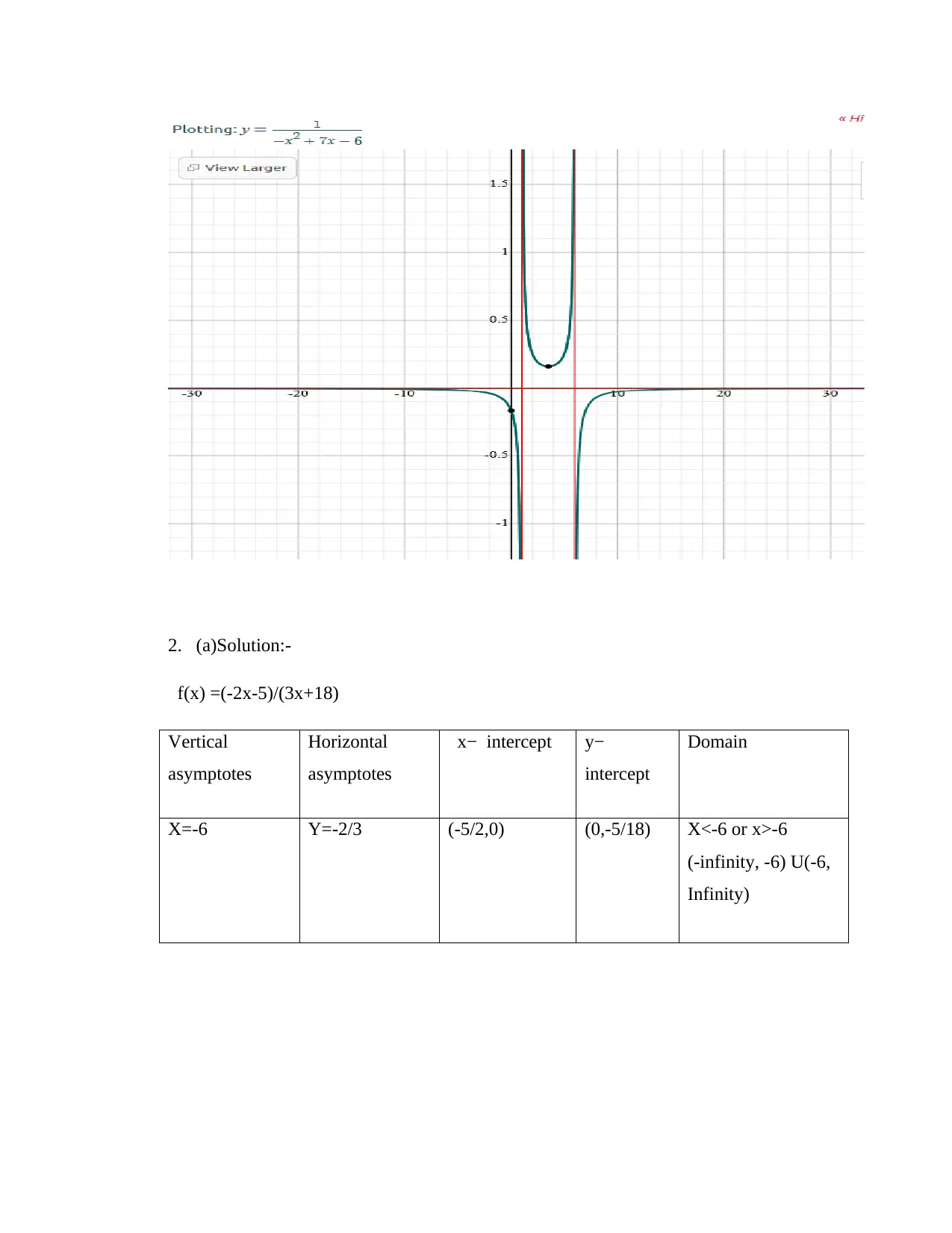
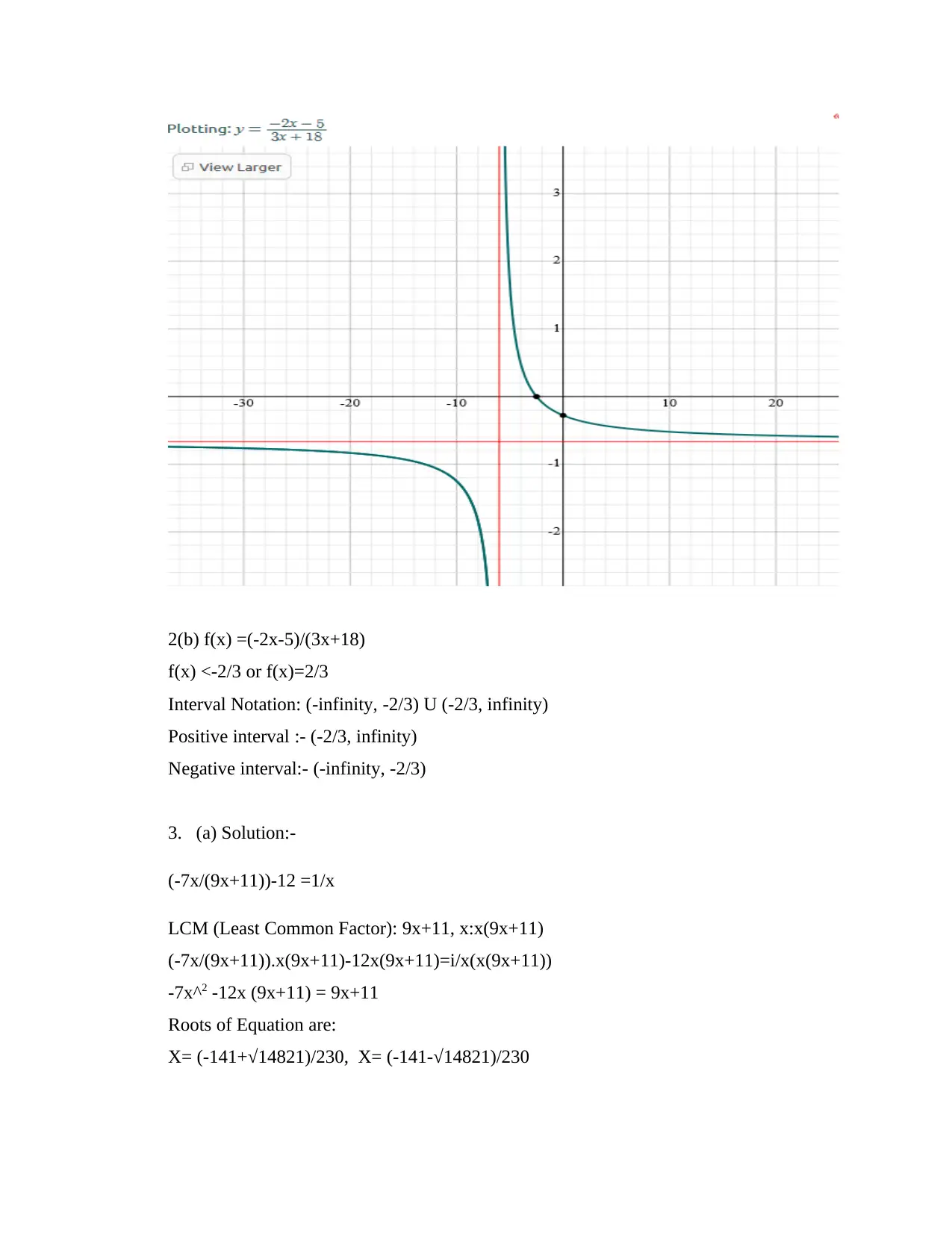
This document provides a comprehensive solution set for the MHF4U Unit 1 assessment, focusing on polynomials and rational functions. The solutions cover a range of topics, including identifying polynomial characteristics (degree, type, end behavior, domain), solving polynomial equations, sketching polynomial and rational function graphs, and determining intercepts and asymptotes. Detailed, step-by-step solutions are provided for each problem, including algebraic manipulations, transformations, and interpretations of graphical representations. The assessment also addresses rational equations, inequalities, and applications of polynomial functions to real-world problems, such as calculating volumes and dimensions. Overall, the solutions offer a valuable resource for students studying advanced functions, providing a clear understanding of the concepts and methods required to solve complex mathematical problems.

Unit 1 Assessment, Part 1
1.(a)Solution:-f (x) = − 1 /4 x 3 −13 x2 +3x −9
Degree Type of
polynomial
Sign of leading
coefficient
End behaviors Domain
3 Cubic 2 Infinity − 1 /4 x 3 −13 x2
+3x −9
Solution:--
Infinity<x< Infinity
Interval notation :
(-Infinity, Infinity)
1. Degree:- Maximum power of variable x.
2. Types of polynomial:- Depend upon the degree of the polynomial.
If degree= 1 then polynomial is Monomial
If degree= 2 then polynomial is Binomial
If degree= 3 then polynomial is cubic
3. Sign of Level :- No. of sign changes in the equation.
No. of sign changes with different sign from positive to negative.
No. of sign changes = Sign of leading coefficient
4. End Behavior:- That shows the polynomial x- axis goes to end value.
5. Domain:- Range of the polynomial lies is called domain of the polynomial.

1.(b) Solution:-
f (x) = 6x 4 + 7x 2 −8x+9
Degree Type of polynomial Sign of leading
coefficient
End behaviors Domain
4 Quartic 2 Infinity 6x 4 + 7x 2 −8x+9
Solution:-Infinity<x<
Infinity
Interval notation :
(-Infinity, Infinity)
2. Solution :-
f (x) =− ( x−4 ) (x+1) 2 ( x−5 )
x – intercepts and behavior
of graph at each x
intercepts
y − intercept End behaviors
x – intercepts Points:
(4,0),(-1,0),(5,0)
Behavior = Upto Infinity
(0,-20) Infinity

Plotting :-f (x) =−( x−4 ) (x+1) 2 ( x−5 )
3. Solution:-
Equation:-
0 =18 x 4 +87 x 3 +3 x2 −108x
3x(x-1)(3x+4)(2x+9)
3x(x-1)(3x+4)(2x+9)=0
Solve according to zero factor

Case1: X-1 =0
X=1
Case2: 3x+4=0
X= -4/3
Case3: 2x+9=0
X=-9/2
Factors are x=0, 1, -4/3, -9/2
Plotting:-

4(a) Solution:-
f (x) = [ 1/ 2 (x−5) ]3 −45
By using the formula
(a-b)^3 = a^3-3a^2b + 3ab^2-b^3
7{1/2(x^3-15x^2+75x-125)}-45
7{1/2(x^3-15x^2+75x-125)}=45
7{1 (x^3-15x^2+75x-125)} /2=45
7{1 (x^3-15x^2+75x-125)} =90
7x^3-105x^2+525x-875=90
7x^3-105x^2+525x+965
X intercepts (-1.405790)
Y intercepts (0,965)
Saddle point (5,1840)
Plotting:-
4(b) Solution:-
point (-9, -2446)
f (x) = [ 1/ 2 (x−5) ] 3 −45
On solving with this points we obtained

7x^3-105x^2+525x+965
Y=-2446
7x^3-105x^2+525x+965
X=-0.0603
5. Solution:-
function f (x) =mx4 +nx3 +68 x2 −x−6
Factors : (2x+1) and ( 4x−1 )
Case1: (2x+1) = 0
2x= -1
x=-1/2
Case2: (4x−1 ) = 0
x=-1/4
On putting the value x=-1/2 and x=-1/4 in equation mx4 +nx3 +68 x2 −x−6
We obtain
Put x=-1/2
m (-1/2)4 +n(-1/2)3 +68(-1/2)2-1/2-6
m (1/16)+n(-1/8)+17-1/2-6
m (1/16)+n(-1/8)+(34-1-12)/2
m/16 -n/8 +21/2
m- 2n +168…………………….(1)
Now put
x=-1/4
m (-1/4)4 +n(-1/4)3 +68(-1/4)2-1/2-6
m (1/256)+n(-1/64)+17/2-1/4-6
m/256- n/64 +9/4
m- 4n +576…………………(2)
On solving equation 1 and 2
m=168
n=168

6(a) Solution:-
f(x) =55 x 4 − x 2 −78
Function is odd when f(-x)= -f(x)
Function is even when f(-x)= f(x)
X intercept (√6/5 ,0) (-√6/5 ,0)
y intercept (0,-78)
For even or odd
f(x) =55 x 4 − x 2 −78
put x=-x
f(x) =55 (-1) 4 – (-1)2 −78
No change
f(-x)= f(x)
Graph is symmetrical.
Therefore function is even.

6(b) Solution:-
f(x) =37x3+93x
X intercept (0,0)
y intercept (0,0)
for even or odd
Function is odd when f(-x)= -f(x)
Function is even when f(-x)= f(x)
Put x=-x in equation
F(x)= 37x3+93x
F(-x)= 37(-1)3+93(-1)
Function is odd.
f(-x)= -f(x)
Mirror image of function in negative axis.

Unit 1 Assessment, Part 2
1. Solution:-
f(x) = − x 2 + 7x – 6
X- intercept (1,0)
Y –intercept (6,0)
Maximum at (7/2,25/4)
Graph:-
Reciprocal:-
f(x) = 1(− x 2 + 7x – 6)
Axis intercept point 1(− x 2 + 7x – 6) y(0,-1/6)
Extreme point Minimum (7/20,4/25)
f(x) = 1(− x 2 + 7x – 6)

2. (a)Solution:-
f(x) =(-2x-5)/(3x+18)
Vertical
asymptotes
Horizontal
asymptotes
x− intercept y−
intercept
Domain
X=-6 Y=-2/3 (-5/2,0) (0,-5/18) X<-6 or x>-6
(-infinity, -6) U(-6,
Infinity)

2(b) f(x) =(-2x-5)/(3x+18)
f(x) <-2/3 or f(x)=2/3
Interval Notation: (-infinity, -2/3) U (-2/3, infinity)
Positive interval :- (-2/3, infinity)
Negative interval:- (-infinity, -2/3)
3. (a) Solution:-
(-7x/(9x+11))-12 =1/x
LCM (Least Common Factor): 9x+11, x:x(9x+11)
(-7x/(9x+11)).x(9x+11)-12x(9x+11)=i/x(x(9x+11))
-7x^2 -12x (9x+11) = 9x+11
Roots of Equation are:
X= (-141+√14821)/230, X= (-141-√14821)/230