MITS5003 Wireless Networks & Communication: Term Paper Solution 2019S2

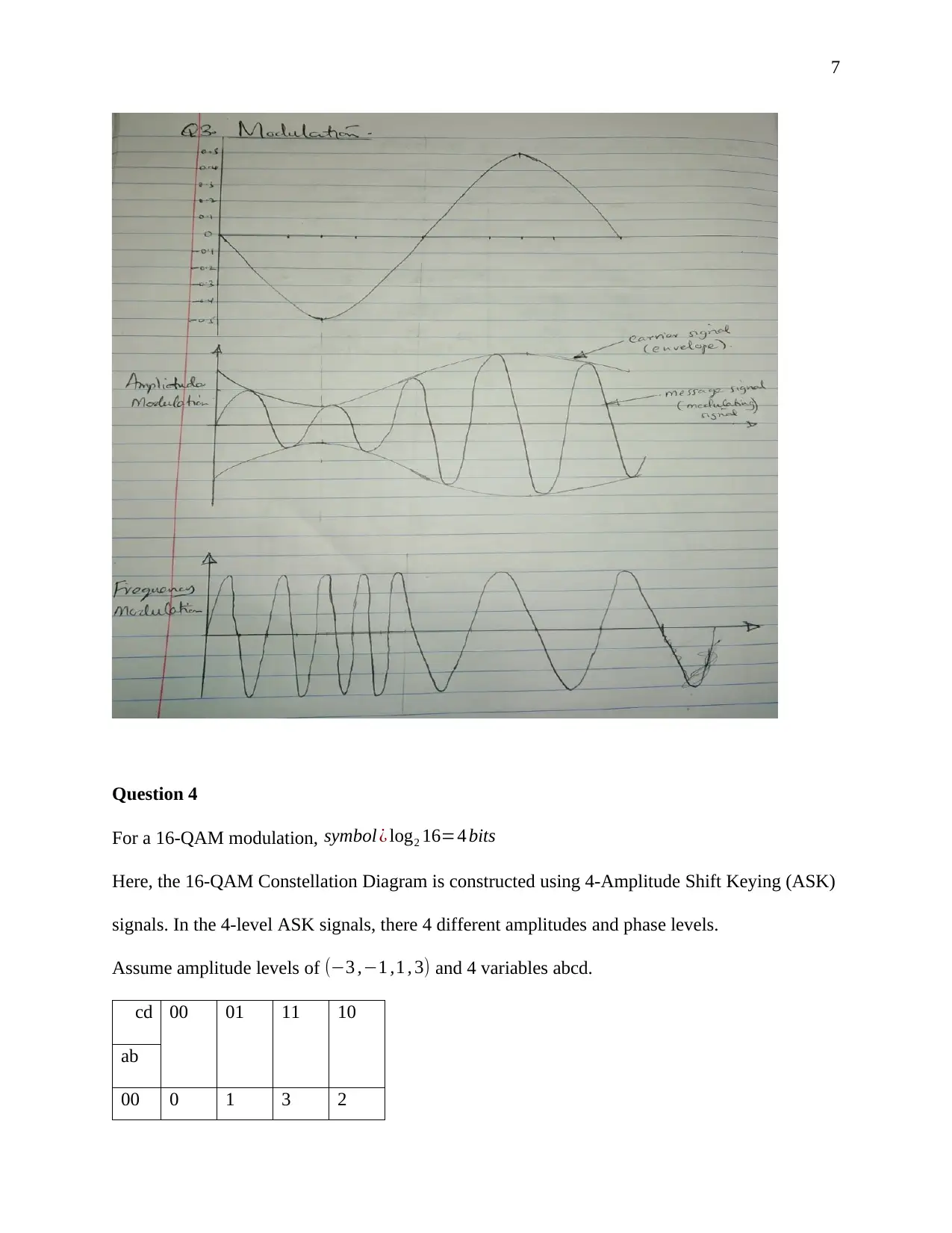
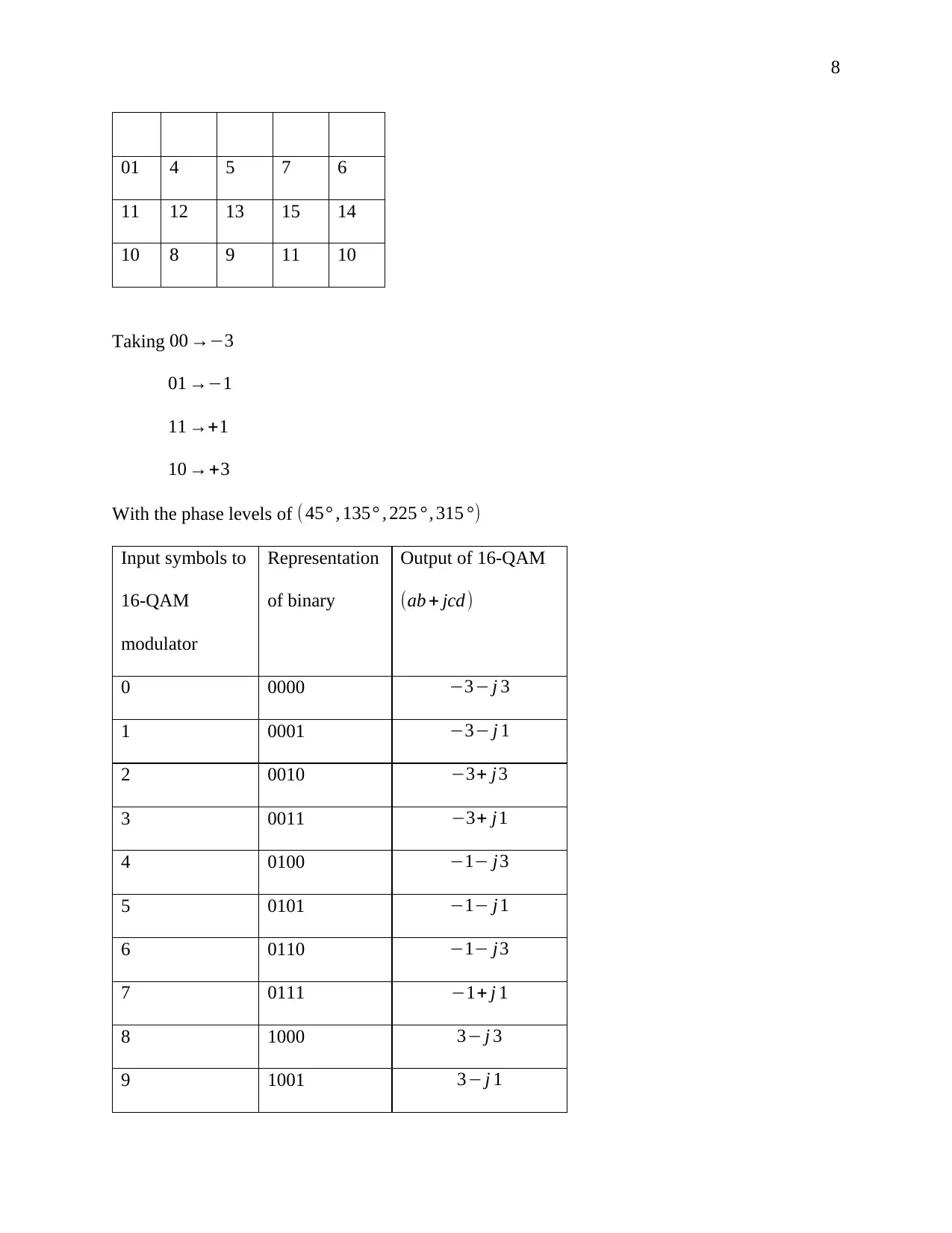
This document presents a comprehensive solution to a term paper assignment on wireless networks and communication. The assignment covers various topics, including the conversion of binary data to analog waveforms using different modulation techniques like ASK, FSK, PSK, and QAM. It includes calculations related to signal elements and frequencies. The solution also delves into Cyclic Redundancy Check (CRC) code generation and error detection, explaining the process with sender and receiver-end calculations and diagrams. Furthermore, the assignment addresses Direct Sequence Spread Spectrum (DSSS) and its application in wireless communication, including the use of XOR operations. Finally, the solution discusses the advantages of hexagonal cell structures in cellular networks, comparing them to square and circle-shaped cells in terms of coverage and performance. This assignment is designed to provide a complete understanding of key concepts in wireless communication and network design.

1
Wireless Networks and Communication
Term Paper
Date
840 words
Student Name
Institution Name

2
Question 1
Conversion of the binary data 110101 to analog waveforms using:
a) Two-level ASK
b) Two-level FSK
c) Two-level PSK

3
d) Differential PSK
e) Four-level ASK

4
f) Four-level PSK
g) Eight-level ASK

5
Question 2
From the questionf c=1000 kHz , f d=50 kHz , M =16( L=4 bits);
M =2L is the number of different signal elements where L is the bits per signal element.
From the formulaf i=f c+(2 i−1−M )f d, we compute the frequencies of the 16, 4-bit
combinations as follow:
f 1=1000+ ( 2 ×1−1−16 ) ×50=250 kHz
f 2=1000+ ( 2 ×2−1−16 ) ×50=350 kHz
f 3=1000+ ( 2 ×3−1−16 ) ×50=450 kHz
f 4=1000+ ( 2× 4−1−16 ) × 50=550 kHz
f 5=1000+ ( 2 ×5−1−16 ) ×50=650 kHz
f 6=1000+ ( 2 ×6−1−16 ) × 50=750 kHz
f 7=1000+ ( 2 ×7−1−16 ) × 50=850 kHz
f 8=1000+ ( 2 ×8−1−16 ) × 50=950 kHz

6
f 9=1000+ ( 2 ×9−1−16 ) × 50=1050 kHz
f 10=1000+ ( 2 ×10−1−16 ) ×50=1150 kHz
f 11=1000+ ( 2× 11−1−16 ) × 50=1250 kHz
f 12=1000+ ( 2× 12−1−16 ) × 50=1350 kHz
f 13=1000+ ( 2× 13−1−16 ) ×50=1450 kHz
f 14=1000+ ( 2 ×14−1−16 ) × 50=1550 kHz
f 15=1000+ ( 2× 15−1−16 ) ×50=1650 kHz
f 16=1000+ ( 2 ×16−1−16 ) ×50=1750 kHz
Question 3

7
Question 4
For a 16-QAM modulation, symbol ¿ log2 16=4 bits
Here, the 16-QAM Constellation Diagram is constructed using 4-Amplitude Shift Keying (ASK)
signals. In the 4-level ASK signals, there 4 different amplitudes and phase levels.
Assume amplitude levels of (−3 ,−1 ,1 , 3) and 4 variables abcd.
cd 00 01 11 10
ab
00 0 1 3 2

8
01 4 5 7 6
11 12 13 15 14
10 8 9 11 10
Taking 00 →−3
01 →−1
11 →+1
10 →+3
With the phase levels of (45° , 135° , 225 ° , 315 °)
Input symbols to
16-QAM
modulator
Representation
of binary
Output of 16-QAM
(ab + jcd)
0 0000 −3− j 3
1 0001 −3− j 1
2 0010 −3+ j 3
3 0011 −3+ j1
4 0100 −1− j3
5 0101 −1− j 1
6 0110 −1− j3
7 0111 −1+ j 1
8 1000 3− j 3
9 1001 3− j 1

9
10 1010 3+ j3
11 1011 3+ j1
12 1100 1− j3
13 1101 1− j1
14 1110 1+ j 3
15 1111 1+ j 1
Question 5
In the generation of the CRC code, the generator polynomial say G(x) must be agreed upon by
the sender and the receiver beforehand. Bit strings representation comes in terms of polynomials
with the coefficients as 0’s and 1’s.
CRC uses modulo-2 division i.e. the XOR operation.
The process of error detection in a CRC involves the following steps:

10
i. Sender end calculation of CRC code
ii. Appending CRC code to the initial data to be transmitted and sending
iii. The receiver end calculation of CRC code
iv. Checking for error
CRC diagram
Question 6
Given that, Message=111010110 , Pattern=101110 ,we can compute the Frame Check Sequence
(FCS) by use of CRC method as follows:
Number of bits in data set: n=9
Number of bits in pattern: k =6
FCS, k −1 bits=5 bits
Sender side

11
i. Binary data is augmented by k −1 zeros in end of data
ii. The message is divided by the pattern using modulo-2 division
iii. Append the remainder at end of data and send
Appending 5 zeros at the end: 11101011000000
Modulo-2 division at sender end:
We have to append the remainder i.e. 5 bits of FCS to the data at the receiver end
Sent message is: 11101011001100
Receiver side:
Message received: 11101011001100

12
Modulo-2 division (XOR operation) is performed at the receiver end and in the case of no
remainder, then no error exists.
In this particular case, we have all zeros as the remainder of the XOR operations hence there are
no errors in the received data.
Question 7
The given input=101
Locally generated PN bit stream: 011011010110
T =4 T c
In the Direct Sequence Spread Spectrum (DSSS) method, the transmitted signal is computed as
follows:
DSSS method is popularly used in wireless communication and it involves modulation and
transmission using the principle of intentionally spreading the narrow band signals over a larger