ELE2024 Group Coursework Solution: Modeling, Linearisation, Control
VerifiedAdded on 2022/08/27
|15
|1128
|14
Homework Assignment
AI Summary
This document provides a comprehensive solution to the ELE2024 group coursework, focusing on modeling, linearisation, transfer functions, PID controllers, and control system design. The solution covers three main problems: a dynamic model analysis, a ball and beam system analysis, and an inverted pendulum analysis. Part A addresses a dynamic model, analyzing its stability, step and impulse responses, and Bode plots. Part B focuses on the ball and beam system, deriving state-space representations, transfer functions, and root locus plots to determine system stability and controller requirements. Part C delves into the inverted pendulum, deriving transfer functions, analyzing stability using poles, and exploring controller design. The coursework also includes a team collaboration questionnaire, detailing the group's approach to problem-solving, software usage, and collaborative efforts. The solution utilizes MATLAB for simulations and analysis to verify the answers and provide a complete understanding of the concepts.

1. Part A
A1
Assuming zero initial conditions,
V (s )
I (s) =R+ Ls+ ( R+Ls ) 2 R
R +Ls+2 R
¿ R+ Ls+ ( R+ Ls ) 2 R
Ls +3 R
¿ RLs+ L2 s2 +3 R2+ 3 RLs+ 2 R2 +2 RL
Ls+ 3 R
¿ L2 s2 +6 RLs+5 R2
Ls +3 R
¿
s2+ 6 R
L s+5 ( R
L )2
s
L +3 R
L2
¿
s2+ 6 R
L s+5 ( R
L )2
1
L (s+ 3 R
L )
∴ I (s)
V (s) =
1
L ( s + 3 R
L )
s2 +6 R
L s +5 ( R
L )
2
The above relationship describes the dynamic model that describe the dynamic relationship between V ¿
and I
A2)
If the poles of the transfer function are in the left hand plane of the s-plane then the system should be
BIBO stable
From the characteristic equation describing the system, the poles are given by
s2 +6 R
L s+5 ( R
L )
2
=0
A1
Assuming zero initial conditions,
V (s )
I (s) =R+ Ls+ ( R+Ls ) 2 R
R +Ls+2 R
¿ R+ Ls+ ( R+ Ls ) 2 R
Ls +3 R
¿ RLs+ L2 s2 +3 R2+ 3 RLs+ 2 R2 +2 RL
Ls+ 3 R
¿ L2 s2 +6 RLs+5 R2
Ls +3 R
¿
s2+ 6 R
L s+5 ( R
L )2
s
L +3 R
L2
¿
s2+ 6 R
L s+5 ( R
L )2
1
L (s+ 3 R
L )
∴ I (s)
V (s) =
1
L ( s + 3 R
L )
s2 +6 R
L s +5 ( R
L )
2
The above relationship describes the dynamic model that describe the dynamic relationship between V ¿
and I
A2)
If the poles of the transfer function are in the left hand plane of the s-plane then the system should be
BIBO stable
From the characteristic equation describing the system, the poles are given by
s2 +6 R
L s+5 ( R
L )
2
=0
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

This implies poles=
−6 R
L ± √ ( 6 R
L )2
−20 ( R
L )2
2
poles=
−6 R
L ± √16 ( R
L )2
2
poles=
−6 R
L ± 4 R
L
2
∴ poles of the system are s1=−R
L ∧s2=−5 R
L
Since both the poles lie on the left hand side of the s-plane, then the system is BIBO stable. In other
words, for every bounded input to the system there will be a bounded output.
A3)
I step (t) is the step response for Vin input signal
I (s)
V (s )=
1
L (s + 3 R
L )
(s + R
L )(s+ 5 R
L )
⇒ I ( s )=
1
L (s+ 3 R
L )
(s+ R
L )(s+ 5 R
L ) ∙V ( s)
For a step voltage input V ( s )= 1
s ⇒ I ( s )=
1
L (s+ 3 R
L )
(s+ R
L )(s+ 5 R
L ) ∙ 1
s
−6 R
L ± √ ( 6 R
L )2
−20 ( R
L )2
2
poles=
−6 R
L ± √16 ( R
L )2
2
poles=
−6 R
L ± 4 R
L
2
∴ poles of the system are s1=−R
L ∧s2=−5 R
L
Since both the poles lie on the left hand side of the s-plane, then the system is BIBO stable. In other
words, for every bounded input to the system there will be a bounded output.
A3)
I step (t) is the step response for Vin input signal
I (s)
V (s )=
1
L (s + 3 R
L )
(s + R
L )(s+ 5 R
L )
⇒ I ( s )=
1
L (s+ 3 R
L )
(s+ R
L )(s+ 5 R
L ) ∙V ( s)
For a step voltage input V ( s )= 1
s ⇒ I ( s )=
1
L (s+ 3 R
L )
(s+ R
L )(s+ 5 R
L ) ∙ 1
s

⇒ I ( s ) = ( 3
5 R )
s + ( −1
2 R )
s+ R
L
+ ( −1
10 R )
s+5 R
L
I step (t) is the inverse Laplace transform of I (s )
⇒ I step (t )= 3
5 R u ( t )− 1
2 R e
−R
L t
u ( t )− 1
10 R e−5 R
L t
u ( t )
Final value means as t → ∞
I step ( t ) final= 3
5 R
Taking the gradient of I (t) w.r.t time
∂ I (t )
∂ x = −1
2 R ( −R
L ) e
−R
L t
− −1
10 R ( −5 R
L ) e
−5 R
L t
Initial value of gradient at t=0
∂ I (t )
∂ x = 1
L at t=0
A4)
I step ( t )= 3
5 R u ( t )− 1
2 R e
−R
L t
u ( t )− 1
10 R e−5 R
L t
u ( t )
Impulse response h ( t )= d
dt s (t) where s(t) is step response
⇒ 1
2 L e
−R
L t
u ( t ) + 1
2 L e−5 R
L t
u ( t )
A5)
5 R )
s + ( −1
2 R )
s+ R
L
+ ( −1
10 R )
s+5 R
L
I step (t) is the inverse Laplace transform of I (s )
⇒ I step (t )= 3
5 R u ( t )− 1
2 R e
−R
L t
u ( t )− 1
10 R e−5 R
L t
u ( t )
Final value means as t → ∞
I step ( t ) final= 3
5 R
Taking the gradient of I (t) w.r.t time
∂ I (t )
∂ x = −1
2 R ( −R
L ) e
−R
L t
− −1
10 R ( −5 R
L ) e
−5 R
L t
Initial value of gradient at t=0
∂ I (t )
∂ x = 1
L at t=0
A4)
I step ( t )= 3
5 R u ( t )− 1
2 R e
−R
L t
u ( t )− 1
10 R e−5 R
L t
u ( t )
Impulse response h ( t )= d
dt s (t) where s(t) is step response
⇒ 1
2 L e
−R
L t
u ( t ) + 1
2 L e−5 R
L t
u ( t )
A5)
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
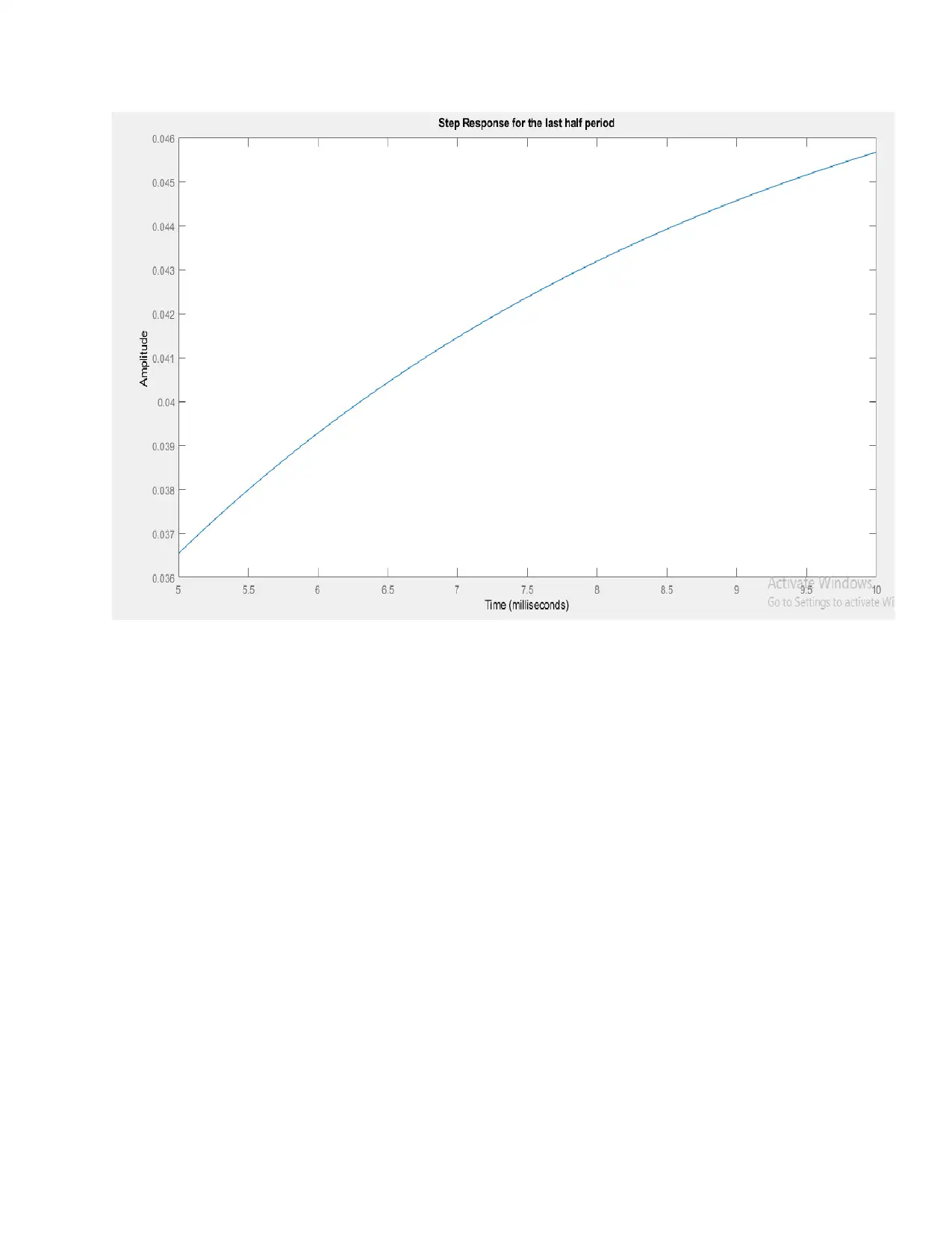
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
A6
From the transfer function and the input given,
I ( s ) =
1
L ( s+ 3 R
L )
s2+6 R
L s+5 ( R
L )
2 ( ω
s2 +ω2 ) where ω
s2+ ω2 =V ( s )
As time tends to infinity, s tends to zero and so,
I ( s )= 12815.9487
256318.9747 ω
ω (rads/s) δ (t) mA, impulsive
10 5
100 0.5
1000 0.05
10000 0.005
From the transfer function and the input given,
I ( s ) =
1
L ( s+ 3 R
L )
s2+6 R
L s+5 ( R
L )
2 ( ω
s2 +ω2 ) where ω
s2+ ω2 =V ( s )
As time tends to infinity, s tends to zero and so,
I ( s )= 12815.9487
256318.9747 ω
ω (rads/s) δ (t) mA, impulsive
10 5
100 0.5
1000 0.05
10000 0.005
A7
V (s )
I (s) =
s2 +6 R
L s+5 ( R
L )2
1
L (s+ 3 R
L ) =
s2 + 72000
53 s +256318.9747
1000
53 s+12815.94874
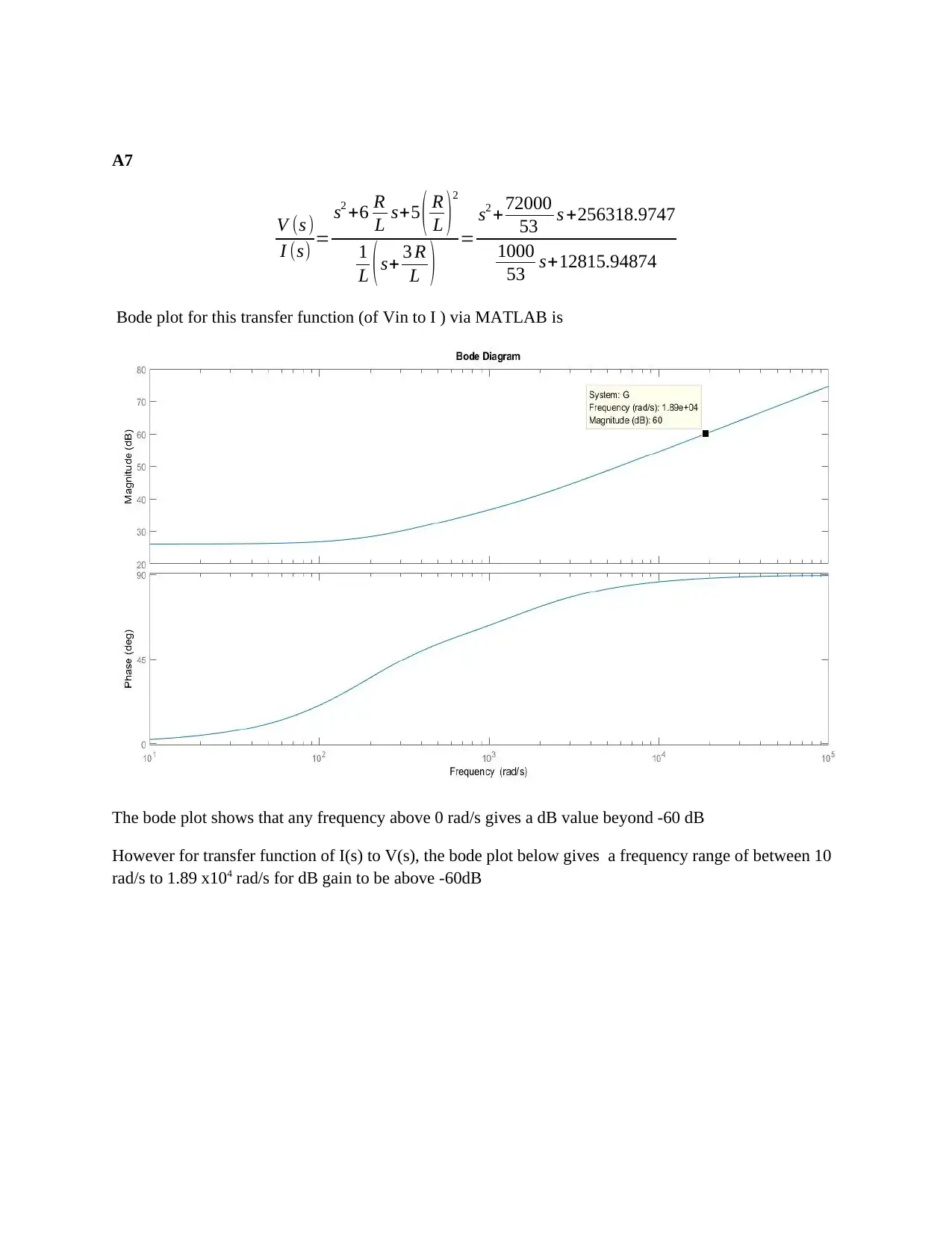
Bode plot for this transfer function (of Vin to I ) via MATLAB is
The bode plot shows that any frequency above 0 rad/s gives a dB value beyond -60 dB
However for transfer function of I(s) to V(s), the bode plot below gives a frequency range of between 10
rad/s to 1.89 x104 rad/s for dB gain to be above -60dB
V (s )
I (s) =
s2 +6 R
L s+5 ( R
L )2
1
L (s+ 3 R
L ) =
s2 + 72000
53 s +256318.9747
1000
53 s+12815.94874
Bode plot for this transfer function (of Vin to I ) via MATLAB is
The bode plot shows that any frequency above 0 rad/s gives a dB value beyond -60 dB
However for transfer function of I(s) to V(s), the bode plot below gives a frequency range of between 10
rad/s to 1.89 x104 rad/s for dB gain to be above -60dB
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
A8
I (s)
V (s )=
1000
53 s+12815.94874
s2 + 72000
53 s +256318.9747
The state space equivalent of this transfer function is
˙x= ( 0 1
−256319 −1358.49 ) x+ (0
1 )u
y= (12815.9 18.868 ) x
Transfer function element poles are:
s1,2=−1132.08∧−226.415
The controllability matrix of the system is:
( 0 1
1 −1358.49 )
The system is not unstable and thus does not require constant real gains to be fed via the feedback path.
2. Part B: Ball and Beam System
Problem B1
The expressions defining the system are
5
7 ¨x +g sin θ−x ˙θ2=0
I (s)
V (s )=
1000
53 s+12815.94874
s2 + 72000
53 s +256318.9747
The state space equivalent of this transfer function is
˙x= ( 0 1
−256319 −1358.49 ) x+ (0
1 )u
y= (12815.9 18.868 ) x
Transfer function element poles are:
s1,2=−1132.08∧−226.415
The controllability matrix of the system is:
( 0 1
1 −1358.49 )
The system is not unstable and thus does not require constant real gains to be fed via the feedback path.
2. Part B: Ball and Beam System
Problem B1
The expressions defining the system are
5
7 ¨x +g sin θ−x ˙θ2=0
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

( m x2 +I ) ¨θ+2 mx ˙x ˙θ+ mgx cos θ=u
Defining the state variables as p1 ( t ) , p2 ( t ) , p3 ( t )∧p4 (t )
Let
p1 ( t ) =x ( t ) p2 ( t ) = ˙x( t)
p3 ( t ) =θ(t )
p4 ( t ) = ˙θ( t)
The state vector is thus defined as,
( p1 ( t )
p2 ( t )
p3 ( t )
p4 ( t ) ) =
( x ( t )
˙x ( t )
θ ( t )
˙θ ( t ) )
Differentiating the state variables,
˙p1 ( t ) = ˙x ( t ) = p2 ( t )
˙p2 ( t ) = ¨x ( t )= 5
7 ( x ˙θ2−g sin θ ) =5
7 ( p1 p4
2−g sin p3 )
˙p3 ( t ) = ˙θ(t)=p4 ( t )
˙p4 ( t ) = ¨θ ( t ) = u−mgx cos θ−2 mx ˙x ˙θ
m x2+I
˙p4 ( t ) = u−mg p1 cos p3−2 m p1 p2 p4
m p1
2+ I
In terms of state variables, the equations of motion can be written as,
˙p=
( p2 ( t )
5
7 ( p1 p4
2−g sin p3 )
p4 ( t )
u−mg p1 cos p3−2 m p1 p2 p4
m p1
2+I
)=f ( p , u)
Defining the state variables as p1 ( t ) , p2 ( t ) , p3 ( t )∧p4 (t )
Let
p1 ( t ) =x ( t ) p2 ( t ) = ˙x( t)
p3 ( t ) =θ(t )
p4 ( t ) = ˙θ( t)
The state vector is thus defined as,
( p1 ( t )
p2 ( t )
p3 ( t )
p4 ( t ) ) =
( x ( t )
˙x ( t )
θ ( t )
˙θ ( t ) )
Differentiating the state variables,
˙p1 ( t ) = ˙x ( t ) = p2 ( t )
˙p2 ( t ) = ¨x ( t )= 5
7 ( x ˙θ2−g sin θ ) =5
7 ( p1 p4
2−g sin p3 )
˙p3 ( t ) = ˙θ(t)=p4 ( t )
˙p4 ( t ) = ¨θ ( t ) = u−mgx cos θ−2 mx ˙x ˙θ
m x2+I
˙p4 ( t ) = u−mg p1 cos p3−2 m p1 p2 p4
m p1
2+ I
In terms of state variables, the equations of motion can be written as,
˙p=
( p2 ( t )
5
7 ( p1 p4
2−g sin p3 )
p4 ( t )
u−mg p1 cos p3−2 m p1 p2 p4
m p1
2+I
)=f ( p , u)

Let constant ball position xo and zero velocity be the operating point of the system. The
corresponding angular velocity of the beam and angle therefore are both zero too. The system’s
operating point is
po =
(xo
0
0
0 )
To maintain this operating point, operating input is required. This is evaluated from the
balancing torque gotten from equating
f ( p , u )=0
Evaluating,
τu =mg xo
τu is the required torque in maintaining the ball at its stationary position xo
Taking the Jacobian of the equation f ( p ,u) with respect to (p), the state vector is
∂ f
∂ p ( p ,u ) =
[ 0 1 0 0
5
7 p4
2 0 −5
7 g cos p3
10
7 x1 x4
0 0 0 1
d f 4
d p1
−2m p1 p4
m p1
2 + I
mg p1 sin p3
m p1
2+I
−2 m p1 p2
m p1
2 +I ]
where , d f 4
d p1
=¿ ¿
At the operating point, the system’s matrix of the state space representation is
A= ∂ f
∂ p ( po ,uo )=
[ 0 1 0 0
0 0 −5
7 g 0
0 0 0 1
−mg
m xo
2+ I 0 0 0 ]With respect to input u, the Jacobian yields
corresponding angular velocity of the beam and angle therefore are both zero too. The system’s
operating point is
po =
(xo
0
0
0 )
To maintain this operating point, operating input is required. This is evaluated from the
balancing torque gotten from equating
f ( p , u )=0
Evaluating,
τu =mg xo
τu is the required torque in maintaining the ball at its stationary position xo
Taking the Jacobian of the equation f ( p ,u) with respect to (p), the state vector is
∂ f
∂ p ( p ,u ) =
[ 0 1 0 0
5
7 p4
2 0 −5
7 g cos p3
10
7 x1 x4
0 0 0 1
d f 4
d p1
−2m p1 p4
m p1
2 + I
mg p1 sin p3
m p1
2+I
−2 m p1 p2
m p1
2 +I ]
where , d f 4
d p1
=¿ ¿
At the operating point, the system’s matrix of the state space representation is
A= ∂ f
∂ p ( po ,uo )=
[ 0 1 0 0
0 0 −5
7 g 0
0 0 0 1
−mg
m xo
2+ I 0 0 0 ]With respect to input u, the Jacobian yields
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

∂ f
∂u ( p ,u ) =
[ 0
0
0
1
m xo
2 + I ]At the operating point, the input matrix (B) of the state space representation is
A= ∂ f
∂u ( po ,uo )=
[ 0
0
0
1
m xo
2+ I ]If the ball position is taken as the output of the system, the output matrix C is given by
C= [ 1 0 0 0 ]
And the feed-forward matrix D is
D= [ 0 ]
The above matrices define the state representation taking the general form,
˙x (t )= Ax ( t ) +Bu (t)
y (t )=Cx ( t ) +D
To simplify the above matrices, the parameters defined by the variables are replaced with the
respective ones of Quanser consulting Ball and Beam system of 2014 as;
xo=0
m=0.11
I =19 x 10−3 kg .m2
g=9.81m s−2
The state space representation of the system is:
˙p ( t ) =
[ 0 1 0 0
0 0 −7 0
0 0 0 1
−56.8 0 0 0 ] p ( t ) +
[ 0
0
0
52.6 ] u(t )
y ( t ) = [1 0 0 0 ] p(t )
Problem B2
∂u ( p ,u ) =
[ 0
0
0
1
m xo
2 + I ]At the operating point, the input matrix (B) of the state space representation is
A= ∂ f
∂u ( po ,uo )=
[ 0
0
0
1
m xo
2+ I ]If the ball position is taken as the output of the system, the output matrix C is given by
C= [ 1 0 0 0 ]
And the feed-forward matrix D is
D= [ 0 ]
The above matrices define the state representation taking the general form,
˙x (t )= Ax ( t ) +Bu (t)
y (t )=Cx ( t ) +D
To simplify the above matrices, the parameters defined by the variables are replaced with the
respective ones of Quanser consulting Ball and Beam system of 2014 as;
xo=0
m=0.11
I =19 x 10−3 kg .m2
g=9.81m s−2
The state space representation of the system is:
˙p ( t ) =
[ 0 1 0 0
0 0 −7 0
0 0 0 1
−56.8 0 0 0 ] p ( t ) +
[ 0
0
0
52.6 ] u(t )
y ( t ) = [1 0 0 0 ] p(t )
Problem B2
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
The above state space representation is converted to the transfer function equivalent using the
relation
H ( s )= P( s)
U ( s)=C(s I− A)−1 B+ D
P(s )
U ( s)= [1 0 0 0 ]
[ s −1 0 0
0 s 7 0
0 0 s −1
56.8 0 0 s ]−1
[ 0
0
0
52.6 ]\
P(s )
U ( s)=H ( s )= 368.2
−s4 +397.6
Transfer function element zeros: none
Transfer function element zeros:
−s4 +397.6=0
s1,2,3,4=−4.46541 ,−4.46541 i , 4.46541i , 4.46541
Since one of the poles (4.46541) lie on the right hand plane, the system is not stable
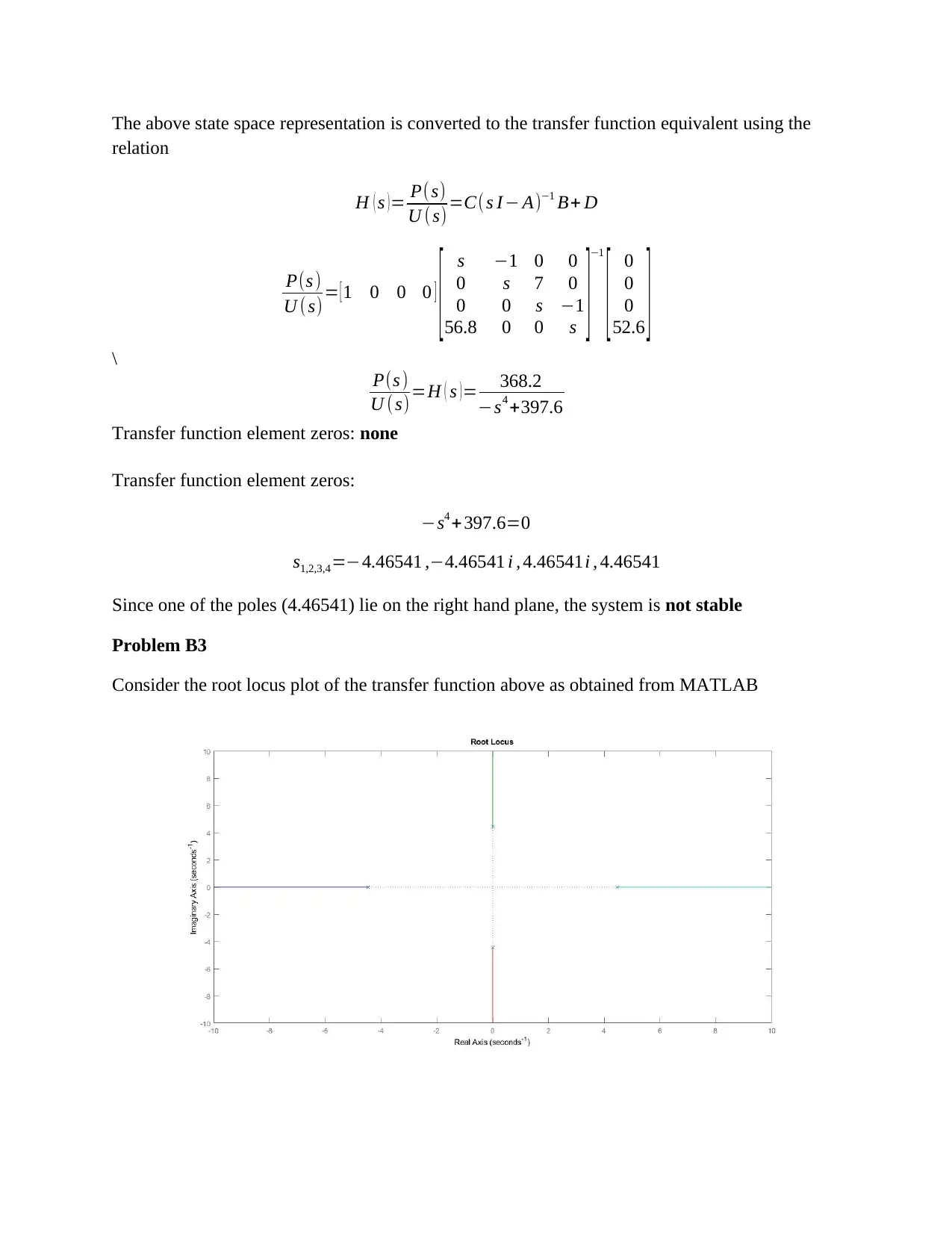
Problem B3
Consider the root locus plot of the transfer function above as obtained from MATLAB
relation
H ( s )= P( s)
U ( s)=C(s I− A)−1 B+ D
P(s )
U ( s)= [1 0 0 0 ]
[ s −1 0 0
0 s 7 0
0 0 s −1
56.8 0 0 s ]−1
[ 0
0
0
52.6 ]\
P(s )
U ( s)=H ( s )= 368.2
−s4 +397.6
Transfer function element zeros: none
Transfer function element zeros:
−s4 +397.6=0
s1,2,3,4=−4.46541 ,−4.46541 i , 4.46541i , 4.46541
Since one of the poles (4.46541) lie on the right hand plane, the system is not stable
Problem B3
Consider the root locus plot of the transfer function above as obtained from MATLAB

It is seen from the root loci that as gain (K) is increased to infinite values, a pole moves from
zero to the right half plane while two poles are on the imaginary axis. A full state feedback
controller must thus be utilized to place all poles in the left half plane of the root locus plot. A
proportional controller cannot realize this pole placement i.e. it can only adjust the overall gain
of the system without interfering with the pole position.
3. Part C
PROBLEM C1
The given system is non-linear as it is described by non-linear differential equations of x (t) and
θ( t)
The state-space representation of the given system yields the state variables x and θ whereas the
input variable isF
The equilibrium point of interest for the inverted pendulum is θ=π
PROBLEM C2
Taking the Laplace transform while assuming zero initial conditions yield
( M +m ) s2 X ( s ) +ml s2 θ ( s ) +bsX ( s ) =F (s)
4
3 l s2 θ ( s ) +s2 X ( s ) =gθ( s)
From the second equation
X ( s )= 1
s2 [g− 4
3 l s2
]θ (s)
Substituting for X ( s ) in the first equation
( M +m ) s2 ∙ 1
s2 [g− 4
3 l s2
]θ ( s ) +ml s2 θ ( s ) +bs ∙ 1
s2 [ g− 4
3 l s2
]θ ( s )=F (s)
( M +m ) [ g− 4
3 l s2
] θ ( s ) +ml s2 θ ( s ) + b
s [ g− 4
3 l s2
] θ ( s ) =F(s)
( ( M +m ) [ g− 4
3 l s2
] +ml s2 + b
s [ g− 4
3 l s2
] ) θ ( s ) =F (s)
⇒ θ ( s )
F( s)= 1
( M + m ) [ g− 4
3 l s2
] + ml s2+ b
s [ g− 4
3 l s2
]
zero to the right half plane while two poles are on the imaginary axis. A full state feedback
controller must thus be utilized to place all poles in the left half plane of the root locus plot. A
proportional controller cannot realize this pole placement i.e. it can only adjust the overall gain
of the system without interfering with the pole position.
3. Part C
PROBLEM C1
The given system is non-linear as it is described by non-linear differential equations of x (t) and
θ( t)
The state-space representation of the given system yields the state variables x and θ whereas the
input variable isF
The equilibrium point of interest for the inverted pendulum is θ=π
PROBLEM C2
Taking the Laplace transform while assuming zero initial conditions yield
( M +m ) s2 X ( s ) +ml s2 θ ( s ) +bsX ( s ) =F (s)
4
3 l s2 θ ( s ) +s2 X ( s ) =gθ( s)
From the second equation
X ( s )= 1
s2 [g− 4
3 l s2
]θ (s)
Substituting for X ( s ) in the first equation
( M +m ) s2 ∙ 1
s2 [g− 4
3 l s2
]θ ( s ) +ml s2 θ ( s ) +bs ∙ 1
s2 [ g− 4
3 l s2
]θ ( s )=F (s)
( M +m ) [ g− 4
3 l s2
] θ ( s ) +ml s2 θ ( s ) + b
s [ g− 4
3 l s2
] θ ( s ) =F(s)
( ( M +m ) [ g− 4
3 l s2
] +ml s2 + b
s [ g− 4
3 l s2
] ) θ ( s ) =F (s)
⇒ θ ( s )
F( s)= 1
( M + m ) [ g− 4
3 l s2
] + ml s2+ b
s [ g− 4
3 l s2
]
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 15
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.
