Modern Control Theory: State Space, Transfer Functions, and Simulink

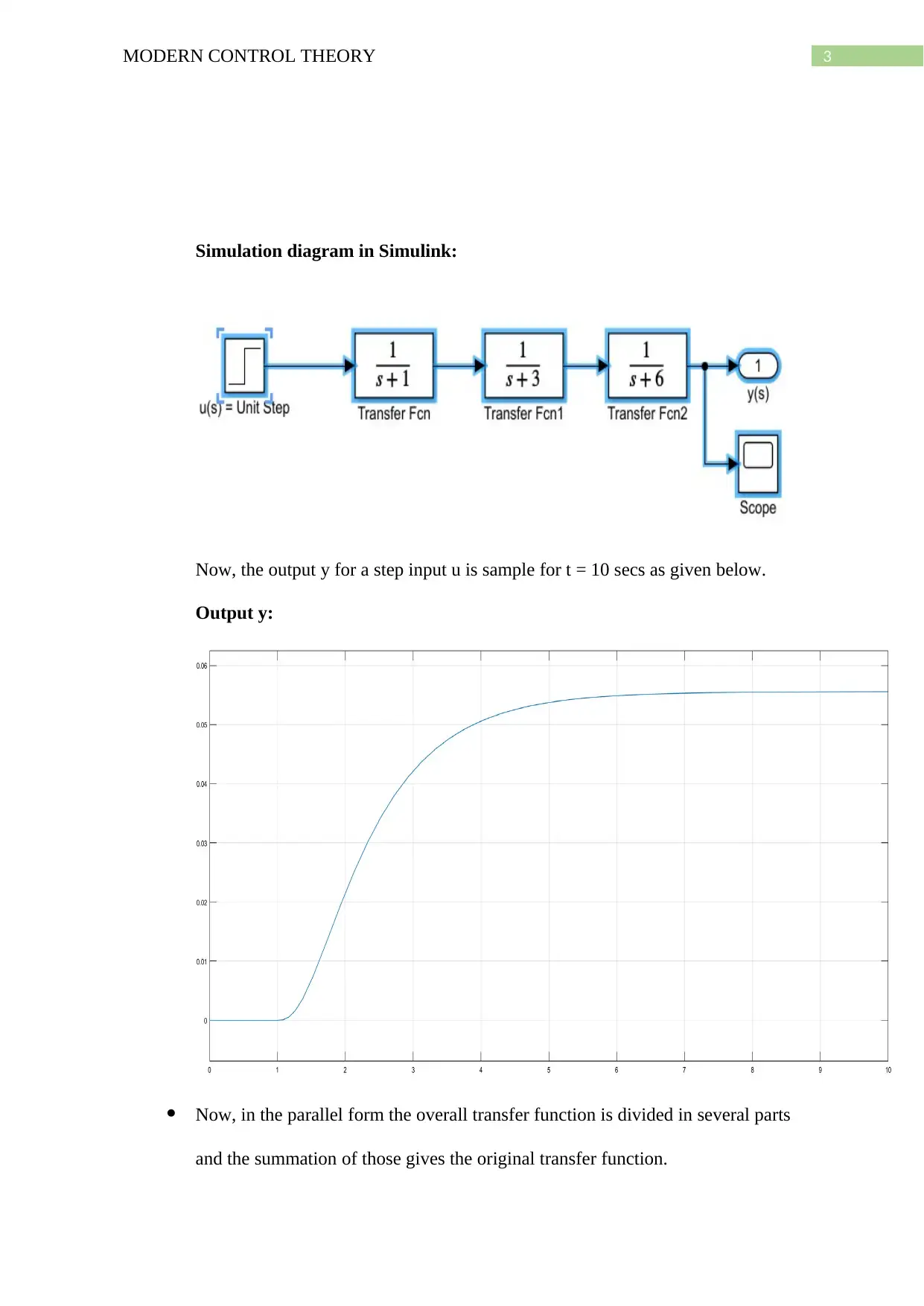
This document provides a comprehensive solution to a Modern Control Theory homework assignment. The solution begins by deriving state-space equations for a two-input, two-output system. It then focuses on a single-input, single-output (SISO) system, deriving state-space equations in controllable canonical form. Furthermore, the assignment explores the factored (cascade) and parallel forms of the transfer function, including the derivation of the state-space representation and Simulink simulation diagrams for each form. The document includes MATLAB code for partial fraction decomposition and presents the output responses for a step input, comparing the results of the parallel and cascade forms to demonstrate their equivalence.

Running head: MODERN CONTROL THEORY
MODERN CONTROL THEORY
Name of the Student
Name of the University
Author Note

1MODERN CONTROL THEORY
1. The two input and two output system is given as follows.
¨y1 +3 ˙y1+ 2 y2=u1+2 u2 +2 ˙u2
¨y2 +4 ˙y1+3 y2= ¨u2+3 ˙u2+u1
Let, y1 = a1. So, ˙y1 =a 1 ' = a2.
a2’= ¨y1=z1
Similarly, let y2 = b1.
b2 = b1’= ˙y2, b2’= ¨y2=z2
The outputs can also be transformed into new variables.
Let, u1 = c1, ˙u1 = c1’ =c2
u2=d 1, ˙u2 = d1’ = d2, ¨u2 = d2’=d3.
Now, the new variables are rewritten in the following way.
a1’ = a2
a2’ = -3*a2 -2*b1 + c1 + 2*d2 + 2*d3
b1’ = b2
b2’ = -4*a2 -3*b1 + d3 + 3*d2 + c1
Hence, the state space model will be
[a 1’
a 2’
b 1’
b 2’ ]=
[0 1 0 0
0 −3 −2 0
0 0 1 0
0 −4 −3 0 ][a1
a2
b1
b 2 ] +
[0 0 0 0
1 0 2 2
0 0 0 0
1 0 3 1 ][c 1
c 2
d 2
d 3 ]
2.
 The transfer function of the SISO system is
y (s )
u (s )= 1
s3 +10 s2 +27 s +18 =T (s )

2MODERN CONTROL THEORY
In general the controllable canonical form of the transfer function of form
y (s )
u (s ) = b 0 ¿ s2+ b 1∗s+b 2
s3 +a 1∗s2+a 2∗s+a3 =T (s)
The equivalent State space model is
q’ = A*q + Bu = [ 0 1 0
0 0 1
−a 3 −a 2 −a1 ] q +
[ 0
0
1 ] u
y = Cq + Du = [ b 2 b 1 b 0 ] q+0∗u
The above matrix representation is the controllable canonical form.
Here, b0= 0, b1 = 0, b2=1, a1 = 10, a2 = 27 and a3 = 18.
Hence, the controllable canonical form is
q’= [ 0 1 0
0 0 1
−18 −27 −10 ] q+ [0
0
1 ]u
y = [ 1 0 0 ] q+0∗u
 Now, in the Factored or cascaded form, the overall transfer function is factored in
several factors and multiplication of those gives the overall transfer function.
y (s )
u (s )= 1
s3 +10 s2 +27 s +18 = 1
s3+s2+ 9 s2+ 9 s+18 s+18 =
1
s2 ( s+1 ) +9 s ( s+1 ) +18(s+1)
= 1
( s+1)(s+3)( s+6) =
1
( s+1)∗1
( s+ 3 ) ∗1
( s+ 6)
So, the poles of the transfer function is s=-6,-3 and -1.

3MODERN CONTROL THEORY
Simulation diagram in Simulink:
Now, the output y for a step input u is sample for t = 10 secs as given below.
Output y:
 Now, in the parallel form the overall transfer function is divided in several parts
and the summation of those gives the original transfer function.

4MODERN CONTROL THEORY
Transfer function (TF) y (s )
u (s ) = 1
s3 +10 s2 +27 s +18
As previously done the poles of the TF is s = -6,-3 and -1.
Hence, TF = A
s +6 + B
s+3 + C
s +1
Now, partial fraction can be easily done using MATLAB.
MATLAB code:
>> b =[1];
>> a =[1 10 27 18];
>> [r,p,k] = residue(b,a)
r =
0.0667
-0.1667
0.1000
p =
-6.0000
-3.0000
-1.0000
k =
[]
Hence, the A, B and C coefficients are 0.0667, -0.1667 and 0.1.
So, TF = 1
s3+10 s2+27 s+18 = 0.0667
s+ 6 + −0.1667
s+3 + 0.1
s +1

5MODERN CONTROL THEORY
Simulation diagram in Simulink:
Output y:
Hence, as seen from above both parallel and cascade representation of the transfer
function provides identical output for same unit step input.

6MODERN CONTROL THEORY