Scheduling and Network Analysis for Maintenance Project Management

This project focuses on network scheduling and analysis within the context of a maintenance project. It includes worked solutions for activities, graphical charts, and detailed explanations. The project addresses constraints such as limited personnel and the requirement to finish tasks once started. It involves completing a table, drawing a network diagram to identify the critical path, and creating bar charts for labor allocation, considering both resource-unconstrained and resource-constrained scenarios. Furthermore, the project analyzes the impact of unexpected worker absence on the project schedule and explores project crashing to optimize duration and costs, including both direct and indirect expenses. The analysis includes calculating estimated times, standard deviations, and probabilities for project completion under various conditions, using critical path method and considering the cost implications of crashing activities.

Networks, scheduling and analysis
What is required? Worked solutions for all activities, with graphical
charts as appropriate with excel sheets attached, with
detailed explanation
When is it due? 30 September
What is it worth? 20% of total marks for the unit
Activity 3A
Shutdowns in major asset intensive organisation are planned in line with Project
Management techniques. The activities required for a small maintenance project are
given in the table, based on maintenance delivery plan.
Constraints are:
• No more than a total of 5 people are available.
• All the people are multi-skilled and inter-changeable
• Once one work is started, it needs to be finished the available people before
they move to the next job
• If a job requires 3 people for 2 days then it needs three people and cannot be
done with 2 people for 3 days.
• Overtime working is not allowed.
3A.1 complete the table and draw a network for the job. Show the critical path
and its length.
Activity People
required at
the same
time
Duratio
n
(days)
EFT LFT Float
1-2 2 2 2 5 3
1-3 2 3 3 3 0
2-4 4 2 4 7 3
2-5 5 3 10 10 5
3-4 3 4 7 7 0
4-5 1 3 10 10 0
(Hinze, 2011)

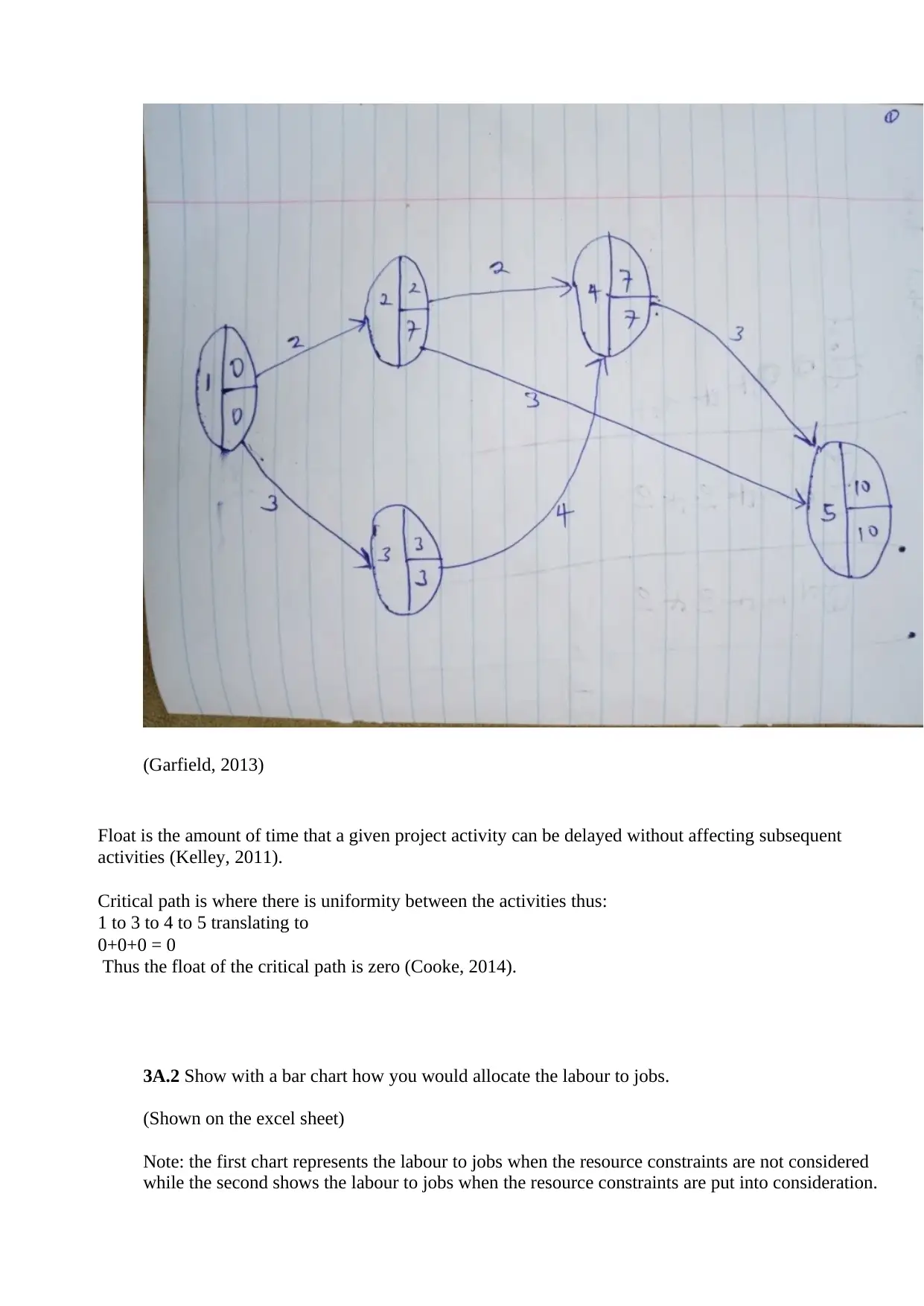
(Garfield, 2013)
Float is the amount of time that a given project activity can be delayed without affecting subsequent
activities (Kelley, 2011).
Critical path is where there is uniformity between the activities thus:
1 to 3 to 4 to 5 translating to
0+0+0 = 0
Thus the float of the critical path is zero (Cooke, 2014).
3A.2 Show with a bar chart how you would allocate the labour to jobs.
(Shown on the excel sheet)
Note: the first chart represents the labour to jobs when the resource constraints are not considered
while the second shows the labour to jobs when the resource constraints are put into consideration.

a. Not considering resource constraints
From the chart the days 3, 4 and 5 require 11, 12 and 8 people respectively showing the conflict of resources
as a result of the fact that five people are available.
b. Considering resource constraints
The chart shows how considering the resource constraints affects the pie labour to job allocation.
3A.3 the project proceeds well, BUT at the start of Day 7, one worker calls by phone
with a medical certificate for 2 days off (i.e. Day 7 and Day 8). Refine the schedule
to show how this affects the project duration. (Note: you cannot go back in time!
Reconfigure the plan from Day 7 onwards).
• Since: If a job requires 3 people for 2 days then it needs three people and
cannot be done with 2 people for 3 days.
For activity
4 to 5
If 1 worker leaves the project will not be affected since resources are available.
The chart remains unaffected.

Activity People
required at
the same
time
Duratio
n
(days)
EFT LFT Float
1-2 2 2 2 5 3
1-3 2 3 3 3 0
2-4 4 2 4 7 3
2-5 5 3 10 10 5
3-4 3 4 7 7 0
4-5 1 3 10 10 0
(Hinze, 2011) (Weist, 2011)
Activity 3B
A plant improvement project in your workplace consists of 10 activities, and is to be
done by contractor. Your estimates of the durations (in weeks) for each of the
activities are shown in the table.
Activit
y No
Optimisti
c time
Most
likely
time
Pessimistic
time
1-2 6 10 12
1-3 10 10 10
1-4 3 5 9
2-6 1 7 13
3-5 2 2 2
3-6 5 4 11
3-7 4 7 10
4-5 6 6 6
5-7 2 8 12
6-7 1 4 7
3B.1 Calculate the estimated time and the standard deviation on that estimate for
each activity.
Activit
y No
Optimisti
c time
Most
likely
time
Pessimistic
time
Estimated
Time
1-2 6 10 12 9.7
1-3 10 10 10 10
1-4 3 5 9 5.3
2-6 1 7 13 7
3-5 2 2 2 2
3-6 5 4 11 5.3

3-7 4 7 10 7
4-5 6 6 6 6
5-7 2 8 12 7.7
6-7 1 4 7 4
(Antil, Woodhead, 2010)
(Excel Sheet)
Mean
ta+4 tm+tb
6 (Kelley, 2009)
Variance = V = б2 = ( tb−ta
6 )
2
Standard deviation= б = ❑
√V (Kaiser, Bartel, 2010)
3B.2 Establish the critical path and semi critical path for the project, the estimated
project completion time and standard deviations.
Activit
y No
Optimisti
c time
Most
likely
time
Pessimistic
time
Estimated
Time
1-2 6 10 12 9.7
1-3 10 10 10 10
1-4 3 5 9 5.3
2-6 1 7 13 7
3-5 2 2 2 2
3-6 5 4 11 5.3
3-7 4 7 10 7
4-5 6 6 6 6
5-7 2 8 12 7.7
6-7 1 4 7 4

Critical path is where there is uniformity between the activities thus:
1 to 2 to 6 to 7
Thus the duration of the project is 20.7 weeks (Fisher, Saisi, Goldstein, 2015)
3B.3 What is the probability of the project taking more than 24 weeks?
ACTIVITY MEAN VARIANCE STANDARD
DEVIATION
1-2 9.7 1
2-6 7 4
6-7 4 1
TOTAL 20.7 6 2.45
P(x ≤ 24)
P ( X −MEAN
STD )❑
≤ ( 24−20.7
2.45 )❑

P(Z ≤ 1.35) (Battersby, 2007)
Using the standard normal distribution table we get;
Expected project completion time from the calculations is : 20.7 weeks
The standard deviation is 2.45
Deviation from mean is 24-20.7= 3.3 weeks
Z= 3.3/2.44 = 1.36
From the z table the probability is 1-0.9131 which translates to 8.7%
3B.4 If the job can be done in 17 weeks, will result in a bonus of $120 000.
What is the likelihood of this happening?
P ( X −MEAN
STD )❑
≤ ( 17−20.7
2.45 )❑
From the standard distribution table we get 0.9332
Which is 93.3%
100% - Answer
100% - 93.3% = 6.7%
3B.5 What completion time should be specified in the contract if you want to be
97% certain that it will be done in that time?
P ( X −MEAN
STD )❑
≤ ( x−20.7
2.45 )❑
We are looking for X given that the value on the standard distribution table is 0.93
Thus 0.93 translates to 1.48 from the table
P(Z ≤ 1.48) thus ( x−20.7
2.45 )= 1.48
X = 25.33 weeks
3B.6 Draw the network for this project in a time-scaled Activity-on Arrow format.

Activity 3C
You are planning for an essential plant safety upgrade project using
your own people. In your planning, based on your experience, you have
assembled the data in the table below:
The only way that the outage can be shortened is by using additional
resources from contractors and crashing any or all activities where that is
possible, but it can be possible at the extra cost as shown in the table
below.
Activity Norm
al
Crashe
d
T e
days
$ cost T c
days
$ cost $ rate/day
1-2 6 6000 3 9000
1-3 4 2000 3 4000
2-4 3 1500 3 n/a
2-5 2 4000 2 n/a
3-4 7 2000 4 5000
4-7 3 1500 1 3500
4-8 5 3000 4 4000
5-6 6 6000 3 9000
6-9 5 2000 2 5000
7-9 7 1000 5 4000
8-9 4 1000 3 2000
3C.1 Draw the network for this job.
NORMAL

CRASHED

3C.2 Mark clearly the critical path. Find the total cost of both
methods of completing the work.
Normal
Critical path is where there is uniformity between the activities thus:
1 to 3 to 4 to 7 to 9
Thus the duration of the project is 21 days.
Total cost is the cost incurred on the critical path which is:
$30,000

Crashed
Critical path is where there is uniformity between the activities thus:
1 to 3 to 4 to 8 to 9
Thus the duration of the project is 14 days.
Total cost
$2,000
(Carruthers, Battersby, 2006)
Total = $30,000+$2,000*21 = $672,000
3C.3 what is the optimum duration of the outage at minimum total cost
when overheads and other indirect costs of $2000 per day are included?
Set out your calculations using the table layout below, and show your
results with an optimisation chart from a spreadsheet.
Adding the indirect costs of $2000 per day
Critical path is where there is uniformity between the activities thus:
1 to 3 to 4 to 7 to 9
Days Crash decision
to reduce time
Crash cost Direct cost Total cost $
21 Normal duration
without crash
30000 72000
20 Crash 3-4 by 1 day 1000 31000 71000