Final Project: Neural Networks and Computed Torque Control in Robotics

This project report details the development and implementation of neural network controllers for robotic control. It begins with building a SIMULINK model of a two-link robot using provided dynamic equations, followed by the implementation of a computed-torque controller (CTC). The core of the project involves using a neural network controller (NNC) to perform the CTC, also implemented in SIMULINK. The report includes the CTC equations and methods, the NN structure, and simulation results. The student generated training data, constructed a feedforward neural network, and analyzed the performance of the CTC controller, including error analysis and NNC training results. The report also discusses the simulation model of the robot, the simulation of the robot's motion and the use of CTC for the robot. The project aims to demonstrate the effectiveness of these control methods in a robotic system, comparing their performance and accuracy. The report also includes the MATLAB code used to generate the neural network and the Simulink design for the neural controller. The results section presents the waveforms of the training data and the results of the CTC controller.

Neutral Networks for Robotic Control
Introduction
To this day, many scholars pay more and more attention to the problem of controlling robots to have a
restricted movement (Cui, et al., 2013). Generally, there is existence of constraints on the input and the output
of the robot system, like the dead-zone, safety specification, and saturation (Liu & Tong, 2016). Uncertainties in
the robot control manipulator that interact with humans and environment poses a challenge since it has some
dynamics and disturbances that are unknown. In the recent past, more researchers and scholars a like have
used the adaptive neutral for suitable schemes of control for the systems that are nonlinear (Cheng, et al.,
2009). Yet some researchers have used adaptive Jacobian scheme for the approximation of unknown schemes
of kinematics for the manipulator. There are some who have used radial basis function of neutral network for
the compensation of the non linear terms that have seem to be complicated closed-loop dynamics of the robot
systems. Another control scheme was devised based on neutral network for the nonlinear systems of affine
which are aligned to the constraints and have a discrete time (Cheng, et al., 2012).
Robot trajectory planning is the most basic element in robotics applications and generally automation.
Generation of trajectories that has some specific features is an important point that ensures some important
results are achieved regarding the quality and an easy performance needed for the motion, especially when the
speeds of operation are high to necessitate any application (Gasparetto, et al., 2012). The robot trajectory is
divided into two categories, the joint space and the cartesian-space trajectories. The joint space trajectory
planning, like the polynomials spline and time-optimal methods. Joint space trajectory planning is commonly
used in robotics for a continuous, and a smooth motion from the one set of n joint angles to the other, for
example when there’s a movement between two separate cartesian poses where the reversed pose solution
yielded two different sets of n joint angles. The joint-space trajectory generation happens at run time for all n
joints simultaneously and independently. Cartesian trajectory planning are trajectories that passes through
specific points, knot points in b-splines. They can also pass through some straight-line paths that are connected
through points. The position and the orientations must be interpolated.
This paper is aimed at using dynamic equations to build a SIMULINK model of the robot that can accepts the
driving torques in robots’ joints and generates positions and velocities of the joints of the robots. There shall
also be a computed-torque controller (CTC) which shall also be done by SIMULINK for the same robot, and the
use of neutral network (NNC) to be able to perform the CTC and implement the NN controller in SIMULINK.
There shall be CTC equations and methods, and CTC implementation in the simulations, the NNC methods
including the NN structure. Then analysis of the results of the CTC controller gains with comparison errors and
NNC training results and check the accuracy of the outcomes.
Simulation Model of the Robot.
Simulation is a method of designing, executing the model and analyzing the implementation output of a real or t
heoretical physical arrangement. Simulation is indeed very prevalent in life; it allows to comprehend reality and
its complexity. In robotics, simulations have some various ways, and with different software which majorly
focuses on the motion of the robot and manipulating it when certain commands are applied to it or set to act in
different environment. Motion simulation have a central role to play among all simulations, they include
kinematics or what is known as dynamic models of the robotic manipulators. The type of models used shall
depend on the aim of the simulation system. For instance, when using the trajectory planning algorithms, they
rely on the kinematic models. On a similar fashion, the development of a cell of a robot is simulated effectively

using kinematic model only. Modelling and simulating a robotic manipulator technique are different and
possible. The only difference is the way the user uses their model. When applying a block diagram simulator, it
requires combination of the blocks and describing the system, and some requires manual coding. When the
system is very complex, it more often brings a lot of issues and overcoming these issues there are techniques
and approaches that exist to automatically develop the kinematic and dynamic model of the robot. The tools
used for simulating robots can be categorized into two: tools that can simulate systems generally, and special
tools made only for robot modelling. The tools that does simulation generally have special user interfaces or
modules and libraries that simplifies the robot development and the environment to which the robot operate
on. The merit of such integrated toolbox is their flexibility to allow you to use other available tools for the
simulation to do other different tasks (Kumar & Narayan, 2011). A case of such is the design system that allows
you to design a control system, study the simulation, and see the results. The major tool of this kind is
MATLAB/Simulink, others are Mathematica, Dymola/Modelica etc.
The robot is as shown in figure 1
The robot uses two arms whose equations are shown, that means there are two torques:
The two toques represent the position controllers and the force controllers.
τ1 =H11 ¨θ1 + H12 ¨θ2+h1+ c1 … … … … … … … … … … … … (1)
τ 2=H12 ¨θ1 + H22 ¨θ2+ h2+ c2 … … … … … … … … … … … …(2)
Where
H11= 1
3 m1 l1
2 +m2 l1
2 + 1
3 m2 l2
2 +m2 l1 l2 cos θ2 … … … … … … … … …(3)
H12= 1
3 m2 l2
2 + 1
2 m2 l1 l2 cos θ2 … … … … … … … … … (4)

H22= 1
3 m2 l2
2 … … … … … … … … …(5)
h1=− ( 2 h ˙θ1 ˙θ2+ h ˙θ2
2 ) … … … … … … … ..(6)
h2 =h ˙θ1
2 … … … … … … … … … … … . ( 7 )
h=1
2 m2 l1 l2 sinθ2 … … … … … … … … … … … … … . ( 8 )
c1= ( 1
2 m1+m2 ) gl1 cos θ1 +1
2 m2 gl2 cos ( θ1+θ2 ) … … … … … … … … …(9)
c2= 1
2 m2 gl2 cos ( θ1 +θ2 ) … … … … … … … … … (10)
Equation (1) and (2) are to be plugged into the Simulink platform to produce the simulation required, but that
will be after plugging in the values of the parameters given, which is of the torque which will show the
movement of the robot. We are also told that the operating range of the robot is made to be
θ ∈ [−π , π ] ( rad ) , ˙θ ∈ [−10,10 ] (rads /sec2 ),∧ ¨θ ∈[−10,10](rad /sec2 )
Parameters Values
Length of the first link (l1) 0.50 (m)
Length of the second link (l2) 0.25 (m)
Mass of the first link (m1) 10.0 (kg)
Mass of the second link (m2) 5.6 (kg)
Torque limit for joint 1 (T1max) ±100.0 (N-m)
Torque limit for joint 2 (T2max) ±50.0 (N-m)
Structural resonant frequency of the robot (fr) 10 (Hz)
We start with equation (3),
H11= 1
3 10(0.5)2 +5.6(0.5)2 + 1
3 5.6 ¿
H11=−3.05
H12= 1
3 ¿
H12=−3.708
H22= 1
3 (5.6)¿
h=0
c1=5.3 gcos θ1 +0.7 g cos ( θ1+θ2 )

c2=0.7 g
h1=0
h2 =0
Therefore
τ1 =3.05+37.08+5.3 g +0.7 g=40.13+6 g
τ1 =40.13+6 g
And
τ 2=0.7 g−35.91
Now we need to construct a neutral network that produces the calculation of the following equations:
We have replaced the ¨θ1=x1; ¨θ2= x2;
y1=H11 ¨θ1+ H12 ¨θ2 +c1
y2=H21 ¨θ1+ H22 ¨θ2 +c2
With the parameters as shown below:
θ ∈ [−π , π ] ( rad ) , ˙θ ∈ [−10,10 ] (rads /sec2 ),∧ ¨θ ∈[−10,10](rad /sec2 )
The code that follows the equations shall be as follows
% =========
% Clear the workspace
% =========
clear all
close all
clc
Numd=1000;
% ==============
% Generating training paterns
% ==============
% Generate 200 random inputs x1 =[-10 10]
H11=-3.05;
H12=-3.708;
H22=0.117;
x1=12*rand(1,Numd)-6;
% Generate 200 random inputs for x2=[-10 10]
x2=2.4*rand(1,Numd)-1.2;
% Generate outputs according to equations
y1=H11(x1)+H12(x2);

%+(5*rand(1,Numd)2.5);
y2=H12(x1)+ H22(x2);
%+(5*rand(1,Numd)2.5);
% ==============
% Construct the NN
% ==============
% For a quick help in Neural network toolbox, you can type 'help
% nnet' in MATLAB command window for a list of available commands to use
% in the NN toolbox.
% Initialise the Neural Network. the NN initialisation is feedforwardnet
% type 'help feedforwardnet' in MATLAB command window for help.
net=feedforwardnet([10,5]); % two hidden layers with 10 and 5 neurons in each
% Set training parameters
net.trainParam.show=50;
net.trainParam.lr=0.05;
net.trainParam.mc=0.95;
net.trainParam.epochs=1000;
net.trainParam.goal=1e-10;
net.trainParam.max_fail=20;
% validation check counts
% ==============
% Start training the NN
% ==============
net=train(net,[x1;x2],[y1;y2]);
% ==============
% Save the training results
% ==============
save step1 net
% ==============
% Test the training results on 20 randomly generated points
% ==============
x1t=12*rand(1,20)-6;
x2t=2.4*rand(1,20)-1.2;
y1t=H11(x1)+H12(x2);
y2t=H12(x1)+H22(x2);
a=sim(net,[x1t;x2t]);
figure(1)
subplot(211)
hold off
plot(a(1,:),'k-o','LineWidth', 1);
hold on
plot(y1t,'r-+','LineWidth',1);
hold off
legend('NN output', 'equation for Y1')
grid
title('NN performance after 1000 iterations')
subplot(212)
hold off
plot(a(2,:),'k-o','LineWidth', 1);
hold on
plot(y2t,'r-+','LineWidth',1);
hold off
legend('NN output', 'equation for Y2')
grid
figure(2)
error1=y1t-a(1,:);

error2=y2t-a(2,:);
hold off
plot(error1,'k','LineWidth',1)
hold on
plot(error2,'r','LineWidth',1);
legend('Y1 error', 'Y2 error')
title('NN prediction error after 1000 iterations')
grid
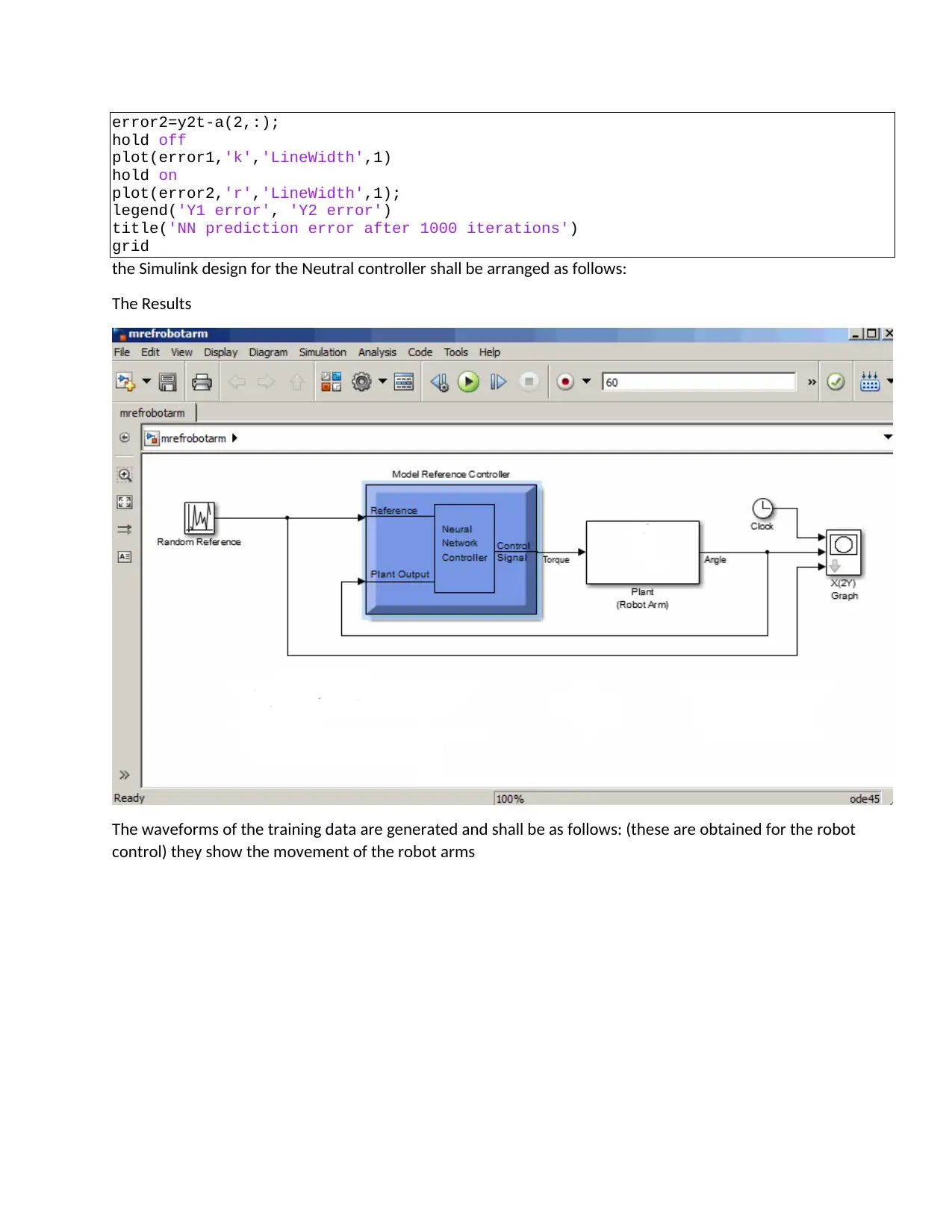
the Simulink design for the Neutral controller shall be arranged as follows:
The Results
The waveforms of the training data are generated and shall be as follows: (these are obtained for the robot
control) they show the movement of the robot arms

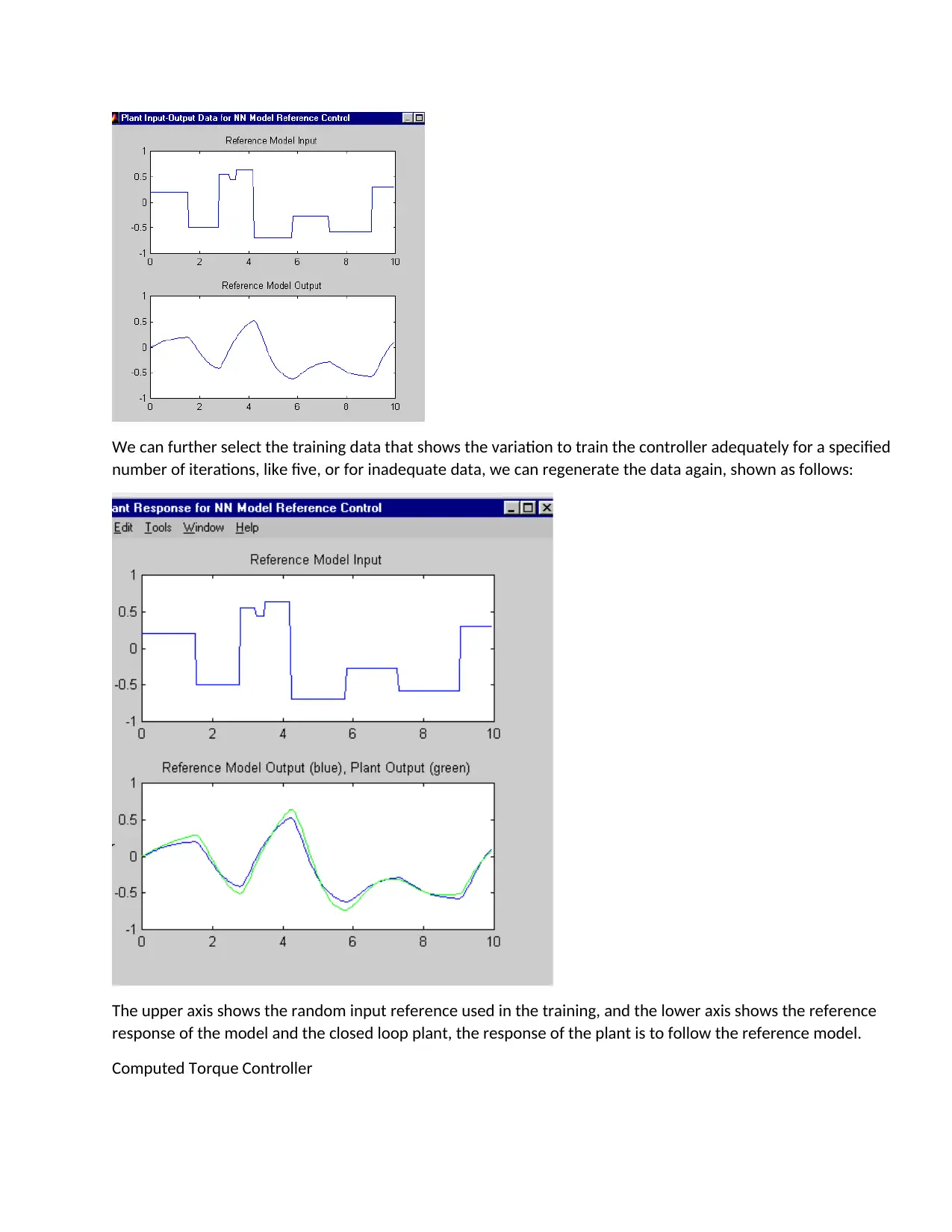
We can further select the training data that shows the variation to train the controller adequately for a specified
number of iterations, like five, or for inadequate data, we can regenerate the data again, shown as follows:
The upper axis shows the random input reference used in the training, and the lower axis shows the reference
response of the model and the closed loop plant, the response of the plant is to follow the reference model.
Computed Torque Controller

Is a prolific non linear controller vastly applied in robotics manipulator. CTC is a feedback-linear technique that
needs a computed torque of the arm by what is known as a non linear law of control. The controller works well
when the physical and dynamic parameters, however, the manipulator part of the robot is varied in the dynamic
parameters, in this condition there’s no acceptable performance of the controller (Vidyasagar & Spong , 2009).
Ideally, many systems that are physical, like the manipulation of robots, the parameters like the time variants
are not known, this is now where CTC can be used for compensation of the robot manipulator dynamic
equation. There’s an ever-growing research of CTC and the application of the robot manipulator reported in
(Siciliano & Khatib, 2018). There has been a functional predictive controller proposed that can be used instead
of the CTC in case there’s a need to track a response in an environment that is uncertain. Nonetheless, the two
controllers can and have been used a linear feedback mechanism, though in a predictive manner that results in
a better performance. CTC that has a parametric model regression is presented and used in an arm of a robot
(Nguyen-Tuong, et al., 2018). The controller in question can pose a problem when the dynamic model is
uncertain. Based on different analyses, CTC is an important nonlinear controller to some systems based on the
linearized feedback and computes the arm torques which are required by a use of non linear control law.
However, when physical and dynamic parameters can be identified the controller works very well; ideally large
amount of systems have misgivings and the controller in sliding mode curbs these challenges posed.
Computed Torque Formulation applied to robot arm
The main idea why CTC is used is to linearize the feedback. Initially the algorithm was referred to as feedback
linearization technique. The working principle is that it assumes that the intended motion trajectory for the
manipulator qt (t ), is found out by the path planner. It defines the error of tracking as:
e ( t )=qd ( t )−qa ( t ) … … … … … … … … … .(11)
Where: e (t) is the plant error, qd (t ) is the variable input desired in the system qa (t) is the real displacement.
The equivalent equation of the linear state-space, which is in the form of x= A x +B U is written as:
x= [0 1
0 0 ]x + [0
1 ]U … … … … … … … … … … … … … .(12)
When the torque equations are as follows:
τ1 =H11 ¨θ1 + H12 ¨θ2+h1+ c1
τ 2=H12 ¨θ1 + H22 ¨θ2+ h2+ c2
[ T1
T2 ] =
[ H11 H12
H21 H22 ] [ ¨θ1
¨θ2 ] + [ h1
h2 ] + [ c1
c2 ] … … … … … … … (13)
We have now obtained the values of H11 , H12 , H22 ,h1∧h2 the values of the ¨θ1∧ ¨θ2 are accelerations for the
joints of the robot. The CTC equation will therefore be:
τ c=
[ H11 H12
H12 H22 ] [ ¨θ1
d + K v 1 ( ˙θ1
d − ˙θ1 ) + K p 1 (θ1
d−θ1)
¨θ2
d + K v 2 ( ˙θ2
d − ˙θ2 ) + K p 2 (θ2
d−θ2) ] + [ h1
h2 ] +
[ c1
c2 ] … … … … …( 14)

The superscript d represents the desired accelerations, velocities and positions; while K p 1 , K p2 , Kv 1 ,∧Kv 2
are control gains that can be calculated using the following characteristics of a second order system:
¨e + Kv ˙e+K p e=0 … … … … … … … … … ( 15 )
Therefore, to achieve the certain damping ratio ζ (≥1)and a natural frequency ωn (≤ 0.5 ωn ),
Discussion