NEF4101 Research Project: CFDST Column Nonlinear Analysis

This project presents a numerical model for analyzing the nonlinear behavior of double square steel tubular short columns filled with concrete (CFDST) under axial compression. The study focuses on the effects of concrete confinement and local buckling of the outer steel tube. The project includes an introduction covering background information, the importance of the research, and objectives. A literature review examines experimental and numerical studies of square CFDST short columns, including discussions on strength, bearing capacity, and finite element modeling. The methodology details steel and concrete stress-strain relationships and the analysis procedure. Results and discussions compare the numerical model with experimental results. The research aims to develop a predictive model for future designs, addressing gaps in existing studies related to local buckling and high-strength materials. The project also considers pre-loads, the confinement of infill concrete, and high-strength materials.

1
Nonlinear Analysis of Double Square Steel Tubular Short Columns Filled with Concrete
Under Axial Compression
Student Name:
Student ID:
Supervisor:
Date of Submission:

2
Contents
Chapter 1. Introduction...........................................................................................................................2
Abstract......................................................................................................................................................2
1.1 Background Information................................................................................................................3
1.2 Importance of the Research study..................................................................................................5
1.3 Objectives of the Research topic.....................................................................................................6
1.4 Layout of This Report.....................................................................................................................6
Chapter 2. Literature Review...................................................................................................................7
2.1 Introduction.....................................................................................................................................7
2.2 Experimental work on square CFDST short columns..................................................................8
2.3 Numerical studies of Square CFDST short columns...................................................................10
2.3.1 Strength Bearing capacity of the composite..........................................................................10
2.3.2 Modelling using Finite Element Method...............................................................................10
2.4 Buckling of CFDST short columns...............................................................................................11
2.4 Conclusion......................................................................................................................................13
Chapter 3. Nonlinear Analysis of square CFDST short columns.........................................................14
3.1 Introduction.............................................................................................................................14
3.2 Methodology.............................................................................................................................16
3.3 Steel stress-strain relationship................................................................................................16
3.4 Stress-strain Relationship for concrete..................................................................................17
3.5 Analysis procedure..................................................................................................................18
3.6 Conclusion................................................................................................................................20
Chapter 4. Results and Discussions........................................................................................................21
4.1 Introduction...................................................................................................................................21
4.2 Comparisons with experimental results.......................................................................................23
4.3 Project Management.....................................................................................................................23
4.4 Resources........................................................................................................................................24
4.5 Risk analysis...................................................................................................................................24
References.................................................................................................................................................25

3
Chapter 1. Introduction
Abstract
The construction of thin-walled square CFDST columns is done by having the space between
double sheet steel tubes filled with concrete. Use of CFDST columns has been widely applied
especially when designing performance-based structures in building projects globally. The
desirable properties of the composite that makes it to be widely adopted are the excellent
ductility and strength when high strength steel is combined with concrete. This research study
therefore seeks to come up with numerical models that can accurately predict the strength and
ductility, and also utilized in the process of designing and analyzing nonlinear square CFDST
columns which are loaded axially. It will contribute a wide body of knowledge since certain gaps
have been identified in the previous studies.
1.1 Background Information
A number of studies have been conducted in the recent past to show that when steel tubes are
filled with concrete to make square CFDST short columns, their performance is significantly
increased to levels exceeding that of conventional columns made of concrete (Mizan, 2018,
p.12). The square CFDST column is a high-performance composite material that is made up of
square tube on the outer side, while the inner tube is double layer and has concrete infill,
resulting into higher resistance to axial loading in short columns. When making a square CFDST
short column, both normal strength or high strength hollow steel tube can be used and filled with
normal strength concrete or a high strength concrete. (VipulKumar, 2013). A high strength
concrete has compressive strengths exceeding 50 Mpa while high strength steels have yield
strengths exceeding 460 Mpa.
It is important to point out that the design concepts acquired in this field of study are not only
elemental for construction purposes but also in the development of International Building Codes
of Practice to enhance structural integrity as well as performance of the structures in the built-up
environment.
In their research work, Qing and Brian (2005) alluded to the fact that square CFDST short
columns are primarily axial-load carrying members in offshore structures, bridges and high-rise
buildings because of their exceptionally higher strengths, ductility and large energy absorption

4
capacities resulting into excellent performance. Their popularity is also partly due to their
relatively lower costs as compared to conventional concrete columns.
When a thin-walled steel column is filled with concrete and subjected to axil loading, the
concrete prevents local inward buckling causing the steel to experience outward local buckling.
This will increase the buckling strength of steel walls and consequently that of the composite
column, ultimately resulting into a high-performance structure.
According to VipulKumar (2013), the use of square CFDST short columns offers a number of
advantages, making them preferred to conventional columns. The steel tubes create a
confinement for the concrete infill. The confinement effects results into increased strength of
concrete and higher ductility of the core within this square cross-sectional area of steel tubes.
The increased strength and ductility results into higher performance of the structure. Another
added advantage of CFDST column is the delay of local bucking of the steel tube caused by the
concrete infill as explained in the previous paragraph. The final advantage which is also essential
is that the steel tubes act as reinforcements in the longitudinal direction as well as formwork for
the concrete infill.
This saves a great deal in financial budgeting of materials and increases the speed of
construction. The formwork created already supports construction loads even prior to pouring of
concrete between the double sheet steel tubes.
As discussed previously, the concrete infill plays a vital role in prevention of inward local
buckling, thus the steel tube can only experience outward local buckling.
Liang and Uy (2000) observed that when examining load-deflection curves of real plates that are
subjected to compressive stresses, there is no bifurcation point. This is explained by the presence
of imperfections in the initial geometry of the real thin steel plates. As a result, it is difficult to
determine the local loads initially subjected to these thin steel plates with imperfections. It is
therefore important to consider the effects of local buckling in the analysis of nonlinear square
concrete-filled double steel tubular short columns.
During construction, steel tubes are erected to several storeys up in a Highrise building before
they are filled with concrete. This means that they are able to support a considerable number of
loads before and after construction supported by the framework established.

5
The effects of these preloads must be taken into consideration when designing square concrete-
filled double steel tubular short columns (VipulKumar, 2013).
Parametric characteristics of square concrete-filled double steel tubular short columns is largely
based on parameters like the ratio of depth to thickness, the eccentricity ratio of loading, column
slenderness ratio, the compressive strength of concrete used as well as yield strength of steel.
Studying all these parameters in this research work would not be cost effective, and would
consume a lot of time.
Conducting a full-scale behavioral analysis of square concrete-filled double steel tubular short
columns would require usage of verified nonlinear inelastic techniques of analysis.
1.2 Importance of the Research study
The use of square concrete-filled double steel tubular short columns has gained popularity in
Highrise structures and bridges in the recent past.
However, there is still limited understanding of their fundamental behavior as a result of
inadequate experimental and numerical research studies covering this composite material.
Thus, efficient design and analysis methods have not been fully developed for square CFDST not
only columns but also other structural members like beams which are also subjected to eccentric
axial loading. The absence of this vital numerical data constitutes a research gap that is one area
to be addressed by this research paper.
High strength concrete is brittle, and its usage in CFDST columns results to reduced ductility of
the column even though the composite material has a relatively higher ultimate strength.
Conversely, usage of high strength thin-walled steel provides economical designs even though
local buckling is possible. Local buckling in steel tubes is associated with a reduction in loads
that the square concrete-filled double steel tubular short columns can support safely.
Even after the initiation of local buckling, loads can still be carried effectively with the thin steel
plates without incidences of failure. As the load is increased gradually, the steel plates undergo
local buckling, a phenomenon referred to as post-local buckling by Liang et al. (2007).
The current nonlinear inelastic methods of analyzing the CFDST composites inadequately
addresses this progressive local buckling, which is yet another research gap to be filled by this
study. These nonlinear inelastic methods do not account for local buckling hence overestimating
the ultimate loads that can be safely carried by the CFDST columns without failure.

6
It is worthwhile mentioning that even the available design codes for instance the Eurocode
4(2004), ACI 318 (2002) and LRFD (1999) have no provisions specifying design of high-
strength CFDST structural members.
Having looked at the highlighted inefficiencies of the previous studies, this research work seeks
to fill the gaps by developing efficient numerical-based models to be adopted in simulation of
non-linear behavior of CFDST composites under axial loading.
These developed simulation models would therefore provide essential information to be used in
the design and analysis of structures which are safer, economical and meets the needs of clients
at the same time. The models to be developed by the study will enable efficiency when analyzing
and designing square concrete-filled double steel tubular short columns using any high strength
concrete or any other grade of concrete as may be appropriate.
1.3 Objectives of the Research topic
The major objective of the study involves coming up with efficient numerical-based models that
can accurately predict the strength and ductility, and also utilized in designing and analyzing
nonlinear square CFDST columns subjected to axial loads. These numerical models are to have
capabilities to account for; (a) pre-loads created by local buckling, (b) confinement of infill
concrete and (c) high strength materials. In order to achieve this main objective task, the
following specific aims needs to be achieved:
 To come up with a numerical model that can be used in the design and nonlinear analysis of
high strength square CFDST short columns with square cross-sectional areas subjected to
axial loading.
 To come up with a numerical model that can be used in the design and nonlinear analysis of
square CFDST short columns subjected to both axial loading and local buckling.
 To come up with a model that can be used in nonlinear analysis of high-strength CFDST
columns under axial loading when they are subjected to both local buckling and pre-load
effects.
 To carry out verification of the developed models by cross-checking them with experimental
data that is already available.
 To conduct in-depth parametric studies so as to examine the effects of various parameters on
the behavior of square concrete-filled double steel tubular short columns when subjected to
axial loads and bending.

7
1.4 Layout of This Report
For convenience and easy understanding of this report, it has been divided into 4 chapters.
Having completed chapter one that deals with the background information on CFDST columns,
chapter 2 presents an in-depth literature review on the nonlinear analysis of square CFDST short
columns subjected to axial loading. A number of journal articles are reviewed that contain
previous similar research work to form the basis of argument. Local and post-local buckling is
then reviewed for both CFDST columns and steel plates. A logical conclusion is then drawn at
the end of the chapter to summarize the literature review in relation to the research paper.
In chapter 3, the stress and strain relationships for both steel and concrete are examined in this
section. Finally, an analysis procedure is developed for the nonlinear square CFDST columns
and relevant conclusions drawn.
Chapter 4 has only two sections, 4.1 and 4.2. It describes the results obtained in the previous
sections and provide well explained discussions on the models developed and interpretations are
made. The second section conducts the comparison of experimental data for verification of the
models developed, and conclusions are made based on these results obtained.

8
Chapter 2. Literature Review
2.1 Introduction
A substantial amount of work in terms of research studies has been done in the area of nonlinear
analysis of square CFDST columns. This section highlights most of the research studies
conducted in this field, and has been used to form the background of this project. It involves a
series of experimental studies and the conclusions that were made in those studies.
Nonlinear techniques of analysis are fundamental in predicting cross sectional ductility
performance and ultimate strengths needed in the design of thin-walled CFDST columns (Qing
Quan, 2008). The current codes {Eurocode 4(2004), ACI 318 (2002) and LRFD (1999)} have
shown discrepancies in their strength predictions since the designs have used different
approaches in designing square concrete-filled double steel tubular short columns.
As much as adoption of this composite is gaining popularity in axil load bearing due to their
high strength, ductility and greater energy absorptions. This is because the steel casing confines
the concrete core increasing its ductility remarkably. The CFDST columns experience outward
local lateral buckling of the outer square steel tube (Klöppel, 1957). However, the effects of local
buckling have not been accounted for in the fiber-based analysis models in the design codes.
Since the analysis of thin-walled square CFDST columns involve a complex interaction of local
and global buckling, its analysis becomes quite challenging.
The most basic characteristics of square concrete-filled double steel tubular short columns is
dictated by a number of parameters like the d/t ratio, slenderness ration, compressive strength of
concrete and the yield strength of steel plates. Even though it is possible to conduct experiments
to investigate the behavior of CFDST columns under different loading conditions, it proves to be
expensive as all the parametric studies need to be conducted in order to conclusively reach a
conclusion, which is also time consuming. Besides, the limited data obtained would not be
sufficient to make a rational conclusion by deriving a theory from the tests that can be utilized
when designing the CFDST composite (Furlong, 1967). A well-developed numerical modelling
can be used in order to prevent the shortcomings of experiments, and used to investigate the
elemental characteristics of square CFDST short columns.

9
2.2 Experimental work on square CFDST short columns
This section highlights a series of experimental work and other research studies that have been
conducted and presents the outcomes of such experiments in a way that relates to this research
project.
It would be interesting to know that the very first experiment to determine the ultimate strength
of square CFDST short columns was done by (Knowles, R. B. and Park, R., 1969). Both steel
and concrete resist axial loading subjected to a square CFDST column (Furlong, 1967). The
experiment he conducted involved testing a number of circular CFDST columns having a ratio of
d/t as 29:98. One of the parameters examined in the study was the effect of thickness of the steel
tube on the ultimate strength of the CFDST columns. A general conclusion in the experiments
was made that when concrete is confined in steel sheets, its ductility is increased and not the
strength. However, a lesser confinement is created when a square steel tube is used, resulting into
lower strength compared to that of circular CFDST column. A recommendation was made that a
CFDST column cross-sectional area can be used as a reinforced concrete section for
determination of axial load-moment interaction diagrams. The circular cross-sectional area of a
CFDST column meant that it has more strength and performs better than a square CFDST short
column in practice.
(Knowles, R. B. and Park, R., 1969) conducted experimental tests using different slenderness ratio to
determine the effect of confinement of infill concrete on the behavior of CFDST columns of
different cross-sectional areas. For the square cross-sectional area of the CFDST column, only
ductility was increased by the confinement and not the ultimate strength. However, for the
circular CFDST column, both the ultimate strength and ductility of the concrete were achieved
by the confinement.
The study also found that increased slenderness decreases the effect created by the confinement
on the concrete core. This results into premature failure of the column by local buckling even
before the compressive strength is increased by strain. During the study, all the columns that
were tested after being subjected to axial loading failed considerably due to column buckling.
However, some cases of the experiment showed that not all the columns failed by local buckling.
The concrete failed after the attainment of the maximum loading. The studies concluded that a
tangent modulus method made reliable and accurate estimations of compressive strength of

10
concrete where the ratios of L/D exceeded 11, and being conservative for those with the same
ratio being lower than 11.
An experimental study conducted by (Hu, H. T., Huang, C. S., Wu, M. H. and Wu, Y. M., 2003)
utilized the analysis method of finite element model (FEM) in the nonlinear analysis of CFDST
short columns to examine the effect of concrete confinement. The research adopted the general-
purpose model of finite element program ABAQUS to examine the inelastic properties of
CFDST short columns. In the nonlinear analysis, both concrete-filled circular and square cross-
sectional areas reinforced with ties were used. A simulation was carried out with the double steel
tubes using model of “elastic-perfectly-plastic” accompanied by the theory of flow whereas the
modelling of concrete was done using “elastic-plastic” theory with associated flow with the rule
isotopic hardening. Since the double steel tubes were subjected to a variety of multiple stresses,
defining the elastic limit was appropriately done by the use of Von Mises yield criterion.
A series of experiments were carried out and the end support orthogonal knife edge were
designed to counteract the effect of friction at the two ends of the column, so as to ensure free
rotational mechanism at the two orthogonal bending planes. The two ends of the composite
CFDST column were pinned and subjected to a single bending curvature. The results obtained
from the experimental study indicated a delay in local buckling of the thin steel walls caused by
the infill concrete core. For a slender column, outward local buckling on all faces of the steel
tube took place at maximum load. Even though a number of experimental studies have been
conducted on the CFDST columns subjected to axial loading, not much is covered on the square
concrete-filled double steel tubular short columns with similar load conditions especially with
steels having higher yield strengths and also high strength concrete. A combination of the two
materials would result to a high strength composite material whose properties would be useful in
the application of civil and structural engineering, thus there is need to come up with numerical
models in their analysis.
2.3 Numerical studies of Square CFDST short columns
2.3.1 Strength Bearing capacity of the composite
The most effective way in solving the axial compressive bearing capacity of a square CFDST
short column is by the use of limit equilibrium (Qing Quang and Brian Uy, 2006). This is
because the method does not give consideration to the way of loading and deformation process.

11
2.3.2 Modelling using Finite Element Method
In analyzing square CFDST composites, software ABAQUS is vital for general purpose analysis
using the Finite Element (FE) method. This requires simulation of the steel tube using the 4-node
shell elements, and using reduced integration i.e. (S4R). for the infill concrete core, modelling is
done using 8-node brick elements (C3D8R), having 3 translation degrees of freedom at each and
every node. Normally, a coefficient friction of 0.25 is used in the simulation models of carbon
steel CFST columns (Han et al., 2007; Tao et al., 2009).
Chromium oxide is chemically stable and is used to cover the surface of a stainless steel for
corrosion resistance, the coefficient of friction and even behavior of the bond between the
stainless-steel tube and concrete core is different from that of conventional carbon CFDST steel
column.
2.4 Buckling of CFDST short columns
When a square CFDST column is subjected to axial compressive forces, the double steel tube
constraints the laterally expanding concrete, creating a compressional effect of the infill concrete
into multidirectional state of compression. This increases the compressive strength and
deformation capacity of the infill concrete, while the infill concrete restrains the local buckling
of the steel tubes. It is for this reason that (Chung, 2010)argues that CFDST columns exhibit
exceptionally high performance.
Unlike the conventional reinforced concrete (RC), the CFDST columns have reinforcement
positioned at the perimeter of the cross section of the column. This maximizes the flexural
capacity of the steel section.
The use of thin-walled steel in CFDST columns to bear compressive strength is often associated
by failure through local buckling. This has an effect of reducing the ductility and compressive
strength of the infill concrete. For a concrete filled square CFDST column, the confinement
effect creates restraints hence the steel tube can only buckle outwards. This is called local
outward buckling.
When a CFDST column composite experiences outward buckling, there is a significant increase
of the critical local buckling strength of the steel and also the load carrying capacity of the
column. Of importance is that the steel plates encasing the concrete also serve as permanent
formwork since the wet concrete is poured into it, thereby increasing the speed of construction
by avoiding prefabricated formworks which take time to erect and remove when one phase of
construction is complete.

12
This formwork also acts as longitudinal reinforcement of the composite hence economical
designs are possible. Because of these properties, the composite is known to have exceptionally
high performance because of its high strength, large amounts of energy absorption and high
ductility as compared to other composite materials. The presence of high strength concrete and
steel plates of high yield strength encourages the adoption of CDFST columns in construction
projects. However, their use is associated with the local instability problem of these thin-walled
steel plates especially when they are subjected to compressive forces and in-plane bending as
explained by (El-Heweity, 2012). When these thin walled steel plates undergo local buckling,
there is a notable reduction in strength and ductility performance, especially when the steel plates
have initial geometric imperfections and residual stresses caused by processes such as welding.
A number of studies have been conducted to explore the local stability of thin-walled steel plates
under compressive forces and in-plane bending mode. A research study done by (Ellobody,
2013) employed the Galerkin’s method to provide a solution to the governing nonlinear
simultaneous differential equation. A similar study done by Rhodes and Harvey (1971) used
steel plates that are simply supported at the loaded edges to examine the effects of load
eccentricity on local and post local buckling of the CFSDT columns, while varying the type of
support conditions at the unloaded edges. A report of load carrying capacity of thin steel plates
with initial imperfections under linearly varying displacement was given by Rhodes et al. (1975).
These studies are consistent in the results observed when local buckling occurs on thin steel
plates, describing the basic behavior of local and post-local buckling of thin-walled steel plates
for square CFDST short columns.
Further studies done by Usami (1993) incorporated energy methods and other analysis methods.
Steel plates that are simply supported were used and subjected to axial compression and bending
moments about major and minor axes. This enabled the development of effective and reliable
numerical width formulas that can be used in the prediction of ultimate strength of the steel
plates. Both analytical and experimental research works have been conducted by Narayanan and
Chan (1985) to investigate the behavior of elastic critical local and post-local buckling strengths
of steel plates. The unique feature of the study was that the steel plates had holes in them and
were then subjected to a varying range of edge displacements. An investigation into the ultimate
loads of a box column with this steel walls was done by (Shanmugam, N. E. and Lakshmi, B. ,
2001). The study also incorporated elements of local buckling in steel plates that were simply
supported and subjected to compressive forces as well as in-plane bending. In all the mentioned
studies above, it is clear that free buckling was allowed in the two lateral directions.

13
The infill concrete in a CFDST column constrains the steel plates. This constraint makes it only
possible for the thin steel plates to undergo local buckling in a unilateral direction when the
composite is under edge compression. The behavior of thin steel plates to experience local
buckling in unilateral direction has led to a number of studies as researchers are curious to
understand its effects on the performance and strength of the composite material. For steel plates
undergoing uniform compression, (Quan, 2017) proposed the use of ultimate strength formula to
be effective for the nonlinear finite element analysis of CFDST short columns.
A research done by Wright (1995) investigated the behavior of steel plates in contact with infill
concrete when they undergo buckling. For the purpose of developing the limiting ratio of width
to thickness for proportioning steel plates, he used the energy method to model reliable
numerical solutions. From the foregoing, the load behavior of thin steel sheets undergoing local
buckling when subjected to axial loading has been a subject of study for quite a long time,
enabling the development of effective mathematical models to solve the underlying problem so
as to efficiently analyze the CFDST columns. (Baishou, 2016) also contributed to the research
body by analyzing the CFDST column subjected to axial compression using the ABAQUS Finite
Element method. They formulated effective width formulas when designing ultimate strength in
columns of this composite material. In a separate study, (Anju Alias and Susan Jacob, 2017)
included these numerical width formulas in the program of fiber element analysis for detailed
analysis of CFDST columns, as this would take into consideration the effect of local buckling of
the thin steel plates. Moreover, the interaction between the formulas of buckling and ultimate
strength is essential for the design of double skin CFDST columns as it accounts for shear and
even biaxial loadings.
It can be pointed out that a number of the above studies that are concerned with the effects of
buckling on steel plates that are in contact with infill concrete are actually acting on plates under
a uniform edge compression.
Further studies should be conducted to come up with analysis methods in predicting the critical
local and post-local buckling strengths when steel plates are unilaterally restrained, then
subjected to non-uniform compressive forces and in-plane bending. Some studies however
present the use of geometric and nonlinear finite element methods of analysis to tackle this
problem. This includes performing experimental studies and based upon the results from the
nonlinear finite element method of analysis, we develop a series of design formulas to calculate
critical local buckling. Similarly, this is also done for the ultimate strength of the steel plates
confining the infill concrete in the CFDST column box. For steel plates that are piled together

14
and subjected to varied compressive loads, a reliable width formula is derived for the prediction
of their ultimate strength. These proposed numerical formulas in buckling shall be compared to
the already available formulas in the later sections of the report.
2.4 Conclusion
Studies were done on the pile of square steel plates having different width to thickness ratio,
geometric imperfections and residual stressed due to welding processes. A variety of loading
conditions were discussed, with the age compression and in-plane bending being explicitly
looked into. A series of design formulas were developed after studying the results on the
nonlinear finite element analysis method.
These formulas would be essential in computation of the critical buckling and ultimate strengths
of these steel plates due to the compression forces acting on them, and also the in-plane bending
effect. For clamped steel, reliable width formulas were modelled to accurately predict the
ultimate design strength when the CFDST columns are subjected to compressive edge forces.
The numerical results obtained points to an indication that when the width to thickness ratio of
steel plates under a predefined stress gradient is increased, there is a corresponding notable
reduction in the following three parameters: (a) lateral stiffness, (b) critical local buckling stress
and (c) the ultimate strength. The studies also prove that these three parameters i.e. lateral
stiffness, critical local buckling stress and the ultimate strength under edge compression are
significantly reduced when the stress gradient coefficient is increased. These design formulas
developed for the design of ultimate strengths of steel plates under edge compression and in-
plane bending shall be compared by other existing models to verify their efficiency and
applicability in the latter sections of the report. They can then be included in the design codes
after approval by the relevant authorities through proper channels as they provide efficient and
economical design solutions.

15
Chapter 3. Nonlinear Analysis of square CFDST short columns
3.1 Introduction
A lot of research work has been done to investigate the parametric behavior of these columns in
order to develop numerical solutions for efficient application in the construction industry. These
studies reveal that the strength and ductility of the composite can be significantly increased by
the use of double layer of steel plates when the composite is subjected to a number of loading
mechanisms. In the work of Han et al (2011) and a similar study conducted by Li et al. (2012)
suggest that both flexural strength, torsional strength and uniaxial strength of the composite
CFDST column is higher thus it performs well when used on structures. The hollow steel section
that replaces the concrete in the composite has considerable effects in the increase of the
strength, since it causes a change in the strength to weight ratio. Studies have also been
conducted to show that the confinement effect created by the concrete infill in the CFDST
column increases the strength of concrete by between 5% to 30%.
Derivation of the bearing capacity formula utilizes the “unified theory” (Zhong, 2006). This
makes the assumption that the concrete infill in the steel tube is taken as a single unified body,
treated as a composite material whose properties changes according to the changes of the
individual material properties of each material forming the composite. These include physical
material parameters, member geometrical parameters, cross sectional area types and the states of
stress in the composite.
In most of the analysis however, the Finite Element Method is highly employed. For stainless
steel modelling using FEM, the Ramberg-Osgood relationship is utilized to efficiently describe
the stress-strain behavior of the material.
Where E0 is taken as the initial elastic modulus and σ0.2 is the 0.2% percentage proof stress. The
strain hardening exponent is n to be determined by σ0.2 and 0.01% proof stress represented as
σ0.01.
Accurate predictions for the behavior of stress-strain in stainless steel can be calculated. This is
only up to the range of 0.2% proof stress, and beyond this point, there are serious inaccuracies
that can only be addressed by modeling the nominal stress-strain behavior of stainless steel at
higher strain levels (Rasmussen, 2003). The Ramberg-Osgood relationship therefore can only be
used up to strains of 0.2% proof stress, and beyond this point, a new expression is given to
account for the higher strains.

16
From the foregoing, it can be demonstrated that three basic parameters from the Ramberg-
Osgood expression to be used in the Rasmussen’s model are the E0, n, and σ0.2. These parameters
are vital in the determination of full-range stress-strain relationship of stainless steel.
All these numerical studies provide reliable models and mathematical formulas that can be used
in the design and analysis of square concrete-filled double steel tubular short columns.
It is a common knowledge that stresses in a material build up as the load increases. For the
composite materials like CFDST columns, the load bearing capacity of the element depends on
the individual yield strengths of the various materials, in this case, concrete and steel. It is
therefore important to look at the individual strengths separately before they are combined in the
composite to act as a single unit.
Both concrete and still exhibit elastic properties up to certain levels before plastic deformation
sets in. since concrete has higher compressive strength while steel is good in tension, a
combination of the two increases the strength of the composite considerably.
To make it excellent, a double steel sheet contributes double the strength of a single sheet. This
section will therefore explore the stress-strain relationships of both concrete and steel to enable
us understand their elastic behavior and plastic behavior and important yield points when such
curves are drawn.
3.2 Methodology
The Denison compression machine having a capacity of 5000kN was used in the laboratory to
conduct the research study. During testing while using concentric loading, the simulated forces
from the load was directly applied to the columns to act axially. To ensure uniformity in load
distribution, a concrete grinder was used to smoothen the two ends of the column. When
conducting the test on CFDST for eccentrically loaded columns, they were pinned at both ends.
3.3 Steel stress-strain relationship
Theoretically, when steel is subjected to axial tensile forces, an elongation occurs. When
subjected to axial load, we develop a stress strain curve.
Note that strain if calculated by dividing the change in length (due to elongation) by the original
length whereas stress is found by dividing the force applied by the cross-sectional area of the
steel bar. When a ductile mild steel is subjected to axial tensile forces, it passes through the
points marked on the diagram which are the limits of each stage:

17
P-Proportional limit: The value of stress and strain remain proportional and it is defined by a
linear equation to obtain the straight line. This is the limit of proportionality. From the origin
(coordinate 0,0) to point P follows Hook’s law
E-Elastic limit: This is the point where the perfectly elastic characteristic of the steel ends. Up to
this point, any deformations caused on the steel by applied forces can go back to their original
shape. However, beyond this point, the elastic nature of the steel ceases to be and permanent
deformations may set in.
Y-Yield stress point: Beyond yield stress point, material deformation is not proportional to the
force applied, since deformation is rapid and elongation increases with little or no force applied.
The material is said to be “yielding” due to build up stresses in the inelastic stage.
At this point, the steel bar cannot regain its original shape and other properties because it has
gone far past elastic range. Stresses in this area are called yield stress.
U-Ultimate stress point: this is the point of maximum stress which a material can bear before
failure occurs. In designs, ultimate stress point can be used and a safety factor included to give
some safety allowance before failure sets in. this is seen to be economical instead of using yield
points of a material for design, even though the latter guarantees safety. Ultimate stress point is
the highest point and shown on the peak of the graph in figure 5. Past this point, the steel has
very negligible strength or zero to bear any further load.
B-Breaking point (Point of rapture): This is the point where material strength breaks and failure
occur finally. It should be noted that failure does not occur at instant since steel is not brittle.
Signs of failure are seen earlier when the structural integrity starts to be compromised by the
large loads. Point B’ is an extrapolation of the stress strain diagram in theory, failure occurs
before this point is reached. It just indicates the nature of the graph and what would have
happened if failure did not occur.
From the previous sections, it has been elaborated that cross-sectional area has significant role in
improving the strength of CFDST columns.
It should also be noted that stresses and strains in an element vary depending on the cross-
sectional areas since area is used to calculate the stress, as it is where the forces act, consequently
affecting the ultimate strength of the composite member.

18
It can be seen that high-strength steel has strength of about 380 Mpa while low strength steel has
strengths of approximately 230 Mpa, both having strain of less than 0.2 indicating that they are
good in tension, making them ideal for usage in CFDST composite to compensate for the lower
tensile strengths of concrete.
3.4 Stress-strain Relationship for concrete
The stress-strain relationship for concrete is linear for the first 30% to 40% of the ultimate load,
before a nonlinear curve sets in, where large strains are recorded as a result of small increases in
stress. The nonlinearity of the curve at this point is as a result of microcracks coalescing at the
interface of paste and aggregates. Concrete reaches ultimate stress when large cracks develop
within the concrete which consists of the coalesced microcracks and those that are in the cement-
paste matrix.
For a normal strength concrete, the ultimate stress has a corresponding strain of about 0.003,
indicating a significantly lower strength than that of steel. This behavior of stress-strain
relationship for axial compression is the same as that in tension. At peak point, concrete can
show a different range of behaviors depending on the type of concrete.
The stress-strain diagrams for sample concrete, both when subjected to compressive and tensile
forces. It can be seen that concrete is brittle and fails much earlier in tensile than in compression.
From the compression graph, the ultimate strength of concrete is about 38 Mpa (normal strength
concrete since high strength has close to 56Mpa) while strain is up to 0.03. From the tensile
graph however, ultimate tensile strength is well below 4Mpa indicating that plain concrete is
significantly weak in tension.
It should be noted that the strength of concrete depends on the number of days from the day of
casting it, thus precautions should be used when determining expected strengths especially the
ultimate strength.
The two materials are then combined to make a composite of CFDST column, having clearly
understood the parametric properties of each material especially the stress strain relationship.
This will enable ease of analysis when the composite is subjected to axial loading and in-plane
bending. The analysis procedure and comparison of the numerical models developed to existing
models is conducted on the next sections.

19
3.5 Analysis procedure
The confinement provided by the steel tubes of the square is minor, and only restricted to the
corners. The confinement effect does not alter the compressive strength of infill core; however, it
has an effect on the improvement of concrete ductility. Equations used are:
Ec = Concrete’s Young’s modulus and can be calculated as:
Curvature ductility index gives the extent of ductility, and can be written as:
In which Фu is the curvature of the CFDST column when the moment reduces to 90% of its
ultimate moment capacity in the post-peak range. The yield curvature Фy is taken as Ф0.75/0.75.
where Ф0.75 stands for the curvature that corresponds to the moment attaining 75% of the column
bending resistance.
CFDST columns in this analysis should be taken as typical composite members with double
layer steel of square cross-section on the outer side infilled with concrete core in the inside. The
confinement effect created by the steel to the concrete infill increases the strength and ductility
of the CFDST column. An ideal core is formed by the infill concrete to bear the compressive
loads thus preventing local buckling of steel inwards which is significantly improved by the
square cross-sectional area.
Even though the CFDST columns are designed to sustain concentric loading, in real practice,
there is progressive eccentric loading acting on the columns.

20
This is brought about by the imperfections in the geometry of the materials used as a result of
manufacturing error or even misalignment in construction process. Because of this, a number of
research studies have analyzed the effects of eccentric loading on mechanical behavior of
CFDST columns. Most of these studies concluded that when CFDST columns are subjected to
eccentric loading, they have excellent ductility performance. However, failure mode occurs due
to bending.
Numerical analysis using Finite Element Method is important in understanding the mechanical
behavior of CFDST columns when simulation is done in an environment where the composite is
subjected to eccentrical compressive loadings.
According to Han et al. (2007), a FEA model can be used to simulate the mechanical behavior of
CFDST columns with hollow sections under eccentric loading.
The freedom degrees for loading on the specimen are constrained apart from displacement along
the z-axis and rotation on the Y-axis to enable application of eccentric load on the CFDST
column.
Modeling for all components (inner concrete core, steel and rigid plates) is done using eight-
node solid elements with reduced integration (C3D8R) also discussed in the previous sections.
This model is used to simulate the quasibrittleness characteristic of the inner concrete core
encased by the double steel plates of square cross-sectional area. Also, the concrete damaged
plasticity (CDP) model in ABAQUS can be similarly used to investigate the plastic nature of
concrete.
In standard modelling equations, As and Ac are the cross-sectional areas of the square steel tube
and the inner concrete core, taken as 11400mm2 and 78400mm2 respectively. The yield strength
of steel and concrete are taken as 340 Mpa and 40 Mpa respectively. Poisson’s ratio in the
modelling is taken as 0.2. For a CFDST column with eccentric loading (e=0), failure is due to
local buckling at the mid-section of the steel. The position of eccentricity can be varied to bring
about a change in the position of buckling.
3.6 Conclusion
The analysis of CFDST columns using finite element found out that confinement effect of infill
concrete by the steel tubes is significantly reduced when eccentricity is increased.

21
Therefore, appropriate models should be used since the existing ones overestimate the strength of
CFDST columns as they tend to ignore the effect of eccentricity on the composite column.

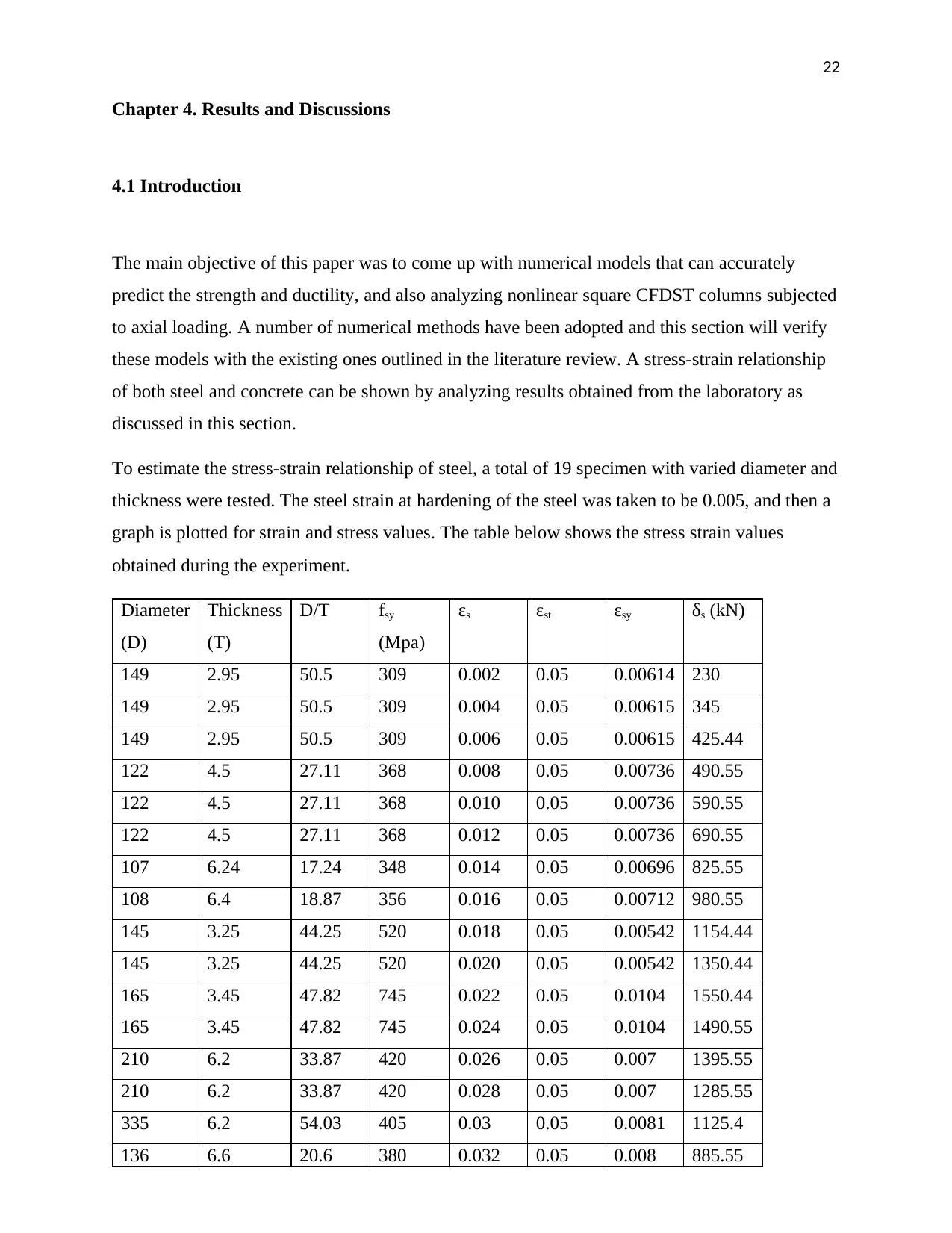
22
Chapter 4. Results and Discussions
4.1 Introduction
The main objective of this paper was to come up with numerical models that can accurately
predict the strength and ductility, and also analyzing nonlinear square CFDST columns subjected
to axial loading. A number of numerical methods have been adopted and this section will verify
these models with the existing ones outlined in the literature review. A stress-strain relationship
of both steel and concrete can be shown by analyzing results obtained from the laboratory as
discussed in this section.
To estimate the stress-strain relationship of steel, a total of 19 specimen with varied diameter and
thickness were tested. The steel strain at hardening of the steel was taken to be 0.005, and then a
graph is plotted for strain and stress values. The table below shows the stress strain values
obtained during the experiment.
Diameter
(D)
Thickness
(T)
D/T fsy
(Mpa)
εs εst εsy δs (kN)
149 2.95 50.5 309 0.002 0.05 0.00614 230
149 2.95 50.5 309 0.004 0.05 0.00615 345
149 2.95 50.5 309 0.006 0.05 0.00615 425.44
122 4.5 27.11 368 0.008 0.05 0.00736 490.55
122 4.5 27.11 368 0.010 0.05 0.00736 590.55
122 4.5 27.11 368 0.012 0.05 0.00736 690.55
107 6.24 17.24 348 0.014 0.05 0.00696 825.55
108 6.4 18.87 356 0.016 0.05 0.00712 980.55
145 3.25 44.25 520 0.018 0.05 0.00542 1154.44
145 3.25 44.25 520 0.020 0.05 0.00542 1350.44
165 3.45 47.82 745 0.022 0.05 0.0104 1550.44
165 3.45 47.82 745 0.024 0.05 0.0104 1490.55
210 6.2 33.87 420 0.026 0.05 0.007 1395.55
210 6.2 33.87 420 0.028 0.05 0.007 1285.55
335 6.2 54.03 405 0.03 0.05 0.0081 1125.4
136 6.6 20.6 380 0.032 0.05 0.008 885.55

23
136 6.6 20.6 380 0.034 0.05 0.0067 705.55
112.5 3.65 30.82 272 0.036 0.05 0.0081 590.5
112.5 3.65 30.82 272 0.038 0.05 0.00764 485.55
Results and discussions
From the results obtained above, it is clear that the stress of steel depends on the ratio of depth to
thickness, revealing the non-linear nature of the steel curve. There is a gradual increase in the
value of diameter to thickness ratio, while stress increases gradually as the strain increases. At a
strain value of 0.022, the stress reaches its peak value and starts to drop gradually. This is useful
information and provides the basis of the understanding of the behavior of CFDST columns.
4.2 Comparisons with experimental results
When axial deformation is increased, the current model proves to be more accurate especially in
the stage of strain-softening. From the table, it can be proved that an accurate prediction can be
achieved since the mean variation between the predicted and experimental values is merely
below 5%.
4.3 Project Management
A project management plan is effective when undertaking any given project since it ensures that
no activity is left out or portioned inadequate time. For this project, a Gantt chart was developed

24
to show the critical activities and give a scheduled plan in advance that would be used
throughout execution of the project. Below is a Gantt chart developed for this project.
Table 1. Gantt chart for the project management
4.4 Resources
A number of resources are needed for this project to succeed. Since it involves estimation of
compressive concrete strengths and tensile strength of steel, a sclerometer from PCE instruments
is needed for concrete strength measurement and a universal testing machine for steel strength.
Materials needed include high strength steel sheets, bags of cement, aggregates, water and access
to laboratory where experiments are to be conducted. ABAQUS general purpose FE package
software is needed for Simulation purposes.
4.5 Risk analysis
Just like any other constructional project, there are risks that can be encountered in the field.
These are injuries that could range from minor bruises to fatalities and should be mitigated at all
costs. Safety precautions to be taken include putting on safety gears like reflectors to enable
machine operators see you clearly, wearing boots to avoid cuts on the lower limbs, putting on
helmets to avoid falling objects from hitting your head and using suspension belts when climbing
on higher parts of the building to erect form work or pour concrete.
A fundamental issue in safety precautions also involves creating an assembly point in case of
emergencies where clear instructions are given. Evacuation measures of workers should also be
available to avoid confusions and running onto each other when a construction hazard occurs.

25
System failures like failure of alarms to go off during emergencies should also be prevented by
continuously updating and maintaining the systems. Finally, for a more effective risk mitigation
plans, there should be adoption of Building Information Modelling (BIM) techniques as they
detect construction hazards in the design stage and give precautionary measures to avoid failure
during the actual execution of the plan.
References

26
Anju Alias and Susan Jacob, 2017. An overview on Concrete Filled Double Skin Steel Tube
(CFDST) column with FRP wrapping. International Research Journal of Engineering and
Technology (IRJET) , April, 4(4), pp. 2081-2083.
Baishou, S. B. a. L., 2016. Axial Compression Properties Nonlinear Analysis on Square Double
Skin Steel Stub Short Columns Filled with Recycled Concrete. Volume 51, pp. 1-6.
Chen, S. F., Teng, J. G. and Chan, S. L., 2001. “Design of biaxially loaded short composite
columns of arbitrary section. Journal of Structural Engineering, 127(6), pp. 678-685.
Chen, S. F., Teng, J. G. and Chan, S. L., 2001. Design of biaxially loaded short composite
columns of arbitrary section. Journal of Structural Engineering, 127(6), pp. 678-685.
Chengyong, W., 2016. Nonlinear analysis and design of concrete-filled dual steel tubular
columns under axial loading. Steel and Composite Structures, February, 20(3), pp. 571-597 .
Choi, K. K. and Xiao, Y., 2010. Analytical studies of concrete-filled circular steel tubes under
axial compression. Journal of Structural Engineering, 136(5), pp. 565-573.
Chung, J., Tsuda, K. and Matsui, C., 1999. High-strength concrete filled square tube columns
subjected to axial loading. Kochi, Japan, s.n., pp. 955-960.
Chung, K. S., Kim, J. H. and Yoo, J. H. , 2012. Prediction of hysteretic behavior of high-strength
square concrete-filled steel tubular columns subjected to eccentric loading. International Journal
of Steel Structures, 12(2), pp. 243-252.
Chung, K., Chung, J. and Choi, S. , 2007. Prediction of pre- and post-peak behavior of concrete-
filled square tube columns under cyclic loads using fiber element method. Thin-Walled
Structures, 45(9), pp. 747-758.
Chung, K., 2010. Prediction of pre- and post-peak behavior of concrete-filled circular steel tube
columns under cyclic loads using fiber element method. Thin-Walled structures, 48(2), pp. 167-
178.
Ebrahim Farajpourbonab and Sunil Kute, 2019. STRENGTH AND HYSTERESIS BEHAVIOR
OF CFDST COLUMNS WITH OCTAGON AND POLYGON STEEL SECTIONS. Journal of
Structural Engineering, March, 45(6), pp. 565-573.
EI-Tawil, S., Sanz-Picón, C. F. and Deierlein, G. G. , 1995. Evaluation of ACI 318 and AISC
(LRFD) strength provisions for composite beam-columns. Journal of Constructional Steel

27
Research, 34(1), pp. 103-123.
El-Heweity, M. M., 2012. On the performance of circular concrete-filled high strength steel
columns under axial loading. Alexandria Engineering Journal, 51(2), pp. 109-119.
Ellobody, E. and Ghazy, M. F. , 2012. “Experimental investigation of eccentrically loaded fibre
reinforced concrete-filled stainless steel tubular columns. Journal of Constructional Steel
Research, Volume 76, pp. 167-176.
Ellobody, E. and Ghazy, M. F, 2012. Tests and design of stainless steel tubular columns filled
with polypropylene fibre reinforced concrete. Singapore, s.n.
Ellobody, E., Young, B. and Lam, D., 2006. Behaviour of normal and high strength concrete-
filled compact steel tube circular stub columns. Journal of Constructional Steel Research, 62(7),
pp. 706-715.
Ellobody, E., 2013. Numerical modelling of fibre reinforced concrete-filled stainless steel
tubular columns. Thin-Walled Structures, Volume 63, pp. 1-12.
Eurocode, 1992. Design of steel structuresm Part 1.1 General rules and rules for Buildings.
Farajpourbonab, E., 2017. EFFECTIVE PARAMETERS ON THE BEHAVIOR OF CFDST
COLUMNS. Journal of Applied Engineering Scienc, 15(1), pp. 99-108.
Fujimoto, T., Mukai, A., Nishiyama, I. and Sakino, 2004. Behavior of eccentrically loaded
concrete-filled steel tubular columns. Journal of Structural Engineering, 130(2), pp. 203-212.
Furlong, R. W., 1967. Strength of steel-encased concrete beam columns. Journal of the
Structural Division, 93(5), pp. 113-124.
Gajalakshmi, P. and Helena, H. J. , 2012. Behaviour of concrete-filled steel columns subjected to
lateral cyclic loading. Journal of Constructional Steel Research, Volume 75, pp. 55-63.
Ge, H. and Usami, T., 1992. Strength of concrete-filled thin-walled steel box columns:
experiment. Journal of Structural Engineering, 118(11), pp. 3036-3054.
Giakoumelis, G. and Lam, D., 2004. Axial capacity of circular concrete-filled tube columns.
Journal of Constructional Steel Research, 60(7), pp. 1049-1068.
Guo, L., Zhang, S. and Xu, Z. , 2011. Behaviour of filled rectangular steel HSS composite
columns under bi-axial bending. Advances in Structural Engineering, 14(2), pp. 295-306.

28
Hajjar, J. F. and Gourley, B. C. , 1996. Representation of concrete-filled steel tube cross-section
strength. Journal of Structural Engineering, 122(11), pp. 1327-1335.
Han, L. H., Tao, Z. and Yao, G. H., 2008. Behaviour of concrete-filled steel tubular members
subjected to shear and constant axial compression. Thin-Walled Structures, 46(7-9), pp. 765-780.
Han, L. H., 2002. Tests on stub columns of concrete-filled RHS sections. Journal of
Constructional Steel Research, 58(3), pp. 353-372.
Han, L. H., 2007. Theory and practice of concrete-filled steel tubular structure. Beijing, China:
s.n.
He Zhang, Kai Wu , Chao Xu, Lijian Ren, and Feng Chen, 2019. Buckling Analysis and Section
Optimum for Square Thin-Wall CFST Columns Sealed by Self-Tapping Screws. Advances in
Civil Engineering, 15 January, Volume 2019, pp. 1-14.
Hu, H. T., Huang, C. S., Wu, M. H. and Wu, Y. M., 2003. Nonlinear analysis of axially loaded
concrete-filled tube columns with confinement effect. Journal of Structural Engineering,
129(10), pp. 1322-1329.
Klöppel, V. K. G. W., 1957. An investigation of the load carrying capacity of concrete filled
steel tubes and development of design formula. Der Stahlbau, 26(2), pp. 44-50.
Knowles, R. B. and Park, R., 1969. Strength of concrete-filled steel tubular columns. Journal of
Structural Division, 95(12), pp. 2565-2587.
Lakshmi, B. and Shanmugam, N. E., 2002. Nonlinear analysis of in-filled steel-concrete
composite columns. Journal of Structural Engineering, 128(7), pp. 922-933.
Liew, J. Y. R. and Xiong, D. X. , 2009. Effect of preload on the axial capacity of concrete-filled
composite columns. Journal of Constructional Steel Research, 65(3), pp. 709-722.
Liew, J. Y. R. and Xiong, D. X. , 2012. Ultra-high strength concrete filled composite columns
for multi-storey building construction. Advances in Structural Engineering, 15(9), pp. 1487-
1504.
Matsui, C., Tsuda, K. and Ishibashi, Y., 1995. Slender concrete filled steel tubular columns
under combined compression and bending. Singapore, Pergamon, s.n., pp. 29-36.
Mizan Ahmed, Qing Quan and Vipulkumar Patel, 2018. Nonlinear Analysis of Rectangular
Concrete-Filled Double Steel Tubular Short columns incorporating local buckling. Engineering

29
Structures, 11 August, 175(2018), pp. 13-26.
Mizan Ahmed, Qing Quan and Vipulkumar Patel, 2020. Experimental and numerical
investigationsof eccentrically loaded rectangular concrete-filled double steel tubular column.
Journal of construction steel Research, 167(105949), pp. 1-9.
Mostafa Fahmi Hassanein, Mohamed Elchalakani and Vipulkumar Ishvarbhai Patel, 2017.
Overall buckling behaviour of circular concrete-filled dual steel tubular columns with stainless
steel external tubes. Thin-Walled Structures, June.pp. 1-65.
Mursi, M. and Uy, B. , 2006. Behaviour and design of fabricated high strength steel columns
subjected to biaxial bending part I: Experiments. Advanced Steel construction, 2(4), pp. 288-313.
Mursi, M. and Uy, B. , 2006. Behaviour and design of fabricated high strength steel columns
subjected to biaxial bending part II: Analysis and design codes. Advanced Steel Construction,
2(4), pp. 314-354.
Patel, V. I., 2013. Nonlinear Inelastic Analysis of Concrete-Filled Steel Tubular Slender Beam-
Columns. January.
QifengShan, JingmingCai , XiaopengLi and Jiawei Tan, 2019. Analysis of Concrete-Filled
Square Steel Tube Short Columns under Eccentric Loading. Mathematical Problems in
Engineering, 20 June, Volume 2019, pp. 1-12.
Qing Quan and Brian Uy, 2006. Nonlinear analysis of concrete-filled thin-walled steel box
columns with local buckling effects. Journal of constrcution steel Research, Volume 62, pp.
581-591.
Qing Quan and Brian Uy, 2012. Nonlinear analysis of concrete-filled thin-walled steel box
columns with local buckling effects. pp. 1-36.
Qing Quan and Uy, 2000. Theoretical study on the post-local buckling of steel plates in concrete-
filled box columns. Computers and structures, 75(2000), pp. 479-490.
Qing Quan, Vipulkumar Patel and Muhammad Hadi, 2012. Biaxially loaded high-strength
concrete-filled steel tubular slender beam-columns, Part 1: Multiscale simulation. Journal of
construction steel Research, 75(2012), pp. 64-71.
Qing Quang and Brian Uy, 2006. Local buckling of steel plates in concrete-filled thin-walled
steel tubular beams-columns. Journal of constructional steel Research, 26 May, Volume 63, pp.

30
396-405.
Quan, Q., 2009. Performance-based analysis of concrete-filled steel tubular beam-columns, Part
1: Theory and Algoriths. Journal of constructionsteel Research, 65(2009), pp. 363-372.
Quan, Q., 2009. Performance-based analysis of concrete-filled steel tubular beam-columns, Part
2: Verifications and Applications. Journal of constructional Steel Research, 65(2009), pp. 351-
363.
Quan, Q., 2017. Nonlinear analysis of circular double-skin concrete-filled steel tubular columns
under axial compression. Engineering Structures, Volume 131, p. 639‐650. .
Roylance, D., 2008. MECHANICAL PROPERTIES OF MATERIALS. s.l.:s.n.
Sakino, K., Nakahara, H., Morino, S. and Nishiyama, I., 2004. Behavior of centrally loaded
concrete-filled steel-tube short columns. Journal of Structural Engineering, 130(2), pp. 180-188.
Schneider, S. P., 1998. Axially loaded concrete-filled steel tubes. Journal of Structural
Engineering, 124(10), pp. 1125-1138.
Shah, D. k., 2014. Parametric Study of Concrete Filled Steel Tube Column. International
Journal of Engineering Development and Research, 2(2), pp. 1678-1682.
Shahiron Shahidan Sharifah Salwa Mohd Zuki, Choong Kok Keong and J. Jayaprakash, 2016.
REPAIRED OF FIRE-DAMAGED CONCRETE-FILLED DOUBLE SKIN STEEL TUBULAR
(CFDST) COLUMNS WITH FIBER REINFORCED POLYMER (FRP). ARPN Journal of
Engineering and Applied Sciences, March.11(6).
Shanmugam, N. E. and Lakshmi, B. , 2001. State of the art report on steel-concrete composite
columns. Journal of Constructional Steel Research, 57(10), pp. 1041-1080.
Shaohua CHEN and Toshimi KABEYASAWA, 2004. AVERAGE STRESS-STRAIN
RELATIONSHIP OF STEEL BARS EMBEDDED IN CONCRETE. Vancouver, Canada, s.n., pp.
1-8.
William E. Luecke, J. David McColskey, Christopher N. McCowan and Richard J. Fields, 2005.
Federal Building and Fire Safety Investigation of the World Trade Center Disaster: Mechanical
Properties of Structural. Washington D.C : National Institute of Standards and Technology .
Xuetao Lyu, Yang Xu, Qian Xu and Yang Yu, 2019. Axial Compression Performance of Square
Thin Walled Concrete-Filled Steel Tube Stub Columns with Reinforcement Stiffener under

31
Constant High-Temperature. Materials, 2 April, 12(1098), pp. 1-22.
Zhong Tao and Lin-Hai Han, 2006. Behavior of concrete-filled double skin rectangular steel
tubular beamcolumns. Journal of Constructional Steel Research, July, 62(7), pp. 631-646..
Zhong Tao, Brian Uy, Fei-Yu Liao and Lin-Hai Han , 2011. Nonlinear analysis of concrete-filled
square stainless steel stub columns under axial compression. Journal of Constructional Steel
Research , 67(11), pp. 1719-1732. .