ITC544 Computer Architecture and Organization: Boolean Algebra Proof
VerifiedAdded on 2023/06/13
|9
|831
|251
Homework Assignment
AI Summary
This assignment solution covers fundamental concepts in computer architecture and organization. It includes number system conversions between different bases such as decimal, binary, octal, and hexadecimal. The solution demonstrates the conversion process with detailed steps. Additionally, the assignment addresses Boolean algebra, providing proofs for given expressions using truth tables and De-Morgan's laws. Concepts like one's complement and two's complement representations are also explored. Desklib offers a wide range of academic resources, including solved assignments and past papers, to support students in their studies.

Running head: COMPUTER ARCHITECHTURE AND ORGANIZATION
Computer Architecture and Organization
Full name:
Student ID:
Subject Code: ITC544
Author’s Note
Computer Architecture and Organization
Full name:
Student ID:
Subject Code: ITC544
Author’s Note
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

1
COMPUTER ARCHITECHTURE AND ORGANIZATION
Table of Contents
Question 1:.......................................................................................................................................2
a.) Determining the value of base x if (152) x = (6A) 16............................................................2
b) Conversions.............................................................................................................................2
c) Representation of value..........................................................................................................5
Question 2:.......................................................................................................................................5
a) Prove........................................................................................................................................5
b) Using basic Boolean algebra identities for Boolean variables x, y, and z, for prove..............7
c) Prove:......................................................................................................................................7
COMPUTER ARCHITECHTURE AND ORGANIZATION
Table of Contents
Question 1:.......................................................................................................................................2
a.) Determining the value of base x if (152) x = (6A) 16............................................................2
b) Conversions.............................................................................................................................2
c) Representation of value..........................................................................................................5
Question 2:.......................................................................................................................................5
a) Prove........................................................................................................................................5
b) Using basic Boolean algebra identities for Boolean variables x, y, and z, for prove..............7
c) Prove:......................................................................................................................................7

2
COMPUTER ARCHITECHTURE AND ORGANIZATION
Answer to Question 1:
a.) Determining the value of base x if (152) x = (6A) 16
Let the value of base be X,
Given,
(152) x = (6A) 16
Or, X^2 + 5X + 2*X = 6*16 + A
Or, X^2 + 5X + 2*X = 6*16 + 10
X2 + 5X + 2 = 106
X^2 + 5X- 104 = 0
X^2 + 13X- 8X – 104 = 0
X (X + 13) – 8(X + 13) = 0
(X - 8) (X + 13) = 0
X = 8 and X = -13
Hence, X is 8.
The value of the base is 8.
b) Conversions
i) BED16 converting to base-3
Solution:
COMPUTER ARCHITECHTURE AND ORGANIZATION
Answer to Question 1:
a.) Determining the value of base x if (152) x = (6A) 16
Let the value of base be X,
Given,
(152) x = (6A) 16
Or, X^2 + 5X + 2*X = 6*16 + A
Or, X^2 + 5X + 2*X = 6*16 + 10
X2 + 5X + 2 = 106
X^2 + 5X- 104 = 0
X^2 + 13X- 8X – 104 = 0
X (X + 13) – 8(X + 13) = 0
(X - 8) (X + 13) = 0
X = 8 and X = -13
Hence, X is 8.
The value of the base is 8.
b) Conversions
i) BED16 converting to base-3
Solution:
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

3
COMPUTER ARCHITECHTURE AND ORGANIZATION
= B * 16*16 + E * 16 + D
= 2816 + 224 + 13
= (3053)10
(3053)10 =
3 3053
3 1017 2
3 339 0
3 113 0
3 37 2
3 12 1
3 4 0
3 1 1
So, (BED)16 = (11012002)3
ii) 3217 into 2-base (binary) representation
Solution:
(321)7 = (3 * 72) + (2 * 71) + (1 * 70)
= (162)10
Again, (162)10 =
2 162
COMPUTER ARCHITECHTURE AND ORGANIZATION
= B * 16*16 + E * 16 + D
= 2816 + 224 + 13
= (3053)10
(3053)10 =
3 3053
3 1017 2
3 339 0
3 113 0
3 37 2
3 12 1
3 4 0
3 1 1
So, (BED)16 = (11012002)3
ii) 3217 into 2-base (binary) representation
Solution:
(321)7 = (3 * 72) + (2 * 71) + (1 * 70)
= (162)10
Again, (162)10 =
2 162
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

4
COMPUTER ARCHITECHTURE AND ORGANIZATION
2 81 0
2 40 1
2 20 0
2 10 0
2 5 0
2 2 1
2 1 0
Hence, (162)10 = (10100010)2
iii) (1235)10 conversion to octal representation
Solution:
8 1235
8 154 3
8 19 2
8 2 3
Hence, (1235)10 = (2323)8
iv) 21.218 conversion to decimal representation
Solution:
21.218 = (2 * 81) + (1 * 80). (2 * 8-1) + (1 * 7=8-2)
= 17 + 0.25 + 0.015625
COMPUTER ARCHITECHTURE AND ORGANIZATION
2 81 0
2 40 1
2 20 0
2 10 0
2 5 0
2 2 1
2 1 0
Hence, (162)10 = (10100010)2
iii) (1235)10 conversion to octal representation
Solution:
8 1235
8 154 3
8 19 2
8 2 3
Hence, (1235)10 = (2323)8
iv) 21.218 conversion to decimal representation
Solution:
21.218 = (2 * 81) + (1 * 80). (2 * 8-1) + (1 * 7=8-2)
= 17 + 0.25 + 0.015625

5
COMPUTER ARCHITECHTURE AND ORGANIZATION
= 17.265625
c) Representation of value
i) One's complement
Highest Value is 011
Lowest Value is 100
ii) Two's complement
Highest Value is 011
Lowest Value is 101
iii) Signed Magnitude
Highest Value is 011
Lowest Value is 111
Question 2:
a) Prove
The expression for the logic diagram is: (a.b)’
Truth table of the expression is provided below:
A b a.b (a.b)’
0 0 0 1
COMPUTER ARCHITECHTURE AND ORGANIZATION
= 17.265625
c) Representation of value
i) One's complement
Highest Value is 011
Lowest Value is 100
ii) Two's complement
Highest Value is 011
Lowest Value is 101
iii) Signed Magnitude
Highest Value is 011
Lowest Value is 111
Question 2:
a) Prove
The expression for the logic diagram is: (a.b)’
Truth table of the expression is provided below:
A b a.b (a.b)’
0 0 0 1
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

6
COMPUTER ARCHITECHTURE AND ORGANIZATION
0 1 0 1
1 0 0 1
1 1 1 0
The expression of the logic diagram
a’ + b’
The truth table for the expression is provided below:
A b a’ b’ a’ + b’
0 0 1 1 1
0 1 1 0 1
1 0 0 1 1
1 1 0 0 0
Hence, LHS = RHS (Proved)
COMPUTER ARCHITECHTURE AND ORGANIZATION
0 1 0 1
1 0 0 1
1 1 1 0
The expression of the logic diagram
a’ + b’
The truth table for the expression is provided below:
A b a’ b’ a’ + b’
0 0 1 1 1
0 1 1 0 1
1 0 0 1 1
1 1 0 0 0
Hence, LHS = RHS (Proved)
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
7
COMPUTER ARCHITECHTURE AND ORGANIZATION
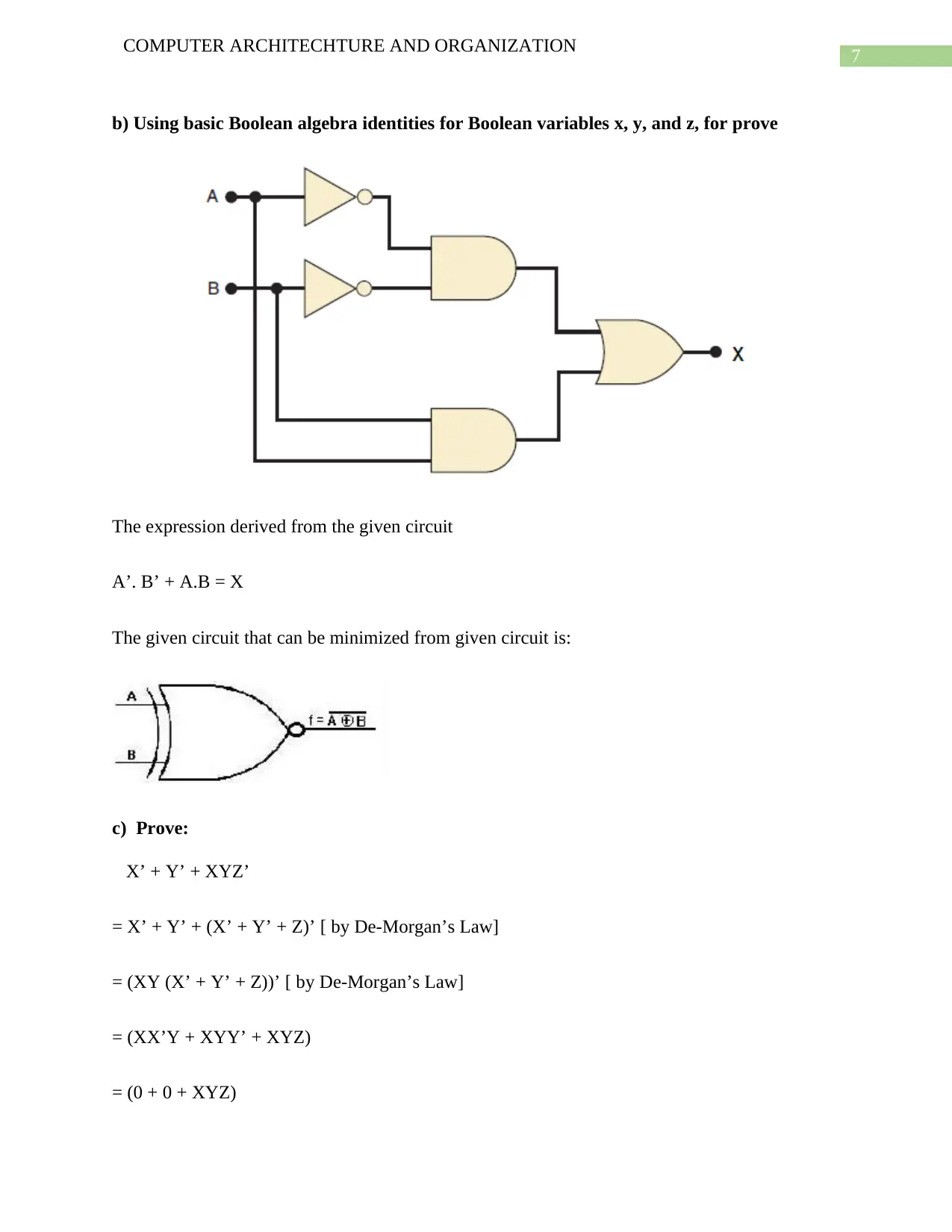
b) Using basic Boolean algebra identities for Boolean variables x, y, and z, for prove
The expression derived from the given circuit
A’. B’ + A.B = X
The given circuit that can be minimized from given circuit is:
c) Prove:
X’ + Y’ + XYZ’
= X’ + Y’ + (X’ + Y’ + Z)’ [ by De-Morgan’s Law]
= (XY (X’ + Y’ + Z))’ [ by De-Morgan’s Law]
= (XX’Y + XYY’ + XYZ)
= (0 + 0 + XYZ)
COMPUTER ARCHITECHTURE AND ORGANIZATION
b) Using basic Boolean algebra identities for Boolean variables x, y, and z, for prove
The expression derived from the given circuit
A’. B’ + A.B = X
The given circuit that can be minimized from given circuit is:
c) Prove:
X’ + Y’ + XYZ’
= X’ + Y’ + (X’ + Y’ + Z)’ [ by De-Morgan’s Law]
= (XY (X’ + Y’ + Z))’ [ by De-Morgan’s Law]
= (XX’Y + XYY’ + XYZ)
= (0 + 0 + XYZ)

8
COMPUTER ARCHITECHTURE AND ORGANIZATION
= (XYZ)’
= X’ + Y’ + Z’ [ by De-Morgan’s Law]
Hence, X’ + Y’ + XYZ’ = X’ + Y’ + Z’ [PROVED]
COMPUTER ARCHITECHTURE AND ORGANIZATION
= (XYZ)’
= X’ + Y’ + Z’ [ by De-Morgan’s Law]
Hence, X’ + Y’ + XYZ’ = X’ + Y’ + Z’ [PROVED]
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 9
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.


