Spring 2018 MAII3007 Numeracy 2: Complete Coursework Portfolio

This Numeracy 2 (MAII3007) coursework portfolio from Spring 2018 covers a range of financial numeracy topics. The portfolio includes calculations and explanations related to powers, roots, logarithms, simple and compound interest, linear relationships, net present value, data presentation using histograms, and probability. The solution demonstrates the application of these concepts through worked examples, including investment scenarios and data analysis. Skills audits are also included to evaluate progress. The portfolio also contains real life examples, online activities and reflective logs.

Student Name:
Student ID Number:
Tutor name:
This is your Numeracy 2 e-portfolio which you must submit by Wednesday 25th
April 2018 via the Student Portal.
Please read this carefully
Numeracy 2 (MAII3007) Coursework Portfolio
February 2018

This is your Numeracy 2 e-portfolio for the semester commencing February 2018 (Spring 2018). Please
save a copy on your computer and back it up regularly (e.g. by saving it on your computer / in the cloud
(e.g. Google Drive) / emailing it to yourself. You should print a working copy and bring it to all lectures
and tutorials. However, at the end of the course, you will need to submit a completed electronic copy.
Please read carefully the module handbook, the marking criteria and the grade descriptors.
Academic Misconduct
You are responsible for ensuring you understand the policy and regulations about academic
misconduct. You must:
• Complete this work alone except where required or allowed by this assignment briefing paper and
ensure it has not been written or composed by or with the assistance of any other person.
• Make sure all sentences or passages quoted from other people’s work in this assignment (with or
without trivial changes) are in quotation marks, and are specifically acknowledged by reference to
the author, work and page.
This portfolio consists of two sections:
Section 1is worth 75% of the final mark and consists of 8 questions (70%) and periodic Skills
Audit (carrying 5%).
Section 2consists of 3 tasks. Combined they are worth 25% of the final mark.
Task 1 – Two Real life examples (8%)
Task 2 – Online Activity (10%)
Task 3 – Reflective log (7%)

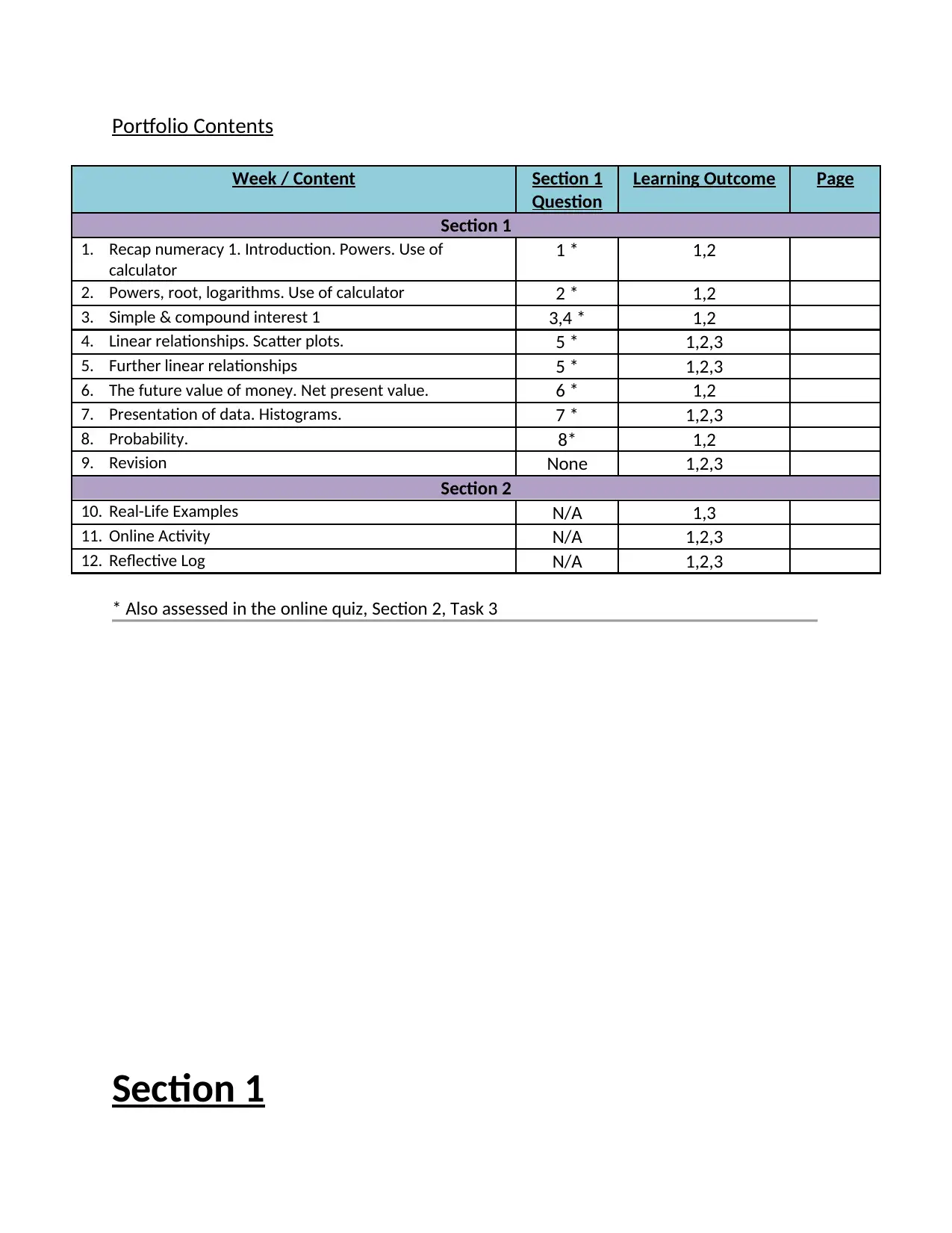
Portfolio Contents
Week / Content Section 1
Question
Learning Outcome Page
Section 1
1. Recap numeracy 1. Introduction. Powers. Use of
calculator
1 * 1,2
2. Powers, root, logarithms. Use of calculator 2 * 1,2
3. Simple & compound interest 1 3,4 * 1,2
4. Linear relationships. Scatter plots. 5 * 1,2,3
5. Further linear relationships 5 * 1,2,3
6. The future value of money. Net present value. 6 * 1,2
7. Presentation of data. Histograms. 7 * 1,2,3
8. Probability. 8* 1,2
9. Revision None 1,2,3
Section 2
10. Real-Life Examples N/A 1,3
11. Online Activity N/A 1,2,3
12. Reflective Log N/A 1,2,3
* Also assessed in the online quiz, Section 2, Task 3
Section 1

This section should be filled in as you acquire the skills required for each question.
Answer all questions. Please show your workings and/or explain your results as required.
Marks will be awarded for good presentation. Please evaluate your progress using the skills
audits provided.
You may use your calculator as required.
You must show your working.
QUESTION 1 [6 marks]
Powers and Roots:
a) Simplify 75 x 72(2 marks)
b) Simplify 103 ÷102 (2 marks)
c) Evaluate ( 123 )4 (2 marks)
[TYPE YOUR ANSWER HERE]
a) 75×73 = 75+3 = 78 .
b) 103 ÷ 102 = 101 = 10
c) (123)4= 1212

QUESTION 2 [8 marks]
a) Express the power 100 1/2using the root notation and evaluate. (2 marks)
b) Evaluate 3
√ 1,000,000 (2 marks)
c) Simplify 7 3
√ 8−4 3
√ 8 (2 marks)
d) Scientific notation allows one to express large or small numbers in a simpler form.
Express the UK population of 65,648,000 in a scientific notation (2 marks)
[TYPE YOUR ANSWER TO QUESTION 2 HERE]
a. 1001/2 = √100= 10
b. 3√1000000= 106/3 = 102 = 100
c. 73√8 - 43√8 = 7*2 - 4*2 =14-8 = 6
d. 65,648,000= 65.648 million

SKILLS AUDIT: WEEKS 1 – 2
I know how to…. I can do
well
I need
practice
I’m not
sure
I can’t
do
13. I understand what a power is ☐ ☐ ☐ ☐
14. I can perform calculations and
simplifications using power
☐ ☐ ☐ ☐
15. I understand what a root is ☐ ☐ ☐ ☐
16. I can perform calculations and
simplifications using roots, using a scientific
or financial calculator if required
☐ ☐ ☐ ☐
QUESTION 3 [10 marks]
Ann Miller invests £150,000 at an interest rate of 6% p.a.
Calculate the final balance after 5 years.
a) Using simple interest? (1 mark)
b) Using interest compounded annually? (3 marks)
c) Using interest compounded semi-annually? (3 marks)
d) Using interest compounded quarterly? (3 marks)
[TYPE YOUR ANSWER TO QUESTION 3 HERE]
Given Principal (P) = £150,000, Rate of Interest (R)= 6% p.a., Time (T)= 5 years
a. Simple Interest = P*R*T = £(150,000*6*5)/100 = £4500000/100=£45,000
b. (Interest being compounded annually)= P(1+R/N)NT =150,000(1+0.06/1)1*5
=£150000*1.338226= £200733.8
c. (Interest being compounded semi-annually) = P(1+R/N)NT =150,000(1+0.06/2)5*2
=£150000*1.343916 = £201587.5
d. Compound Interest= P(1+R/N)NT =150,000(1+0.06/4)5*4 = £150000*1.346855=£202028.

QUESTION 4 [10 marks]
a) Eliza invests £22,000 at a 2% interest rate annually.
Compounding the interest annually, how long will it take her
to receive the balance of £33,000?
(4 marks)
b)Using Rule 72, calculate how long will it take Eliza to double her investments?
(2 marks)
c) Mr Ramsbottom invests £32,000 in a bank savings account and after 10 years his
balance is £45,200.20.
Calculate the compound interest rate he received and round your answer to the
second decimal place.
(4 marks)
[TYPE YOUR ANSWER TO QUESTION 4 HERE]
Principal (P)= £22,000, Rate of Interest (R)= 2% pa, Rate of Interest compounded annually.
a. Needed time= log ( FV
PV )
log (1+r )=
log( 33000
22000 )
log(1+0.02)= log (3 /2)
log(1.02)= 0.176091
0.0086 =20.47. So time = 20
years
b. Year required= 72/2=36 years
c. Principal (P)= £32,000, Time (T)=10, Amount Received= £45,200.20
Rate of Interest equation:
45,200.20= 32000(1+r)10 ;
=) (1+r)10 = 1.412506;
=) (1+r) = (1.412506)(1/10) = 1.03;
=) r = 1.03-1 = 0.03;
=) r= 3%

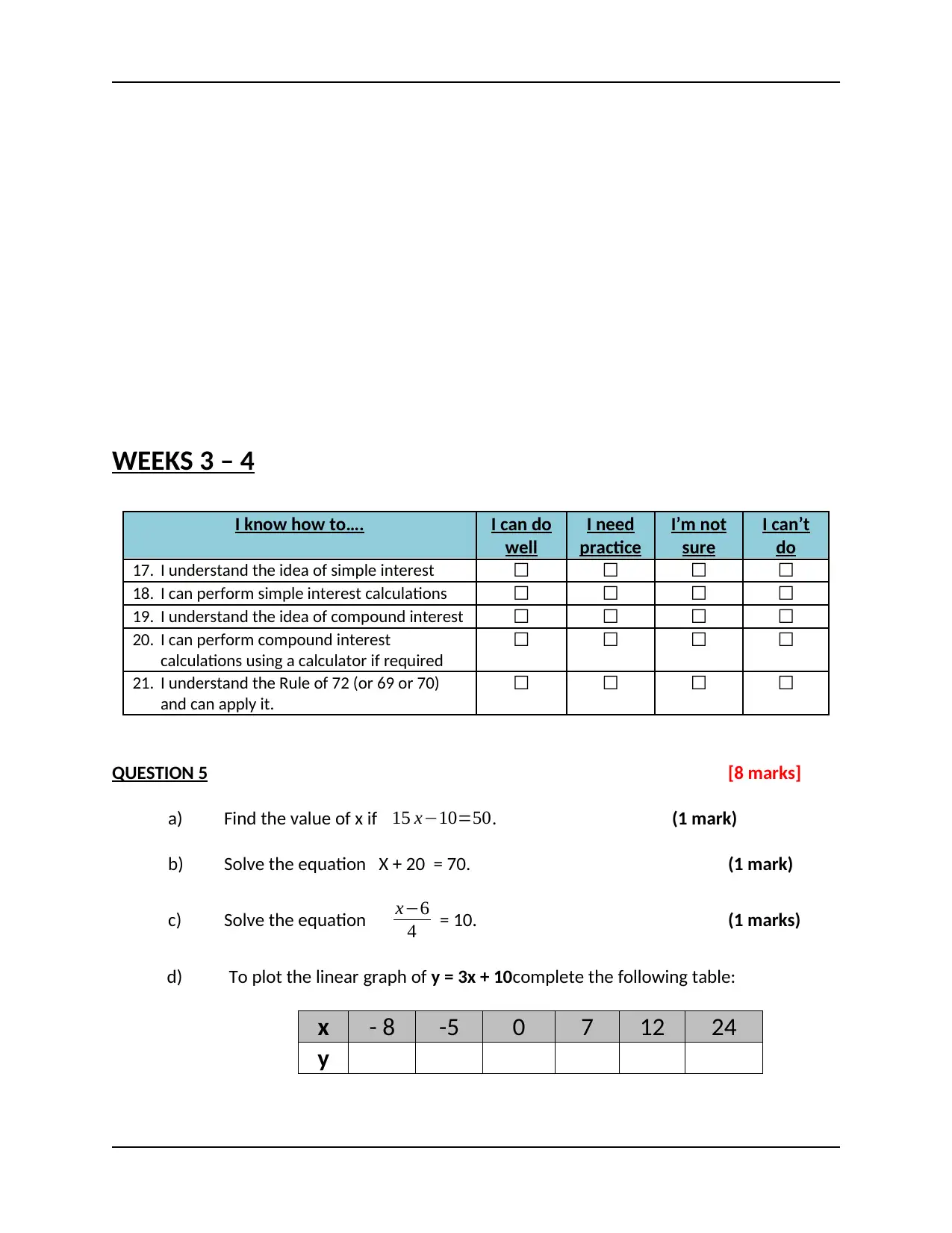
WEEKS 3 – 4
I know how to…. I can do
well
I need
practice
I’m not
sure
I can’t
do
17. I understand the idea of simple interest ☐ ☐ ☐ ☐
18. I can perform simple interest calculations ☐ ☐ ☐ ☐
19. I understand the idea of compound interest ☐ ☐ ☐ ☐
20. I can perform compound interest
calculations using a calculator if required
☐ ☐ ☐ ☐
21. I understand the Rule of 72 (or 69 or 70)
and can apply it.
☐ ☐ ☐ ☐
QUESTION 5 [8 marks]
a) Find the value of x if 15 x−10=50. (1 mark)
b) Solve the equation X + 20 = 70. (1 mark)
c) Solve the equation x−6
4 = 10. (1 marks)
d) To plot the linear graph of y = 3x + 10complete the following table:
x - 8 -5 0 7 12 24
y

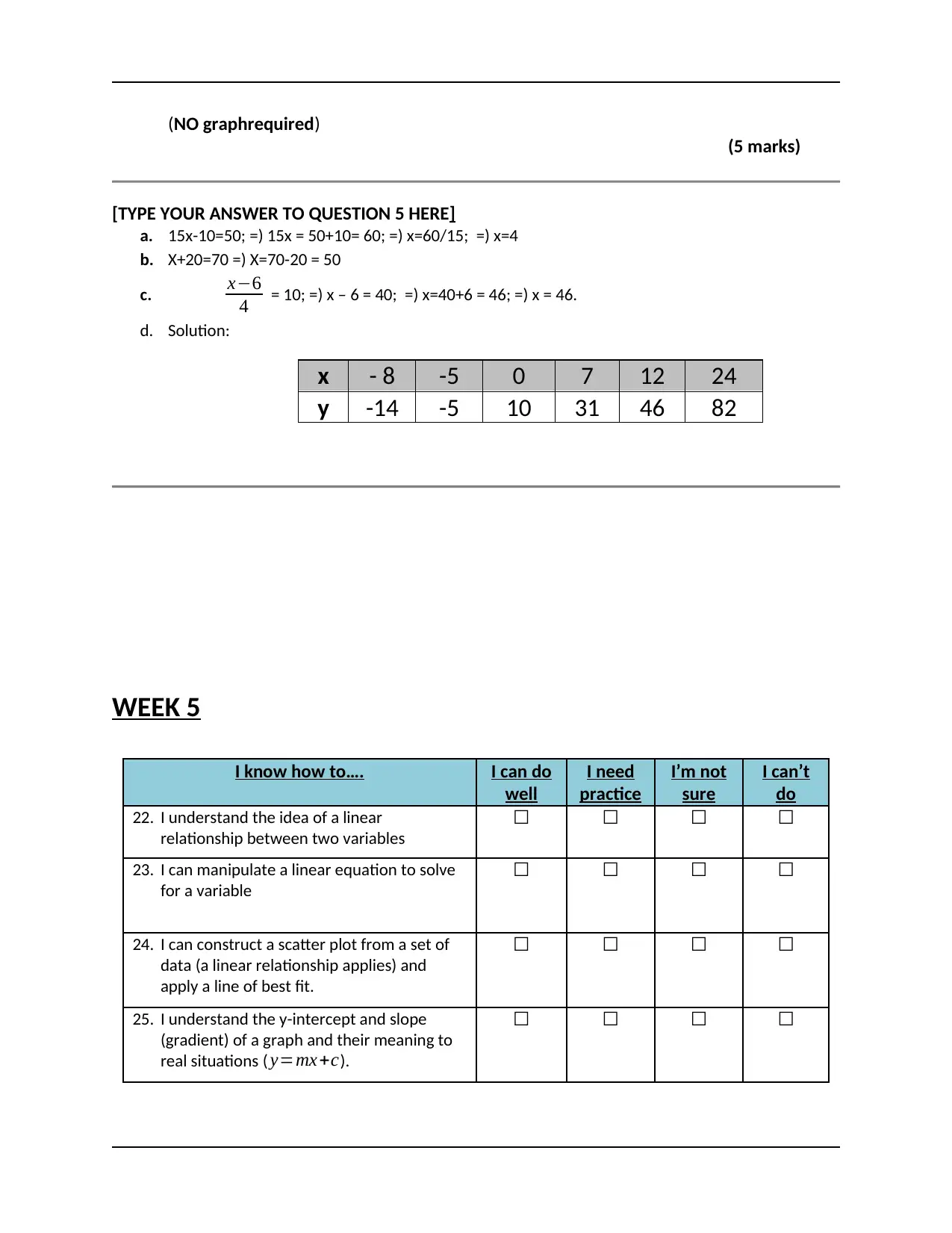
(NO graphrequired)
(5 marks)
[TYPE YOUR ANSWER TO QUESTION 5 HERE]
a. 15x-10=50; =) 15x = 50+10= 60; =) x=60/15; =) x=4
b. X+20=70 =) X=70-20 = 50
c. x−6
4 = 10; =) x – 6 = 40; =) x=40+6 = 46; =) x = 46.
d. Solution:
x - 8 -5 0 7 12 24
y -14 -5 10 31 46 82
WEEK 5
I know how to…. I can do
well
I need
practice
I’m not
sure
I can’t
do
22. I understand the idea of a linear
relationship between two variables
☐ ☐ ☐ ☐
23. I can manipulate a linear equation to solve
for a variable
☐ ☐ ☐ ☐
24. I can construct a scatter plot from a set of
data (a linear relationship applies) and
apply a line of best fit.
☐ ☐ ☐ ☐
25. I understand the y-intercept and slope
(gradient) of a graph and their meaning to
real situations ( y=mx+c).
☐ ☐ ☐ ☐

26. I can use the scatter plot produced in part
(12) to derive a linear relationship between
two variables ( y=mx+c).
☐ ☐ ☐ ☐
27. I can use the relationship from part (14) to
extrapolate and interpolate
☐ ☐ ☐ ☐

Question 6 [10 marks]
Sarah Hair Saloon is considering an investment project to purchase and run a Hair Saloon
business. The initial cost is £55,000. The annual cash inflows (income) are projected to be as
follows:
Year 1 Year 2 Year 3 Year 4
£15,000 £25,000 £45,000 £15,000
The discount rate for this investment is 8% p.a., compounded annually.
a) Work out the Net Present Value (NPV) of this investment. (8 marks)
b) Should Sarah proceed with this project?
Explain your reasoning. (2 marks)
[TYPE YOUR ANSWER TO QUESTION 6 HERE]
a. Initial Cost= £55,000,
Annual Cash Flow=
Year 1 Year 2 Year 3 Year 4
£15,000 £25,000 £45,000 £15,000
Rate of Interest=8%
NPV= ∑
t =1
T Ct
( 1+ r)t - C0
=(15000/(1+0.08)) + (25000/(1+0.08)2) + (45000/(1+0.08)3) + (15000/(1+0.08)4) – 55000
=£(16200+29160+56687.04+20407.33-55000)
=£(122454.4 – 55000) = £67454.37.
b. Net Present value is the difference between the present value of cash inflow and present value
of cash outflow. A positive NPV would imply acceptation of the investment and negative NPV
would imply rejection. Since the value is quite high and positive. Hence, Sarah should proceed
with the investment. However, there is no option for comparison here, since no alternative NPV
value is available.
WEEK 6