Numeracy 2 (MAII3007) Coursework Portfolio, Spring 2018, University

This Numeracy 2 portfolio assignment, submitted in April 2018, covers a range of financial and mathematical concepts. Section 1 includes detailed solutions and explanations for questions on powers, roots, simple and compound interest calculations, linear relationships, net present value, histograms, and probability. The portfolio demonstrates the application of these concepts through calculations and problem-solving. Section 2 requires the student to provide real-life examples related to the module's topics. The assignment also includes skills audits to self-assess understanding of the concepts. The student demonstrates proficiency in calculating powers, roots, interest (simple and compound), solving linear equations, working with NPV, creating histograms, and calculating probabilities.

Student Name:
Student ID Number:
Tutor name:
This is your Numeracy 2 e-portfolio which you must submit by Wednesday
25th April 2018 via the Student Portal.
Please read this carefully
Numeracy 2 (MAII3007) Coursework Portfolio
February 2018

This is your Numeracy 2 e-portfolio for the semester commencing February 2018 (Spring 2018). Please
save a copy on your computer and back it up regularly (e.g. by saving it on your computer / in the cloud
(e.g. Google Drive) / emailing it to yourself. You should print a working copy and bring it to all lectures
and tutorials. However, at the end of the course, you will need to submit a completed electronic copy.
Please read carefully the module handbook, the marking criteria and the grade descriptors.
Academic Misconduct
You are responsible for ensuring you understand the policy and regulations about academic
misconduct. You must:
• Complete this work alone except where required or allowed by this assignment briefing paper and
ensure it has not been written or composed by or with the assistance of any other person.
• Make sure all sentences or passages quoted from other people’s work in this assignment (with or
without trivial changes) are in quotation marks, and are specifically acknowledged by reference to the
author, work and page.
Portfolio Contents
Week / Content Section 1
Question
Learning Outcome Page
Section 1
1. Recap numeracy 1. Introduction. Powers. Use of
calculator
1 * 1,2
2. Powers, root, logarithms. Use of calculator 2 * 1,2
3. Simple & compound interest 1 3,4 * 1,2
4. Linear relationships. Scatter plots. 5 * 1,2,3
5. Further linear relationships 5 * 1,2,3
6. The future value of money. Net present value. 6 * 1,2
7. Presentation of data. Histograms. 7 * 1,2,3
8. Probability. 8* 1,2
9. Revision None 1,2,3
Section 2
10. Real-Life Examples N/A 1,3
11. Online Activity N/A 1,2,3
12. Reflective Log N/A 1,2,3

* Also assessed in the online quiz, Section 2, Task 3
Section 1
This section should be filled in as you acquire the skills required for each question.
Answer all questions. Please show your workings and/or explain your results as required.
Marks will be awarded for good presentation. Please evaluate your progress using the skills
audits provided.
You may use your calculator as required.
You must show your working.
QUESTION 1 [6 marks]
Powers and Roots:
a) Simplify 75 x 72 (2 marks)
using the indices rule, we add the power when there is multiplication
= 75 +2=77
= 823543
b) Simplify 103 ÷102 (2 marks)
when there is division, we subtract the powers using the rule of indices.
= 103−2=101 = 10
c) Evaluate ( 123 )4 (2 marks)
In this case, the powers are multiplied as they are within a bracket.
= 123 ×4 =1212 = 8916100448256
[TYPE YOUR ANSWER HERE]

QUESTION 2 [8
marks]
a) Express the power 100 1/2 using the root notation and evaluate. (2 marks)
10 0
1
2 =¿ √ 100
= √10 ×10=10
b) Evaluate 3
√ 1,000,000 (2
marks)
c) Simplify 7 3
√ 8−4 3
√ 8 (2
marks)
7 3
√ 8−4 3
√ 8=7 3
√ 23 −4 3
√ 23
= 7 ×2−4 × 2 = 14 – 8
= 6
d) Scientific notation allows one to express large or small numbers in a simpler form.
Express the UK population of 65,648,000 in a scientific notation (2 marks)
This can be represented in scientific notation as 6.5648 ×107
[TYPE YOUR ANSWER TO QUESTION 2 HERE]

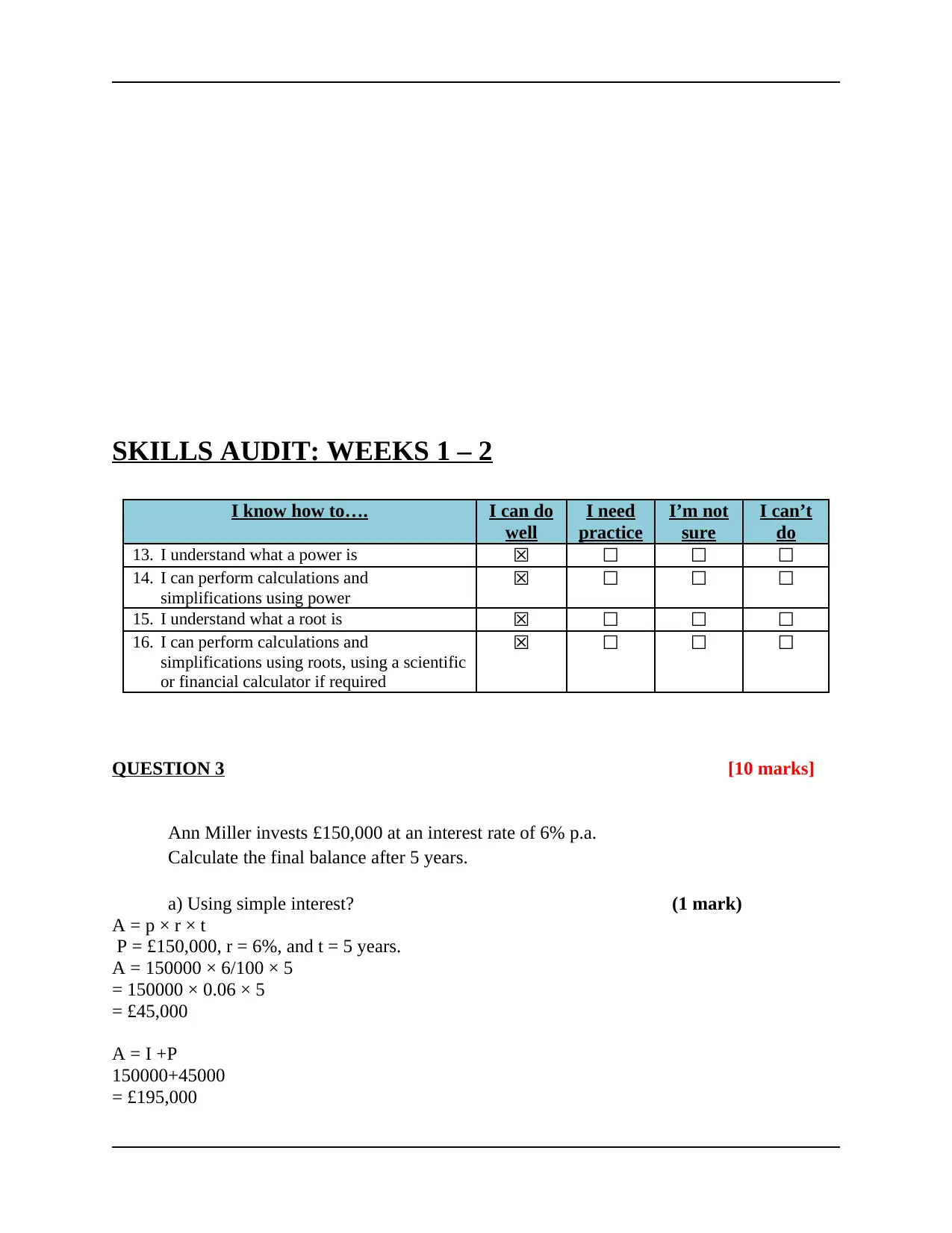
SKILLS AUDIT: WEEKS 1 – 2
I know how to…. I can do
well
I need
practice
I’m not
sure
I can’t
do
13. I understand what a power is ☒ ☐ ☐ ☐
14. I can perform calculations and
simplifications using power
☒ ☐ ☐ ☐
15. I understand what a root is ☒ ☐ ☐ ☐
16. I can perform calculations and
simplifications using roots, using a scientific
or financial calculator if required
☒ ☐ ☐ ☐
QUESTION 3 [10 marks]
Ann Miller invests £150,000 at an interest rate of 6% p.a.
Calculate the final balance after 5 years.
a) Using simple interest? (1 mark)
A = p × r × t
P = £150,000, r = 6%, and t = 5 years.
A = 150000 × 6/100 × 5
= 150000 × 0.06 × 5
= £45,000
A = I +P
150000+45000
= £195,000

b) Using interest compounded annually? (3 marks)
A = P (1 + r)t
= 150000(1+0.06)5
= 150000(1.06)5
= £ 200733.8 4
c) Using interest compounded semi-annually? (3 marks)
A = P (1 + r/n)t, t = 2
= 150000(1+0.06/2)5×2
= 150000(1.03)10
= £ 201587.46
d) Using interest compounded quarterly? (3 marks)
A = P (1 + r/n)t, t = 2
= 150000(1+0.06/4)5×4
= 150000(1.015)20
= 202028.25098250841
[TYPE YOUR ANSWER TO QUESTION 3 HERE]

QUESTION 4 [10
marks]
a) Eliza invests £22,000 at a 2% interest rate annually.
Compounding the interest annually, how long will it take her
to receive the balance of £33,000?
(4 marks)
A = P (1 + r)t,
33000=22000(1+0.02)t
t=log1.02 ( 3
2 )
t = 20.4753188576339 years
I will take approximately 20.5 years for the amount to be £33,000
b) Using Rule 72, calculate how long will it take Eliza to double her investments?
(2 marks)
The time required for the amount to double is;
= 72/r
72/2 = 36years
c) Mr Ramsbottom invests £32,000 in a bank savings account and after 10 years his
balance is £45,200.20.
Calculate the compound interest rate he received and round your answer to the
second decimal place.
(4 marks)
A = P (1 + r)t,
45200.20 = 32000(1+r)10
1.41250625 = (1+r)10
1 + r = 10
√ 1.41250625 = 1.0351398733097
r = 0.03514
r = 3.514%
[TYPE YOUR ANSWER TO QUESTION 4 HERE]

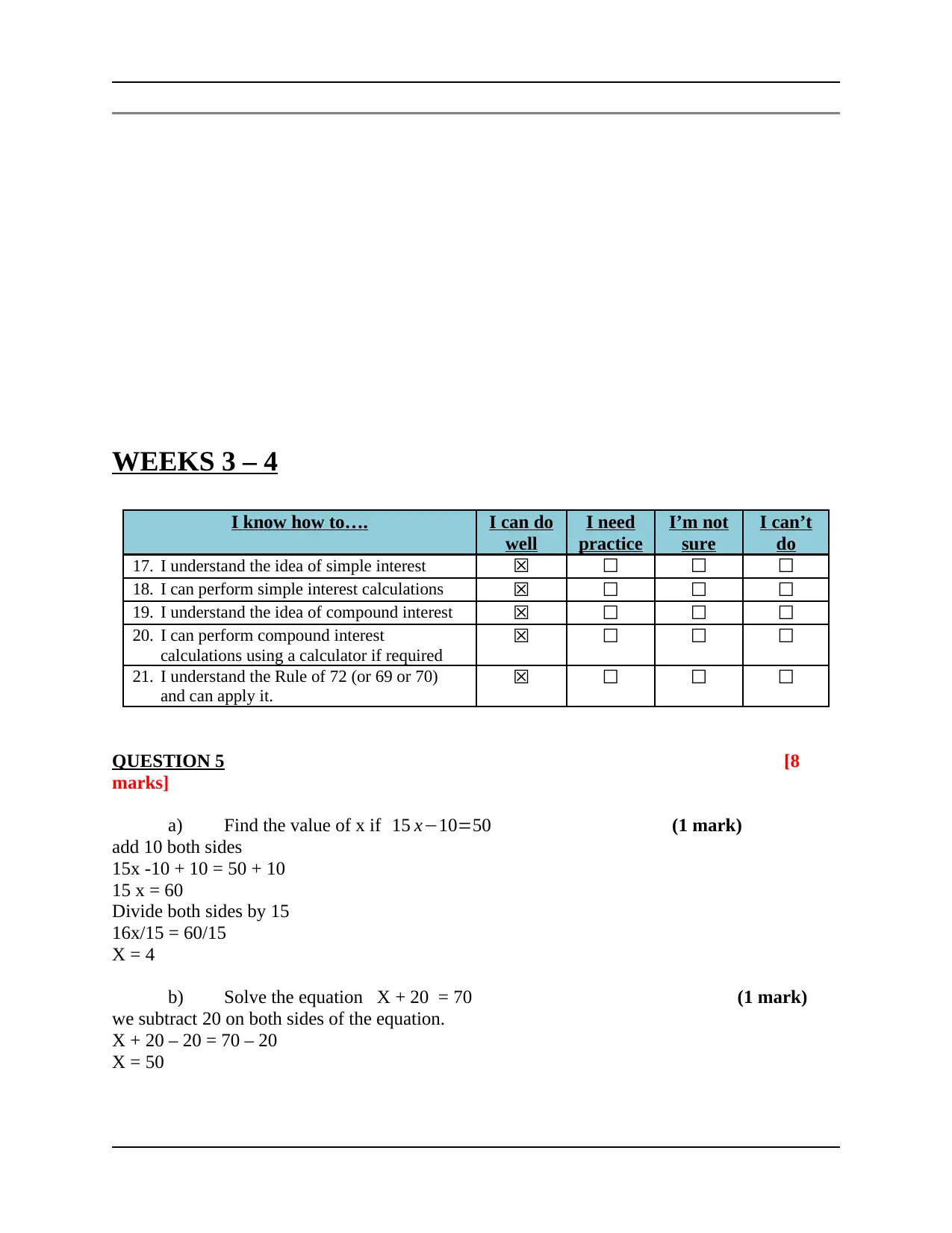
WEEKS 3 – 4
I know how to…. I can do
well
I need
practice
I’m not
sure
I can’t
do
17. I understand the idea of simple interest ☒ ☐ ☐ ☐
18. I can perform simple interest calculations ☒ ☐ ☐ ☐
19. I understand the idea of compound interest ☒ ☐ ☐ ☐
20. I can perform compound interest
calculations using a calculator if required
☒ ☐ ☐ ☐
21. I understand the Rule of 72 (or 69 or 70)
and can apply it.
☒ ☐ ☐ ☐
QUESTION 5 [8
marks]
a) Find the value of x if 15 x−10=50 (1 mark)
add 10 both sides
15x -10 + 10 = 50 + 10
15 x = 60
Divide both sides by 15
16x/15 = 60/15
X = 4
b) Solve the equation X + 20 = 70 (1 mark)
we subtract 20 on both sides of the equation.
X + 20 – 20 = 70 – 20
X = 50

c) Solve the equation x−6
4 = 10 (1
marks)
d) To plot the linear graph of y = 3x + 10 complete the following table:
x - 8 -5 0 7 12 24
y -14 -5 10 31 46 82
(NO graph required)
(5
marks)
[TYPE YOUR ANSWER TO QUESTION 5 HERE]
WEEK 5
I know how to…. I can do
well
I need
practice
I’m not
sure
I can’t
do
22. I understand the idea of a linear relationship
between two variables
☒ ☐ ☐ ☐
23. I can manipulate a linear equation to solve
for a variable
☒ ☐ ☐ ☐
24. I can construct a scatter plot from a set of
data (a linear relationship applies) and apply
a line of best fit.
☒ ☐ ☐ ☐
25. I understand the y-intercept and slope
(gradient) of a graph and their meaning to
real situations ( y=mx+c).
☒ ☐ ☐ ☐

26. I can use the scatter plot produced in part
(12) to derive a linear relationship between
two variables ( y=mx+c).
☒ ☐ ☐ ☐
27. I can use the relationship from part (14) to
extrapolate and interpolate
☒ ☐ ☐ ☐

Question 6 [10 marks]
Sarah Hair Saloon is considering an investment project to purchase and run a Hair Saloon
business. The initial cost is £55,000. The annual cash inflows (income) are projected to be as
follows:
Year 1 Year 2 Year 3 Year 4
£15,000 £25,000 £45,000 £15,000
The discount rate for this investment is 8% p.a., compounded annually.
a) Work out the Net Present Value (NPV) of this investment. (8 marks)
NPV = (C for Period 1 / (1 + R)1) + (C for Period 2 / (1 + R)2) ... (C for Period x / (1 + R)x) -
Initial Investment
= (15000/(1+0.08)1 + (25000/(1+0.08)2 + (45000/(1+0.08)3 + (15000/(1+0.08)4 – 55000
= £ 27070.2 6
b) Should Sarah proceed with this project?
Explain your reasoning. (2 marks)
Sara should proceed with the investment. This is because the Net present value of the investment
is more that the initial invested amount. In other words, the net worth is positive.
[TYPE YOUR ANSWER TO QUESTION 6 HERE]
WEEK 6
I know how to…. I can do
well
I need
practice
I’m not
sure
I can’t
do
28. I understand the idea of the future value of
money
☒ ☐ ☐ ☐

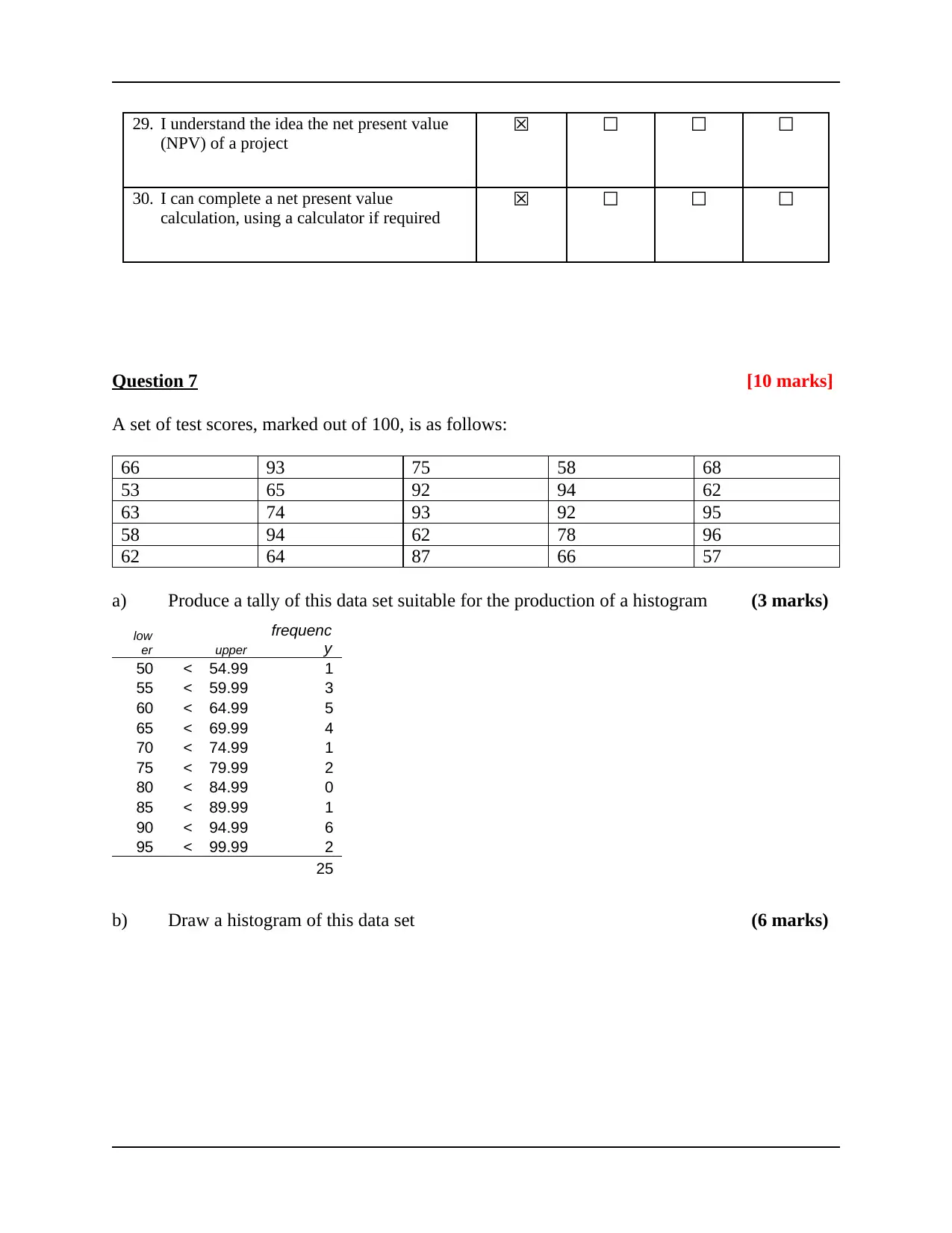
29. I understand the idea the net present value
(NPV) of a project
☒ ☐ ☐ ☐
30. I can complete a net present value
calculation, using a calculator if required
☒ ☐ ☐ ☐
Question 7 [10 marks]
A set of test scores, marked out of 100, is as follows:
66 93 75 58 68
53 65 92 94 62
63 74 93 92 95
58 94 62 78 96
62 64 87 66 57
a) Produce a tally of this data set suitable for the production of a histogram (3 marks)
low
er upper
frequenc
y
50 < 54.99 1
55 < 59.99 3
60 < 64.99 5
65 < 69.99 4
70 < 74.99 1
75 < 79.99 2
80 < 84.99 0
85 < 89.99 1
90 < 94.99 6
95 < 99.99 2
25
b) Draw a histogram of this data set (6 marks)

c) Comment on the distribution of these marks. (1 marks)
the chart shows that there are fewer observations on the upper side of the chart which deviate
from other data points. Thus, in this case, it means that the data have a relative longer tail to the
right. Thus, it can be concluded that the data are positively skewed.
[TYPE YOUR ANSWER TO QUESTION 7 HERE]
WEEK 7
I know how to…. I can do
well
I need
practice
I’m not
sure
I can’t
do
31. I understand the idea of frequency
distribution
☒ ☐ ☐ ☐

32. I can read and interpret a histogram ☒ ☐ ☐ ☐
33. I can construct a histogram from a set of
data
☒ ☐ ☐ ☐
Question 8 [8 marks]
Probability is a measure of the likelihood and can be stated as a ratio, percentage or generally as
a number between zero and one.
a) What is the probability when the likelihood is impossible? (1 mark)
the probability when the likelihood is impossible is zero. This means that out of all the possible
outcome, the one selected cannot happen.
b) What is the probability when the likelihood is certain? (1 mark)
The probability of a certain event is 1. In other words, there is 100% certainty that an event will
occur. However, these events are rare. S
c) Express the probability of 0.06 as a % (2 marks)
to convert a decimal number to a percentage, we just need to multiply that number by 100.
0.06 × 100 = 6%
d) Josiah tossed a coin and thrown a die at the same time (simultaneously). Work out the
probability of getting a head on the coin and a 5 on the die.
(4 marks)
In this case, the sample space is: {H1, H2, H3, H4, H, 5, H6, T1, T2, T3, T4, T5, T6}
Thus, there is only one chance out of 12 of getting a head on the coin and a 5 on the die.
The probability is, therefore, 1
12
[TYPE YOUR ANSWER TO QUESTION 8 HERE]

WEEK 8
I know how to…. I can do
well
I need
practice
I’m not
sure
I can’t
do
34. I understand simple probabilities ☒ ☐ ☐ ☐
35. I can perform probability calculations, using
a calculator if required
☒ ☐ ☐ ☐
36. I understand and can perform exchange rate
calculations
☒ ☐ ☐ ☐

Section 2
Task 1 - Two Real life examples (100 words each) [8
marks]
Give two real-life situations or problems in businesses that involve the topics studied in
this module (e.g. powers and roots, simple and compound interests, linear relationships,
graphs, probabilities and Net Present values (NPV)).
[TYPE YOUR ANSWERS TO TASK 1 HERE]
(1) (4 marks)
First, application of mathematics in real life is almost in each aspect. Compound
interest rate is the most pronoun form of interest in which the interest rate is earned
on a cumulative basis. This is mostly used to calculate the interest rates of loans, as
they yield a higher revenue on loans as compared to the simple interest rate. A good
example is a case where the interest rate is 10% and one borrows £10,000 for a
period of two years. The interest earned in first years will be A=£ 10000 ( 1+ 10
100 )
1
= 11000, the interest rate of the second-year amount will be calculated on this new
amount. Therefore, loans are given on the basis of compound interest.
Graphs have a lot of uses in real life. First, plots such as bar graph are used in
illustrating the trend of some factors over time. This is because they depict the trend
clearer. The longer the column in the plot the higher the value associated with that
category. Also, a plot such as scatter plot are used to determine whether two factors of
variables are associated. The plot shows the strength and direction of the association. A
good example is trying to understand the behaviour of sales using the amount invested
on the advertisement. One can plot a scatter plot using sales as the dependent variable
and advertising amount as the independent variable. The plot is used to determine
whether there is a plausible relationship between the two variables.
(2) (4 marks)
Task 2 - Online Activities [10 marks]
This relates to the quiz. Please complete and pass all three relevant quiz/activity;
screenshot and save the result’s screen ready to be pasted on the portfolio.
Ensure the followings are visible before the screenshot:
 Your full names on the top right-hand corner of the screen

 Your test result is any score from 40% to 100%
[PASTE YOUR SCREENSHOTS FOR TASK 2 HERE]
Task 3 - Reflective Log (150 words) [7
marks]
This reflective log should develop as the course proceeds, and may be the last part to be
completed. Reflect honestly on your experiences throughout the semester. Start your
reflective log from week one by completing the skills audits and by writing personal
weekly notes after each topic. Please ask for your Tutor’s support if needed.
You may wish to consider the following points when providing your reflective
comments:
 Which topics do you feel most confident about? (e.g. powers and roots, interest rates,
NPV etc.)
 Are there areas for improvement (e.g. in probability, I need do practice more or research
etc.)?
 How would you evaluate your participation on the module (e.g. contribution to classes,
independent study etc.)?
[I have confidence in square root, solving equations and indices. Those I except the
get quite good grade. Working with powers was quite interesting although I had
some issues initially especially when working with either division of multiplication
of numbers with equal base but different powers. In particular, understanding that
when one is doing division, the powers should be subtracted, and when multiplying
the powers should be added. However, I would like some improvement in the
future values of investment and compound interest especially those that are
computed either monthly or continuously. I have come across such a problem and
finding the interest rate was quite hectic. Although this can be improved over time,
I will try and do lots or research and practice on these areas. I had a lot of
headache understanding those concepts. My contribution was quite well in class
and discussions, and I did all the test with high integrity.]