University Data Analysis and Numeracy Assignment: Rome Humidity Study

This assignment provides a detailed analysis of humidity data in Rome, Italy, collected over a ten-day period. It begins with representing the data in tabular form and then visualizes it using bar and column charts. The core of the assignment involves calculating key statistical measures including the mean, median, mode, range, and standard deviation of the humidity data. Furthermore, the assignment explores the relationship between the days and humidity to determine the values of 'm' and 'c' in a linear equation, enabling the forecasting of humidity levels for days 15 and 20. The solution demonstrates the application of these statistical methods to real-world data and concludes with a summary of the findings.

Numeracy
&
Data Analysis

Table of Contents
INTRODUCTION................................................................................................................................1
MAIN BODY.......................................................................................................................................1
1. Representation of data in tabular form:...................................................................................1
2. Dara representation in charts:..................................................................................................2
3. Calculations of mean, median, mode, standard deviation and range:.....................................3
4. Calculating values of m, c and wind forecast of day 15 and 20..............................................6
CONCLUSION....................................................................................................................................7
REFERENCES.....................................................................................................................................8

INTRODUCTION
The term data analysis can be described as a coordinated system for the collection and
analysis of financial information using a broad array of techniques (Landtblom, 2018). The
research focused on examining the humidity data of the city of Rome is selected which is
situated in Italy over the last ten days. This evaluation also includes a number of many other
calculations such as medium, mode, standard deviation etc. In addition the study also includes
the suitable experiment which is used to determine the value of m & c so that humidity forecasts
can be calculated for respective days.
MAIN BODY
1. Representation of data in tabular form:
The data describe below is collected to the context Rome relevant to humidity proportion
(%). The respective information is gathered between 28 Dec 2019 to 6 Jan 2020 (Humidity data
of rome, 2019).
Days (Date) Humidity (values in percentage-form)
28 of Dec., 2019 81%
29 of Dec., 2019 56%
30 of Dec., 2019 60%
31 of Dec., 2019 65%
1 of Jan, 2020 70%
2 of Jan, 2020 75%
3 of Jan, 2020 87%
4 of Jan, 2020 87%
5 of Jan, 2020 87%
6 of Jan, 2020 56%
2. Dara representation in charts:
Bar Graph: A bar diagram is needed to actually demonstrate information with bars in different
elevations or diameters. This substantially leads to some of the most effective assessment of the
collected data. Throughout this case, the data provided here is as tries to follow well into the
following style:
1

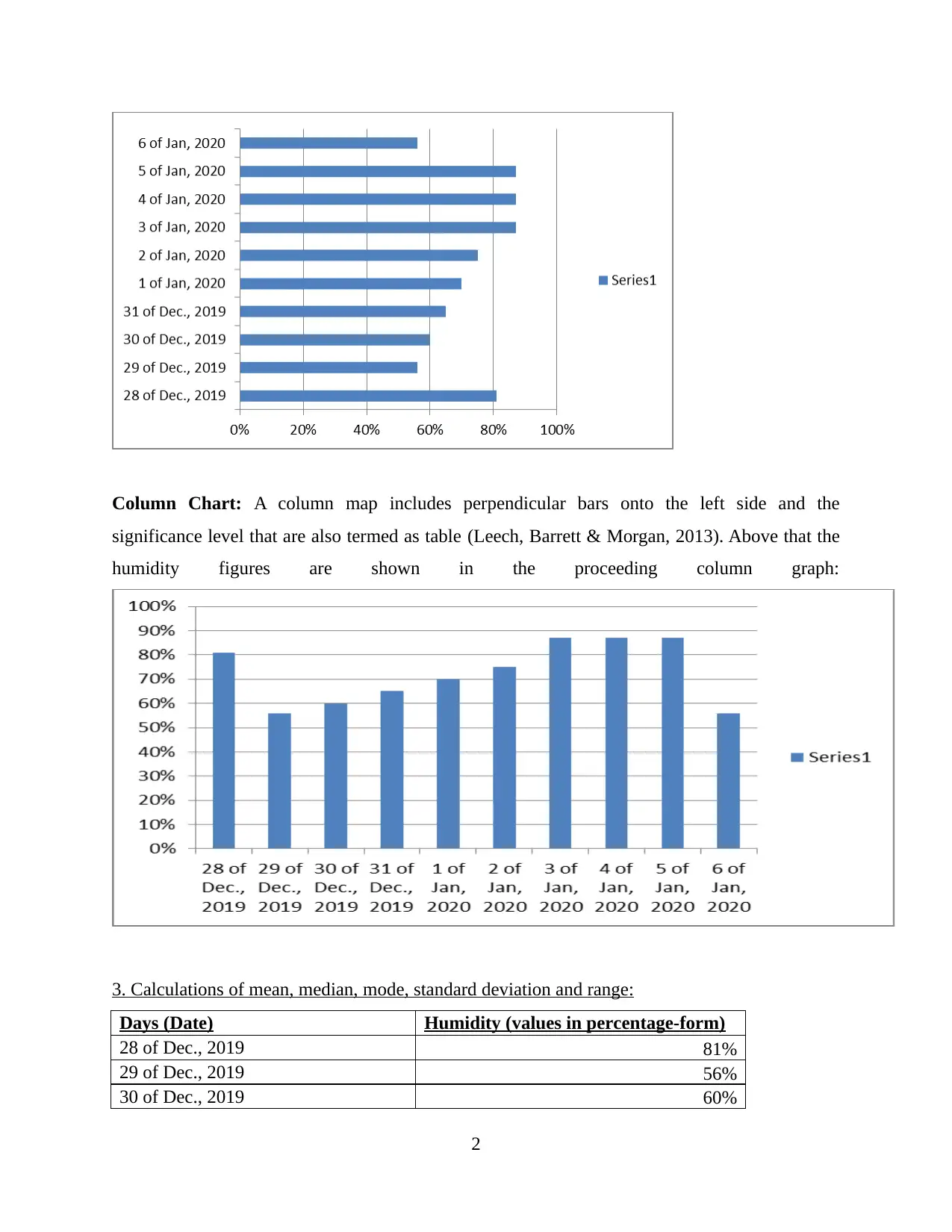
Column Chart: A column map includes perpendicular bars onto the left side and the
significance level that are also termed as table (Leech, Barrett & Morgan, 2013). Above that the
humidity figures are shown in the proceeding column graph:
3. Calculations of mean, median, mode, standard deviation and range:
Days (Date) Humidity (values in percentage-form)
28 of Dec., 2019 81%
29 of Dec., 2019 56%
30 of Dec., 2019 60%
2

31 of Dec., 2019 65%
1 of Jan, 2020 70%
2 of Jan, 2020 75%
3 of Jan, 2020 87%
4 of Jan, 2020 87%
5 of Jan, 2020 87%
6 of Jan, 2020 56%
∑ X 724
Mean 72.4
Median 72.2
Mode 87
Range 31
Maximum range 87
Minimum 56
Mean: Mean numerical details obtained can be defined on the basis of a specific calculation:
mean = ∑ N / N. The average amount is thus calculated in this situation:
N = 10
∑ N = 724
Mean= 724 / 10
= 72.4
Median = As the name it can be defined as a middle value of the temperature record. This is
calculated by a method based on the evidence about numbers. If number of data is odd then, M =
(N + 1 / 2)th item
If number of data is even then, M = {N/2th item+ N/2th item + 1}2
Herein, below calculation of median of humidity data is done below in such manner:
Humidity (in terms of %)
56
56
60
65
70
75
81
87
87
87
3

= {10/2+ 10/2 +1} / 2
= (5th item + 6th item) / 2
= (70+75) / 2
= 72.2
Mode- The term mode can be defined as a value set which appear primarily in a
quantitative range. As regards the above-mentioned humidity findings of Rome, 87% moisture
repeats 3 times thus the model value can be 87%.
Range- It is defined as a difference among highest possible and lowest values of the
given data set. In the context of the Rome humidity, the significant figure of 87 is higher and 56
are recorded to be the lowest. Therefore the size range is 87-56= 31
Standard deviation-- This seems to be a mathematical equation used for the assessment
of the average variances or diffusion. This is a measure of volatility of variety (Sarkar and
Rashid, 2016). Throughout this case, standard deviation measure is carried out as observes:
Days (Date)
Humidity (values in
%) x- m (x-m)2
Days (Date)
Humidity (values in
percentage-form)
28 of Dec., 2019 81 8.6 73.96
29 of Dec., 2019 56 -16.4 268.96
30 of Dec., 2019 60 -12.4 153.76
31 of Dec., 2019 65 -7.4 54.76
1 of Jan, 2020 70 -2.4 5.76
2 of Jan, 2020 75 2.6 6.76
3 of Jan, 2020 87 14.6 213.16
4 of Jan, 2020 87 14.6 213.16
5 of Jan, 2020 87 14.6 213.16
6 of Jan, 2020 56 -16.4 268.96
1472.4
Variance = [ ∑(x – mean) 2 / N ]
= (1472.4/10)
= 147.24
Standard deviation: √ ( variance )
= √ 147.24
4

= 12.13
4. Calculating values of m, c and wind forecast of day 15 and 20.
Form above computations summarised in table, following are the steps to find out the value of
“m” in equation which is y = mx + c as follows:
1. Compute value of m:
m = n (∑xy)- (∑x) (∑y)/ n(∑x2)-( ∑x)2
Days (Date)
Humidity (values in
%) x2 (xy)
Days (Date)
Humidity (values in
percentage-form)
1 81 1 81
2 56 4 112
3 60 9 180
4 65 16 260
5 70 25 350
6 75 36 450
7 87 49 609
8 87 64 696
9 87 81 783
10 56 100 560
55 724 385 4081
m = 10*4081-55*724 / 10*385-(55) 2
= 40810-39820/ 825
= 1.2
2. Computation of value of c: [(∑y) / n]-m(∑x/n)
= 724/10- 1.2(55/10)
= 72.4- 6.6
= 65.8
3. In accordance of above calculated data, forecasting of humidity is done below in such manner:
Forecast humidity for 15 day Y= mx+c
= 1.2*15+65.8
= 83.8%
5

Forecast humidity for 20 day Y= mx+c
= 1.2*20+65.8
= 89.8%
CONCLUSION
From the project study described above, data analysis was communicated that any
concrete findings from data series aggregation are too significant to quantify. In accordance with
the designated data set the research suggests on medium-mode estimates. The default deviation is
also calculated. The moisture content is measured between 15 and 20 days at the end of the test.
6

REFERENCES
Books and Journals:
Landtblom, K. K., 2018. Prospective Teachers’ Conceptions of the Concepts Mean, Median and
Mode. In Students' and Teachers' Values, Attitudes, Feelings and Beliefs in Mathematics
Classrooms (pp. 43-52). Springer, Cham.
Beyer, W. H., 2019. Handbook of tables for probability and statistics. Crc Press.
Sarkar, J. and Rashid, M., 2016. Visualizing mean, median, mean deviation, and standard
deviation of a set of numbers. The American Statistician. 70(3). pp.304-312.
Leech, N., Barrett, K. and Morgan, G. A., 2013. SPSS for intermediate statistics: Use and
interpretation. Routledge.
Online
Humidity data of London. 2019. [Online]. Available through:
<https://www.timeanddate.com/weather/uk/london/historic>
7