Numeracy, Data, and IT Assessment: Calculations and Analysis

This document provides a comprehensive solution to a Numeracy, Data, and IT assessment, covering a wide range of topics including basic calculations, percentage and fraction conversions, binary arithmetic, and spreadsheet applications. The assessment includes problems on calculating mean, mode, and standard deviation from given data sets, interpreting data from tables, and applying formulas within spreadsheets. The solution also demonstrates the use of charts and graphs for data representation, and discusses the application of filter functions. Additionally, the assessment tests the ability to solve practical problems involving discounts, payroll calculations, and analyzing expenditures, offering a detailed step-by-step approach to each problem.

Numeracy, Data and IT

Assessment Part 1
Section 1
Question 1
What is the result of following calculation?
I I I I I I I – I I I I
Solution: 8 – 4 = 4
i.e. I I I I
Question 2
What percentage of 70 does 49 equal to?
Solution: Let y% of 70 is 49
then, y% X 70 = 49
y/100 X 70 = 49
7/10 y = 49
y = 49 X 10/7
y = 70%
So, 70% of 70 is equal to 49. (Answer)
Question 3
Complete the following table to show equivalent fraction and percentage-
Fraction Percentage
45.00%
2.00/3.00
22.50%
7.00/5.00
Working notes:
(i)45% can be written in fraction form as -
1

45% = 45/100
in simplest form, divide both numerator and denominator by 5 then,
45% = 45 ÷ 5 / 100 ÷ 5
= 9/20 (Answer)
(ii) 2/3 can be converted into percentage form through multiply by 100 as -
2/3 X 100 = 66.66% approx. (Answer)
(iii) 22.50% can be written in fraction form as -
22.50% = 22.50/100
22.50% = 225 / 1000
in simplest form, divide both numerator and denominator by 25 then,
22.50% = 225 ÷ 25 / 1000 ÷ 25
= 9 / 40 (Answer)
(iv) 7/5 can be converted into percentage form through multiply by 100 as -
7/5 X 100 = 140% approx. (Answer)
So, the given has been completed as -
Fraction Percentage
9/20 45.00%
2/3 66.66%
9/40 22.50%
7/5 140.00%
b) A carton contains 150 cereal bars. What fraction of this number will each person get when
distributed to a class of 20 students?
Solutions: Total number of cereal bars – 150
Total number of students – 20
So, each student will get -
150 / 20 = 15 / 2 (answer).
Question 4:
Samuel paid cash for 3 discount-priced football tickets. He was given £4.20 change from the
three £50 notes he tendered. What was the price of each ticket?
2

Solution:
Total amount tendered by Samuel = 3 x £50 = £150
Changes received by Samuel = £4.20
No. of tickets = 3
So, changes get per ticket = 4.20 / 3 = £1.4
Therefore, price of each ticket after discount = 50 – 1.4 = £48.60
Question 5:
a) Solve this binary arithmetic: 10011 +10101
Solution: To sum of the given binary digit, firstly converted them into numbers by taking base 2
as -
100112 = 1 x 24 + 0 x 23 + 0 x 22 + 1 x 21 + 1 x 20
= 1 x 16 + 0 x 8 + 0 x 4 + 1 x 2 + 1 x 1
= 16 + 0 + 0 + 2 + 1
= 19
and, 101012 = 1 x 24 + 0 x 23 + 1 x 22 + 0 x 21 + 1 x 20
= 1 x 16 + 0 x 8 + 1 x 4 + 0 x 2 + 1 x 1
= 16 + 0 + 4 + 0 + 1
= 21
so, sum of both digit will be = 19 + 21 = 40
now, in binary form it can be represented as = 101000
b) Write the number 0.0101 as a power of 10.
Solution: The number 0.101 can be represented in the power of 10 as
1.01 x 10-1
Question 6:
As a promotional offer, a new hair salon offered its services at 20% discount for the first 2
weeks. Janice and her friends took advantage of the bargain and had their hair done for a total
amount of £100. Show your working.
Working notes :
Given, price paid for hair cut is £100 (selling price)
and, Discount offered at 20%
so, actual price will be = (100 / 100 - D%) x SP
3

= (100 / 80) x 100
= £125
a) What were the total savings made?
Solution: The total savings were:
Actual Price – Selling Price
= 125 – 100
= £25 (Answer).
b) Work out the average savings amount if 4 hairdos were done?
Solution: If 4 hairdos were done, then average savings will be –
25 / 4 = £6.25 (Answer)
Question 7:
Here are seven numbers - 5 12 12 8 4 10 5
a) Work out the mean of the seven numbers.
Solution : Mean of numbers are calculated by –
M = sum of numbers = 5 + 12 + 12 + 8 + 4 + 10 + 5 = 56 = 8
Total numbers 7 7
b) What is the mode of the seven numbers?
Solution : Mode is considered as the number which is repeated maximum time. In given data,
the most repeat is 12 (two times).
Question 8:
80 men and 120 women were asked if they enjoyed watching football.
Altogether 3 / 5 of the people said yes.
9 / 10 of the men said yes.
What fraction of the women said yes?
Solution: Number of Men = 80
Number of Women = 120
So, Total Men and Women = 80 + 120 = 200
Number of people who said yes out of 120 can be calculated by-
3/5 of 200 = 3/5 x 200 = 120
Number of men who said Yes = 9/10 of Men
4

= 9/10
= 72
So, Number of Women who said yes out of 120 are
120 – 72 = 48
Then, in the form of fraction, Women who said Yes would be calculated as
48/120 = 2/5
Question 9:
The table shows information about the marks of 20 students in a test.
Marks Frequency fx
14 2 28
15 5 75
16 4 64
17 4 68
18 5 85
Total 20 320
Students who scored less than the mean mark have to retake the test. How many students have to
retake the test?
Solution : Mean when frequency is given, can be calculated as –
‾x = ∑f x / ∑f
= 320 / 20
= 16 (Answers)
Question 10
Which fraction is bigger - 3/5 or 5/9?
Solution: Take LCM of denominators of both fractions as – 5 and 9
it will be – 45
So, 3/5 = 3 x 9 / 5 x 9 = 27/45
While, 5/9 = 5 x 5 / 9 x 5 = 25/45
5

So, 3/5 > 5/9 (Answer).
Section 2
11.
(a.)
GGG Consulting
Weekly Payroll
First
Name Surname
Gend
er
Hourly
Rate
Hrs
Worked
Gross
Amount Deductions
Net
Amount
Andy Brayton M £15.00 30 £450.00 £67.50 £382.50
Brendan Philiphs M £24.00 32 £768.00 £115.20 £652.80
Bronwyn Dykes F £22.00 20 £440.00 £66.00 £374.00
Candice Marfouche F £18.00 25 £450.00 £67.50 £382.50
Charlotte Messi F £17.00 30 £510.00 £76.50 £433.50
Denise Bolten F £21.00 35 £735.00 £110.25 £624.75
Everett Castlemain M £25.00 30 £750.00 £112.50 £637.50
Fred Patridge M £18.00 40 £720.00 £108.00 £612.00
Harry Charleston M £30.00 30 £900.00 £135.00 £765.00
Julia Morkoe F £25.00 28 £700.00 £105.00 £595.00
Patrice Neville F £20.00 35 £700.00 £105.00 £595.00
Richard Clement M £30.00 30 £900.00 £135.00 £765.00
Sandra Smith F £14.00 26 £364.00 £54.60 £309.40
Sunil Praveen M £23.00 28 £644.00 £96.60 £547.40
Tanika Hall F £12.00 28 £336.00 £50.40 £285.60
6

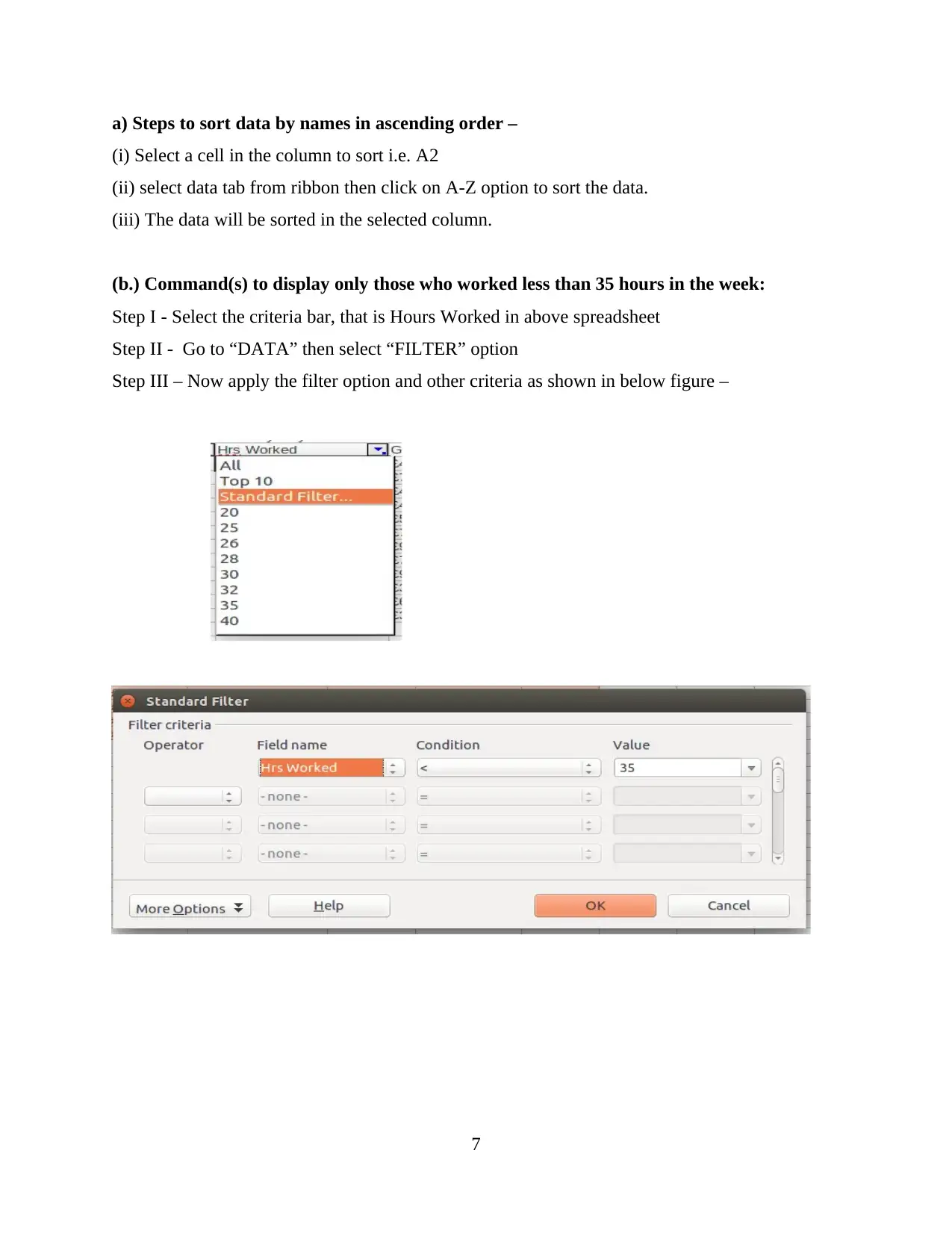
a) Steps to sort data by names in ascending order –
(i) Select a cell in the column to sort i.e. A2
(ii) select data tab from ribbon then click on A-Z option to sort the data.
(iii) The data will be sorted in the selected column.
(b.) Command(s) to display only those who worked less than 35 hours in the week:
Step I - Select the criteria bar, that is Hours Worked in above spreadsheet
Step II - Go to “DATA” then select “FILTER” option
Step III – Now apply the filter option and other criteria as shown in below figure –
7

c) How many people earn above average amount?
Solution : Step 1: Find average of column H first as shown below :-
Net
Amount
382.5
652.8
374
382.5
433.5
624.75
637.5
612
765
595
595
765
309.4
547.4
285.6
530.79
67
As per this table shown above, the average amount is £530.79
Therefore, using CountIf Command as (=COUNTIF(H5:H19,">530") then number of people
who earned more than average amount are 9.
8

d) state a type of graph or chart that will be suitable for representing the Net Amount information
To represent the net amount information, bar chart is made as shown below
e) In which column(s) might replication have been used?
Replication in spreadsheet is used to identity columns as per subscription types, that
allows to manage the columns in manual way or have replication manage them automatically. In
above data, in first column, replication can be used.
f) What formula results in the value in cell H20?
To find the grand total, SUM Command can be used as – (=Sum(H5:H19)
It will give – £7961.95.
9

ASSESSMENT 2
(a.) Totals, mean, median and standard deviation:
Name Campus Marital Food Clothings Entertainment Charitable
Giving
Jenny London S 160 230 80 0
Annie Manchester S 180 220 50 10
Haddy Manchester M 255 145 45 15
Martin Birmingham S 240 165 100 0
Ahmed London M 375 195 140 10
Sean London S 185 135 130 20
Alice London M 260 260 70 20
Belinda London M 320 140 105 15
Benjie Birmingham S 245 230 60 40
Barbara Manchester M 305 150 100 0
Liam Birmingham M 400 80 100 20
Totals: 2925 1950 980 150
Mean 265.90
91
177.272
7 89.09091
13.6363
6
Median 255 165 100 15
Standard deviation 77.936
45
53.9612
7 31.04981
11.8513
5
Working notes:
For food:
Food(x) (X- Mean) (X-Mean)2
160 -105.91 11216
.73554
180 -85.90909091 7380.
371901
255 -10.90909091 119.0
082645
10