Maths for Construction - Numerical Methods Assignment

This document presents a comprehensive solution to a maths assignment centered around construction applications. The assignment covers a range of mathematical concepts, including solving quadratic equations, analyzing lift and velocity relationships, working with arithmetic and geometric sequences, and applying logarithmic and exponential functions. It delves into statistical analysis, such as calculating mean, variance, and standard deviation from customer data, and using Kolmogorov-Smirnov and Shapiro-Wilk tests. The solution also addresses vector analysis, including calculating angles between vectors and determining vector equations. Furthermore, it explores bending moment functions, temperature modeling with exponential decay, and applying logarithmic and exponential equations to various scenarios. The document provides a detailed breakdown of each problem, offering step-by-step solutions and interpretations, making it a valuable resource for students studying mathematics in a construction context.

MATHS FOR CONSTRUCTION
Name of Student
Institution Affiliation

Task 1
Scenario 1
A=LW; L=w+3.2
26.5= (w+3.2) w; w2+3.2w-26.5=0
w=−3.2 ± √3.22−(4 × 1×−26.5)
2
=4.4 or -10.8
(b)
Lift =k × ρ ×V 2 × A
L = (1/2) d v2 s CL
The angle of attack and CL are related and can be found using a Velocity Relationship Curve
Graph
Scenario 2
a)
65 miles → 60 seconds
65 miles= (65 ×1760 /0.91) m=104104 m
Speed in m/s=104104/60=1735 m/s
65 miles=1 hour; 100 miles=10/65=1.54 hours

30 miles/gallon
1 gallon→3.78 liters
1 mile →1.61 km
30 miles →(30*1.61) km
Consumption in litters/km
=3.78/ (30*1.61)=0.078liters/km
Fuel consumption for the whole journey
{ 3.78
30 ×1.61 × 100
1.61 }=4.844
b)
L = (1/2) d v2 s CL
L = Lift, which must equal the airplane's weight in pounds
d = density of the air. This will change due to altitude. These values can be found in
a I.C.A.O. Standard Atmosphere Table.
v = velocity of an aircraft expressed in feet per second
s = the wing area of an aircraft in square feet
CL = Coefficient of lift, which is determined by the type of airfoil and angle of attack.
Scenario 3
1)
6th term

nth term=a+ ( n−1 ) d
d=2/3b-b=-1/3b
6th term=b+ (6-1)*-1/3b
=-2/3b
kth term
kth term=a+ (k-1)*-1/3b
20th term=15; 20th term=b-19/3b=-16/3b
−16
3 b=15 ; b=−45
16
Sum of the first 20 terms
Sn= n
2 ( a+ an ) = 20
2 (−45
16 +15)
=121.875
nth term=arn−1
2)
20th term=1 × 1
2
19
= 1
2
19
Sum to infinity
Sn= a .1(1−rn )
1−r

lim
n → ∞
a(1−rn)
1−r
Since |r|<1, then rn
→ 0 as n → ∞
Hence
S∞ = a
1−r = 1
1−1
2
=2
2Log (3x) + Log (18x) = 27
log (3x) 2+log 18x=27
9x2+18x=27
X2+2x-3=0
x=−2 ± √22− ( 4 ×1 ×−3 )
2 =1∨−3
3)
2 LOGe (3x) + LOGe (18x) = 9
LOGe (3x) 2+LOGe (18x) = 9
3x2+18x=9
9x2+18x-9=0
X2+2x-1=0

¿−2± √ 22 − ( 4 × 1×−1 )
2 =0.414∨−2.414
Cosh(X) + Sinh(X) = 5
ex+e−x
2 +( ex−e−x
2 )=9
ex+e−x−ex+ e−x
2 =9; 2 ex
2 =9
ex=9
Let ex be p
p=9
x=ln 9=2.19
Cosh (2Y) - Sinh (2Y) = 3
Cosh (2Y) = 1
2 ( e2 y+ e−2 y ) ; Sinh (2Y) = 1
2 ( e2 y−e−2 y )
( e2 y +e−2 y )− ( e2 y−e−2 y ) =3
( e2 y +e−2 y )− ( e2 y +e−2 y )=3
2 e−2 y−3=0 ; e−2 y= 2
3
2 y=ln 2
3 → y= 1
2 ln 2
3

Cosh (K) * Sinh (K) = 2
Cosh (K) = 1
2 ( e2 y+ e−2 y ) ; Sinh (K) = 1
2 ( e2 y−e−2 y )
( e2 y +e−2 y )− ( e2 y−e−2 y ) =2
( e2 y +e−2 y )− ( e2 y +e−2 y )=2
2 e−2 y−3=0 ; e−2 y= 2
3
2 y=ln 2
3 → y= 1
2 ln 2
3
Cosh (M) / Sinh (M) = 2
Cosh (M) = 1
2 ( e2 y+ e−2 y ) ; Sinh (M) = 1
2 ( e2 y−e−2 y )
( e2 y +e−2 y )− ( e2 y−e−2 y ) =2
( e2 y +e−2 y )− ( e2 y +e−2 y )=2
2 e−2 y−3=0 ; e−2 y= 2
3
2 y=ln 2
3 → y= 1
2 ln 2
3
Task 2
Scenario 1

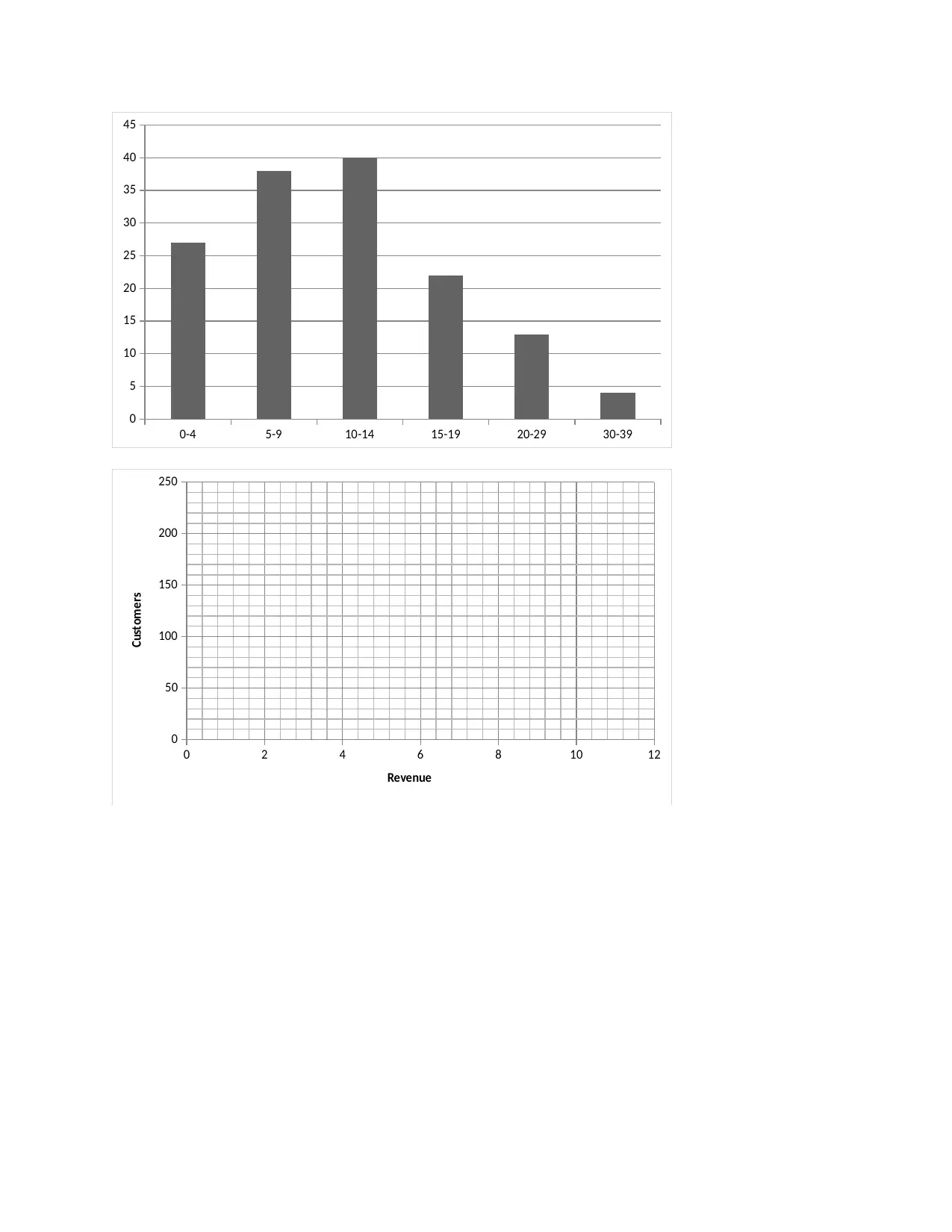
0-4 5-9 10-14 15-19 20-29 30-39
0
5
10
15
20
25
30
35
40
45
0 2 4 6 8 10 12
0
50
100
150
200
250
Revenue
Customers

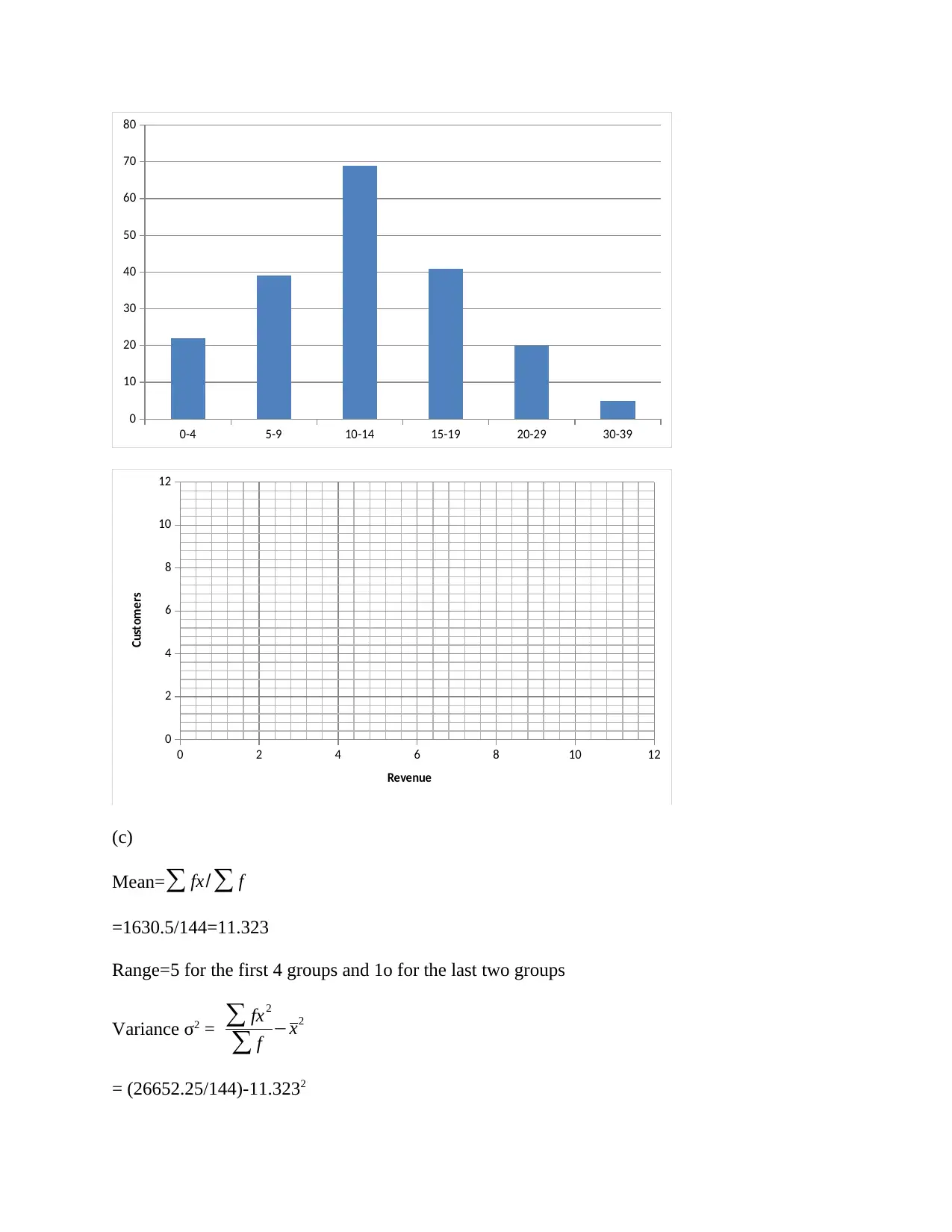
0-4 5-9 10-14 15-19 20-29 30-39
0
10
20
30
40
50
60
70
80
0 2 4 6 8 10 12
0
2
4
6
8
10
12
Revenue
Customers
(c)
Mean=∑ fx/ ∑ f
=1630.5/144=11.323
Range=5 for the first 4 groups and 1o for the last two groups
Variance σ2 = ∑ fx2
∑ f −x2
= (26652.25/144)-11.3232

56.875
Standard deviation=7.54
Scenario 2
Kolmogorov-Smirnov (K-S) and the Shapiro-Wilk (S-W) tests can be used in the testing of the
assumption that the data sample are extracted from a normally distributed population.
The probabilities given in the problem are cumulative i.e. till week 1, till week 2 etc. Individual
probabilities would be 0.10 in 1st week, 0.15 (0.25-0.10) in 2nd week, and so on.
Individual Failures/week = Total Quantity / Mean Life = 1000 / 3.45 = 289.9
Individual Replacement Cost = (Individual Failures per week) x (Individual replacement cost)
= 289.9 x 3 = Rs. 869.6
In the first week: 10 % (0.10) of the bulbs will fail out of 1000 bulbs i.e. 100
In the second week: 15 % of the bulbs will fail out of 1000 bulbs i.e. 150. Also, 10% of 100
replaced in the first week i.e. 10. TOTAL bulbs failed until second week = 160 (150+10)
Thus, replacing all the bulbs simultaneously at fixed interval & also to replace the individual
bulbs that fail in between will be economical or optimal after 4 weeks (optimal interval between
group replacements).
Interpretation:
1. The cost of only individual replacements id Rs. 869.6
2. The cost of combine policy i.e. group and individual replacement id Rs. 863.6
3. Hence the Policy-II is the optimum replacement policy
Hence, the bulbs shall be replaced every four weeks individually as well as in groups which
combine would cost Rs. 863.6 per week

[Note: "Yes we can, if..." A way to help solve this type of problem is to answer "Yes we can,
if..." In this case the question is, "Can it be concluded that the mean age of the population is not
30?" Answer, "Yes we can, if we can reject the null hypothesis that it is 30." Responding to
problems the same way all the time will lead to less confusion and less errors. ]
(1) Data
n = 10 = 20
= 27 = .05
(2) Assumptions
 simple random sample
 normally distributed population
(3) Hypotheses
: = 30
: 30
(4) Test statistic
as the population variance is known, we use z as the test statistic.
(a) Distribution of test statistic
if the assumption is correct and is true, the test statistic follows the standard normal distribution.
Therefore, we calculate a z score and use it to test the hypothesis.
(b) Decision rule
Reject if the z value falls in the rejection region. Fail to reject if it falls in the non-
rejection region.

Because of the structure of it is a two tail test. Therefore, reject if z -1.96 or z 1.96.
(5) Calculation of test statistic
(6) Statistical decision
the null hypothesis is rejected because z = -2.12 which is in the rejection region. The value is
significant at the .05 level.
(7) Conclusion
it is concluded that is not 30.
p = .0340
A z value of -2.12 corresponds to an area of .0170. Since there are two parts to the rejection
region in a two tail test, the p value is twice this which is .0340.
A problem like this can also be solved using a confidence interval. A confidence interval will
show that the calculated value of z does not fall within the boundaries of the interval. It will not,
however, give a probability.