Applied Numerical Methods Project 1 & 2: Triple Pendulum and Beams
VerifiedAdded on 2023/04/20
|15
|1932
|266
Project
AI Summary
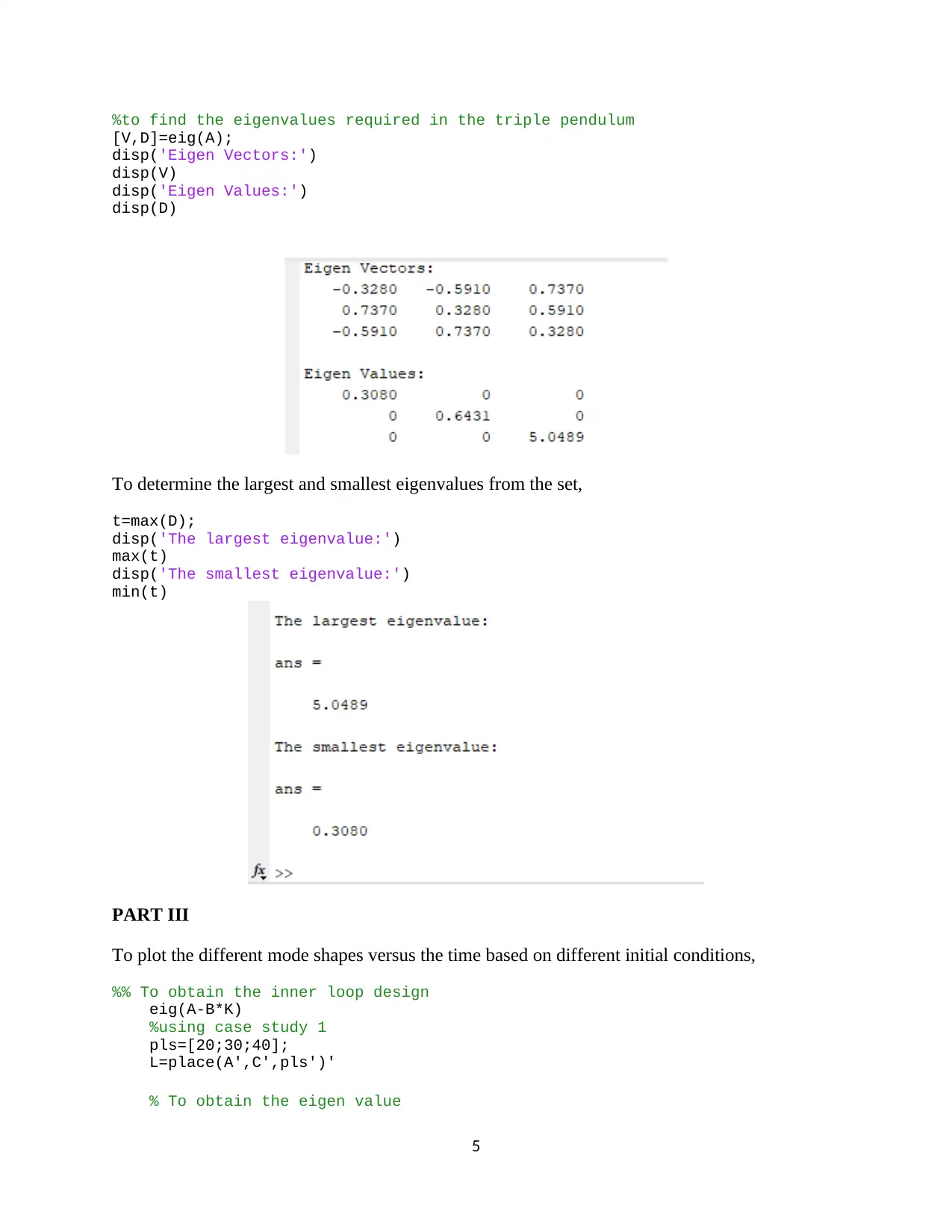
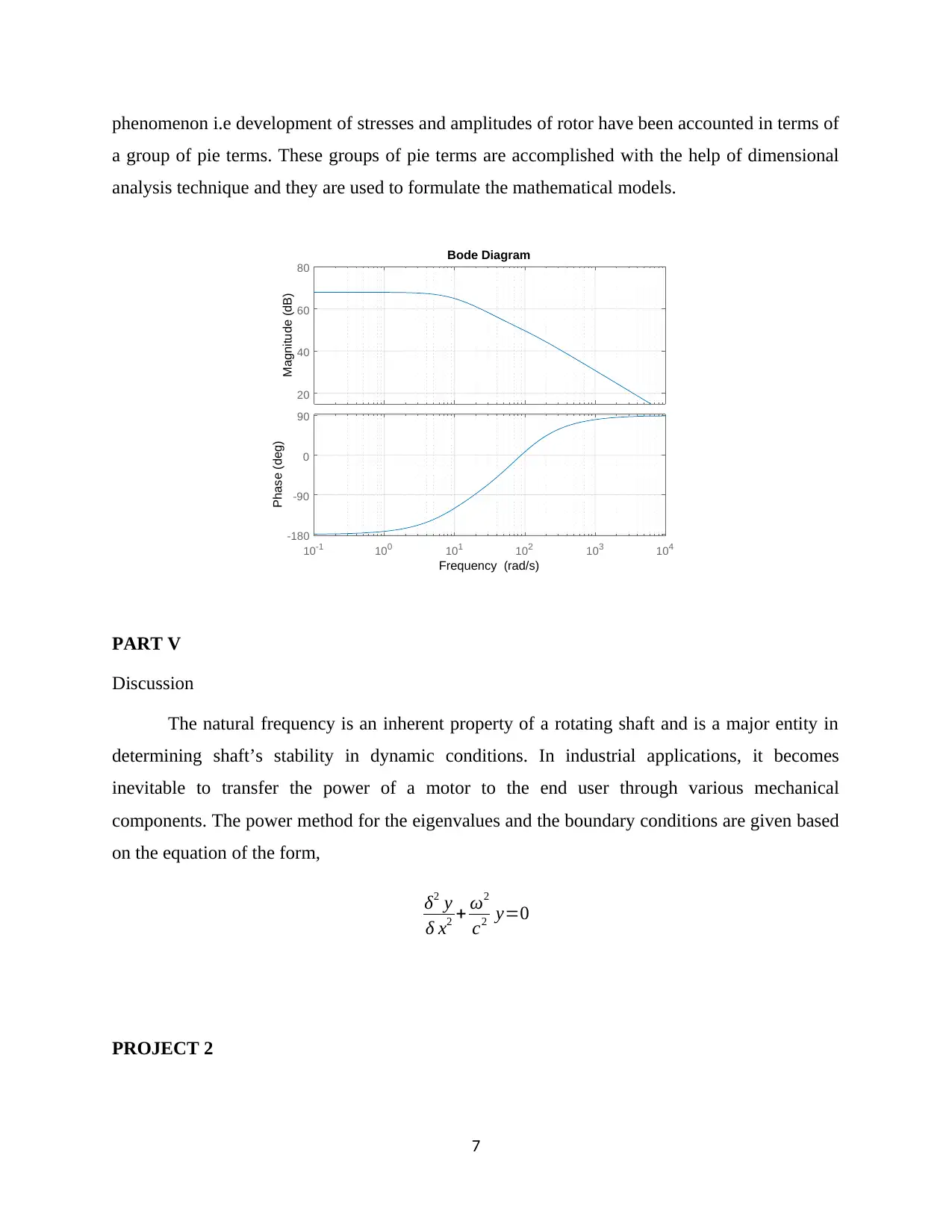
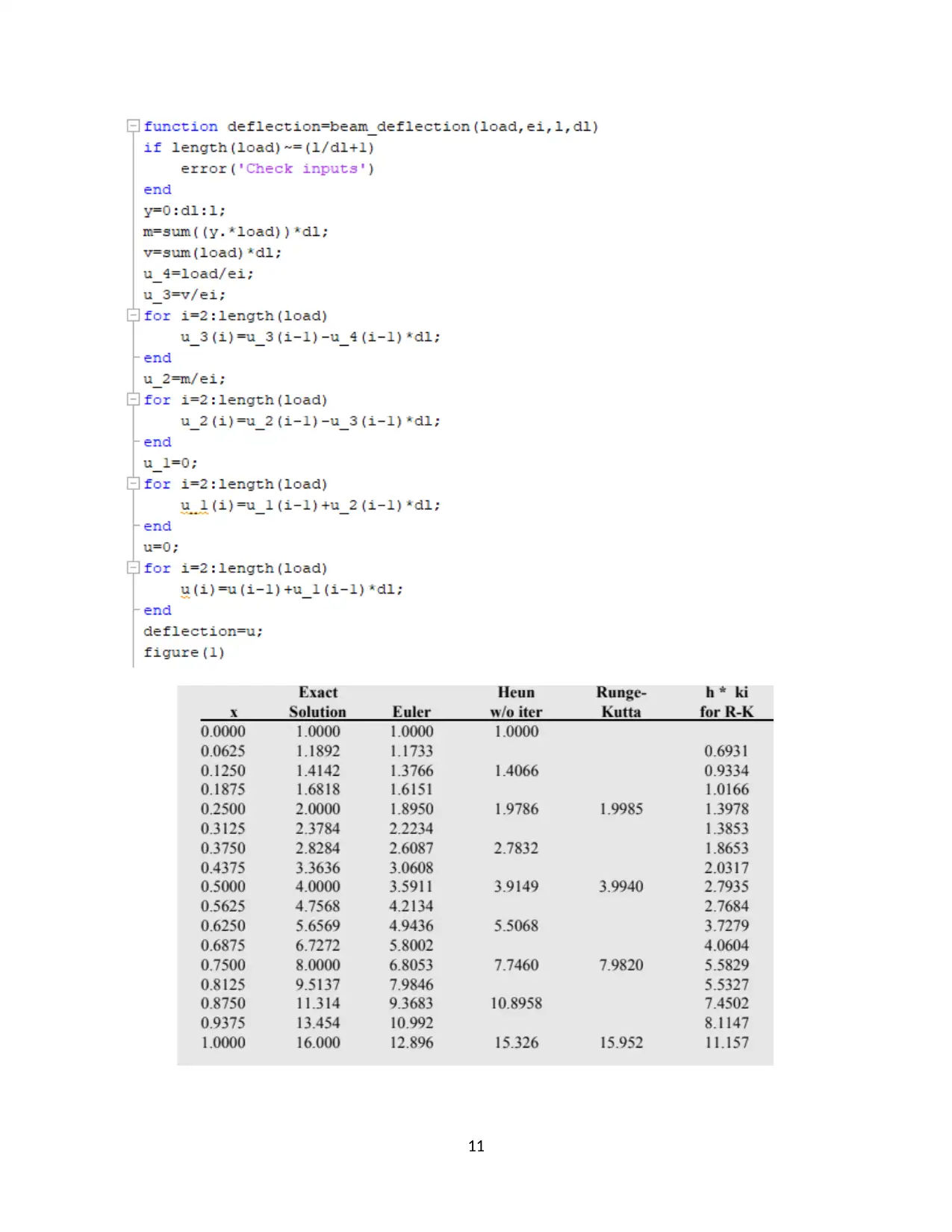
This project presents a comprehensive analysis of two mechanical engineering problems using applied numerical methods. Part I focuses on determining the natural frequencies of a triple pendulum's free vibration by formulating the equation of motion, deriving the eigenvalue problem, and obtaining analytical solutions. Part II involves implementing the problem in MATLAB to find eigenvalues and eigenvectors. Part III extends the MATLAB implementation to plot mode shapes versus time under various initial conditions, including system stability analysis, frequency response plots, and the design of an inner loop using control theory techniques such as the 'place' function and Bode diagrams. Part IV addresses the estimation of stresses in the shaft and rotor amplitudes. Part V provides a discussion on the natural frequency of a rotating shaft, including the power method for eigenvalues and boundary conditions. Project 2 focuses on the deflection analysis of an I-beam cantilever with a distributed load, utilizing analytical solutions for deflection and shear force calculations, and considering bending moments. Part II estimates deflection behavior using Runge-Kutta methods, and Part III provides a comparative discussion on the strength and deflection characteristics of T-beams, I-beams, and Z-beams, including strain diagram analysis and concluding that the I-beam is preferred for handling compressive and tensile pressures.
1 out of 15
















![[object Object]](/_next/static/media/star-bottom.7253800d.svg)