University Further Mathematics Assignment: Numerical Methods Solutions

This document presents a comprehensive solution to a Further Mathematics assignment, addressing various topics within numerical methods and calculus. The assignment covers solving equations graphically, analyzing the motion of objects using integration, and applying differential equations to model physical systems. It includes detailed solutions for definite integrals using the trapezoidal and Simpson's rules. Additionally, the assignment explores solving differential equations using Laplace transforms and iterative techniques like the Regula Falsi and Newton's methods to find the roots of equations. The solutions are presented step-by-step, demonstrating the application of mathematical concepts to solve complex problems. This resource is available on Desklib, a platform providing students with AI-based study tools.

Further Mathematics

Table of Contents
Question 1........................................................................................................................................1
Question 2........................................................................................................................................2
Question 3........................................................................................................................................2
Question 4........................................................................................................................................4
Question 5........................................................................................................................................5
Question 6........................................................................................................................................6
Question 7........................................................................................................................................6
Question 8........................................................................................................................................6
Question 9........................................................................................................................................6

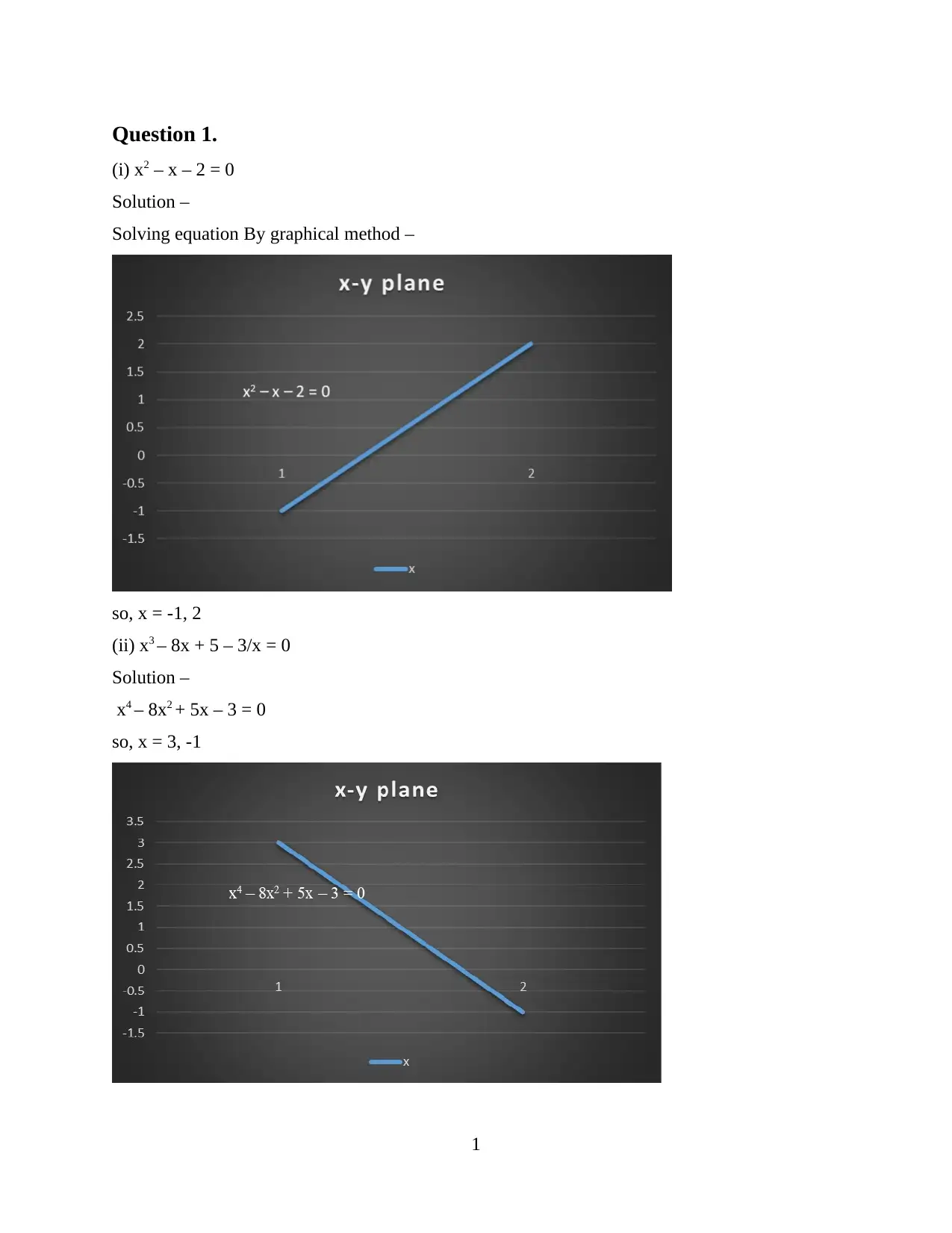
Question 1.
(i) x2 – x – 2 = 0
Solution –
Solving equation By graphical method –
so, x = -1, 2
(ii) x3 – 8x + 5 – 3/x = 0
Solution –
x4 – 8x2 + 5x – 3 = 0
so, x = 3, -1
1

Question 2
Given,
initial velocity (u) = 15m/s
Motion of object –
ds = u – gt
dt
where, g = 9.8 m/sec2
Height of object after 2 sec, if s = 0 when = 0
Integrate the given equation as –
∫ds = ∫(u – gt). dt
s = ut – gt2
putting all the values,
s = 15 x 2 – 9.8 x (2)2
= 30 – 39.2
= 9.2m
Question 3
Given
Movement of body in straight line given as –
d2s + a2s = 0
dt2
where, a is constant and s = c and ds/dt = 0 at t = 2π/a
Integrate the given equation as –
d2s = - a2s
dt2
∫d2s = ∫a2s
dt2
ds = a2s t + C
dt
taking, a as constant and s = c and ds/dt = 0 at t = 2π/a
a2 c (2π/a) + C = 0
ac. 2π + C= 0
C = 2πac
then,
2

ds = a2s t + 2πac
dt
3

Question 4
Using trapezoidal rule and Simpson’s rule
i) ∫30 √ (1 + x4). dx
Solution:
Δx = b – a
n
here, a = 0, b = 3, n = 8
= 3 – 0 = 3
8 8
so, intervals – x = {0, 3/8, 3/4, 9/8, 3/2, 15/8, 9/4, 21/8, 3}
so, f(x0) = √ (1 + (0)4) = 1
f(x1) = √ (1 + (3/8)4) = 1.009
f(x2) = √ (1 + (3/4)4) = 1.147
f(x3) = √ (1 + (9/8)4) = 1.613
f(x4) = √ (1 + (3/2)4) = 2.462
f(x5) = √ (1 + (15/8)4) = 3.655
f(x6) = √ (1 + (9/4)4) = 5.160
f(x7) = √ (1 + (21/8)4) = 6.962
f(x8) = √ (1 + (3)4) = 9.055
Trapezoidal rule
≈ Δx/2 [f(x0) + 2. f(x1) + 2. f(x2) + 2. f(x3) + 2. f(x4) + 2. f(x5) + 2. f(x6) + 2. f(x7) + f(x8)]
≈ 3/16 [1 + 2x1.009 + 2x1.147+ 2x1.613+ 2x2.462 + 2x3.655 + 2x5.160 + 2x6.962 + 9.055]
≈ 8.084
Simpson’s rule
≈ Δx/3 [f(x0) + 4. f(x1) + 2. f(x2) + 4. f(x3) + 2. f(x4) + 4. f(x5) + 2. f(x6) + 4. f(x7) + f(x8)]
≈ 1/8 [1 + 4x1.009 + 2x1.147 + 4x1.613 + 2x2.462 + 4x3.655 + 2x5.160 + 4x6.962 + 9.005]
≈ 10.462
ii) ∫31 2ln3x dx
Solution:
4

Δx = b – a
n
here, a = 0, b = 3, n = 8
= 3 – 1 = 1
8 4
so, intervals – x = {1, 5/4 3/2, 7/4, 2, 9/4, 5/2, 11/4, 3}
so, f(x0) = 2ln3(1) = 2.197
f(x1) = 2ln3(5/4) = 2.643
f(x2) = 2ln3(3/2) = 3.008
f(x3) = 2ln3(7/4) = 3.316
f(x4) = 2ln3(2) = 3.583
f(x5) = 2ln3(9/4) = 3.819
f(x6) = 2ln3(5/2) = -1.248
f(x7) = 2ln3(11/4) = 4.220
f(x8) = 2ln3(3) = 4.394
Trapezoidal rule
≈ Δx/2 [f(x0) + 2. f(x1) + 2. f(x2) + 2. f(x3) + 2. f(x4) + 2. f(x5) + 2. f(x6) + 2. f(x7) + f(x8)]
≈ 1/8 [2.197 + 2x2.643 + 2x3.008 + 2x3.316+ 2x3.583+ 2x3.819 + 2x(-1.248) + 2x4.220 +
4.394]
≈ 5.659
Simpson’s rule
≈ Δx/3 [f(x0) + 4. f(x1) + 2. f(x2) + 4. f(x3) + 2. f(x4) + 4. f(x5) + 2. f(x6) + 4. f(x7) + f(x8)]
≈ 1/12 [2.197 + 4x2.643 + 2x3.008 + 4x3.316+ 2x3.583+ 4x3.819 + 2x(-1.248) + 4x4.220 +
4.394]
≈ 6.102
5

Question 5
Given equation –
CR dV + V = E
dt
(a) Solve equation for V at t = 0 and V = 0
Solution –
CR dV + V = E
dt
dV = 1 . dt
(E – V) CR
ln(E – V) = -t/CR + k
E – V = ke(-t/CR)
V = E - ke(-t/CR)
at initial condition, at V = 0 and t = 0
k = E
therefore,
V = E (1 – e(-t/CR))
(b) Calculate V when E = 25V, C = 20 x 10-6 F, R = 200 x 103Ω and t = 3.0s
Using, above equation –
V = E (1 – e(-t/CR))
= 25 (1 – e^(-3/20 x 10-6 . 200 x 103))
≈ 13.192
6

Question 6
Oscillations of a damped mechanical system –
2 d2y + 6dy + 4.5 y = 0
dt2 dt
displacement expression using Laplace Transforms –
at t = 0, y = 0 and dy/dt = 4
Solution –
2 d2y + 6dy + 4.5 y = 0
dt2 dt
Divide the given equation by 2,
d2y + 3dy + 2.25 y = 0
dt2 dt
Now, take the Laplace transform on both side –
Ĺ d2y + 3 Ĺdy + 2.25 Ĺy = Ĺ(0)
dt2 dt
solving it –
f(s) = 4 .
s + 6s +2.25
7

Question 7
Roots of equation using two different iterative techniques
x4 – 3x 3 + 7x = 12
Solution
Regula Falsi method
let y(x) = x4 – 3x 3 + 7x – 12
y(2) = -6
y(3) = 9
so, root of this equation lies between 2 and 3
Then, first approx.
x1= a f(b) – b f(a) /f(b) – f(a)
= 2 x (9) – 3 x (-6)/ 9 – (-6)
= 2.4
f(2.4) = (2.4)4 – 3 (2.4)3 + 7 (2.4) – 12
= 33.1776 – 41.472 + 16.8 – 12
= -3.5
so, root lies between 2.4 and 3
Then, second approx.
x2 = a f(b) – b f(a) /f(b) – f(a)
= 2.4 x (9) – 3 x (-3.5)/ 9 – (-3.5)
= 2.5
f(2.5) = (2.5)4 – 3 (2.5)3 + 7 (2.5) – 12
= 39.0625 – 46.875 + 17.5 – 12
= -2.3
so, root lies between 2.5 and 3
Then, third approx.
x3 = a f(b) – b f(a) /f(b) – f(a)
= 2.5 x (9) – 3 x (-2.3)/ 9 – (-2.3)
= 2.6
so, root of the given equation is 2.5
8

Newton’s iterative method –
let y(x) = x4 – 3x 3 + 7x – 12
y(2) = -6
y(3) = 9
so, root of this equation lies between 2 and 3
First approximation
x1 = (a+b)/2
= (2+3)/2 = 2.25
so, f(2.25) = (2.25)4 – 3 (2.25)3 + 7 (2.25) – 12
= 25.6289062 – 34.171875 + 15.75 – 12
= -4.8
Hence, root lies between 2.25 and 3
Second approximation
x2 = (2.25+3)/2
= 2.625
so, f(2.625) = (2.625)4 – 3 (2.625)3 + 7 (2.625) – 12
= -0.4
Hence, root lies between 2.625 and 3
Third approximation
x3 = (2.625+3)/2
= 2.8
so, f(2.8) = (2.8)4 – 3 (2.8)3 + 7 (2.8) – 12
= 3.2 which is positive
Hence, root of the equation is 2.8
9

Question 9
d2ϴ + 4 dϴ + 4ϴ = 8
dt2 dt
solve at t = 0, ϴ = dϴ/dt = 2
Solution –
Since the general solution of
(D2 + 4D + 4) ϴ = 8
substitute m for D
m2 + 4m + 4 = 8
m2 + 4m – 4 = 0
or, m = -2 ±2√ 2
As general solution of differential equation when roots are real
ϴ = (At + B)e^(-2 ±2√ 2)t
at t = 0 and ϴ = 0
2 = (A x 0 +B)e0
B = 2
while,
dϴ/dt = (At + B) (-2 ±2√ 2). e(-2 ±2√ 2)t + Ae(-2 ±2√ 2)t
2 = (0 + B) (-2 ±2√ 2). e0 + A. e0
A = 4√ 2
So, ϴ = (4√2t + 2)e^(-2 ±2√ 2)t
10