Numerical Techniques Assignment Solution - Coursework

This document presents a comprehensive solution to a numerical techniques assignment, addressing a range of mathematical problems. The assignment covers solving quadratic equations using the quadratic formula, systems of linear equations using the elimination method, and problems involving both algebraic and geometric concepts. It includes detailed solutions for finding the roots of quadratic equations, solving simultaneous equations, and analyzing graphical representations of functions. Furthermore, the assignment delves into probability calculations, including conditional probability and statistical measures like mean and median. Trigonometry is also applied to solve problems related to distance and angles. The solution provides step-by-step explanations and calculations, demonstrating the application of various mathematical principles to solve real-world scenarios. The document concludes with a list of references to support the solution.

NUMERICAL
TECHNIQUES

TABLE OF CONTENTS
QUESTIONS...................................................................................................................................3
REFERENCES................................................................................................................................9

QUESTIONS
2.
a. 3x2-4x-2 = 0
By using the formula,
x=−b ± √ b2−4 ac
2 a (Salas, El-Tantawy and Aljahdaly, 2021)
The degree of the equation is 2 which is the highest power of variable x.
This is why, there can be 2 solutions found or the 2 values of x can be found.
By putting the values of b = -4, a = 3 and c = -2
x = 4 +- √42 – 4*3*-2 / 2*3
= (4 + 2 √10) / 6 or (4 - 2 √10) / 6
b. 4x – 3y = 18 and 5x + 2y = 11
The elimination method can be used for solving this equation and to get the value of x.
There are two linear equations given which means the degree of both the equations is 1.
Elimination method deals in eliminating one of the variables and then finding the value of the
other one by equating the value of the first one in both the equations (Snyder Jr and et.al., 2017).
4x – 3y = 18 (Multiplying it with 2)
5x + 2y = 11 (Multiplying it with 3)
The equations obtained are:
8x – 6y = 36
15x +6y = 33
Eliminating y, we get 23x = 69
x = 3
Putting the value of x = 3 in equation 1,
4*3 – 3y = 18
3

12- 3y = 18
-3y = 6
y = -2
c. x2 + y2 = 5
x + y = 3
Since, x + y = 3.
(x + y)2 = 9
x2 + y2 + 2xy = 9
5 + 2xy = 9 (Since, x2 + y2 = 5)
2xy = 4
xy = 2
x + y = 3
x = 3-y
(3-y) y = 2
3y –y2 – 2 = 0
y2 -3y + 2 = 0
By applying the quadratic formula for solving the equations,
x=−b ± √ b2−4 ac
2 a
y = (3 +- √9-4*1*2)/ 2*1
= (3+-√1) / 2
= 3+1/2 or 3-1/2
= 2 or 1
Values of x can be found by making use of equation x + y = 3
Values can be found as 1 or 2 (Ren, Ma and Yu, 2019).
4

d. i. x+1
4 + x +2
3 =12−x
3 (x+1) + 4 (x+2) = 12 (12-x) (Wu, Sun and Chen, 2018)
3x + 3 + 4x + 8 = 144 – 12x
7x + 11 = 144 – 12x
7x + 12x = 144 – 11
19x = 133
x = 133/ 19
= 7
ii. 3 x +1
2 = 9 x−5
5
5 (3x + 1) = 2(9x - 5)
15x + 5 = 18x – 10
15x – 18x = -10 -5
-3x = -15
x = 5
3. y=5 x−x2
a.
x -1 0 1 2 3 4 5 6
y -6 0 4 6 6 4 0 -6
5

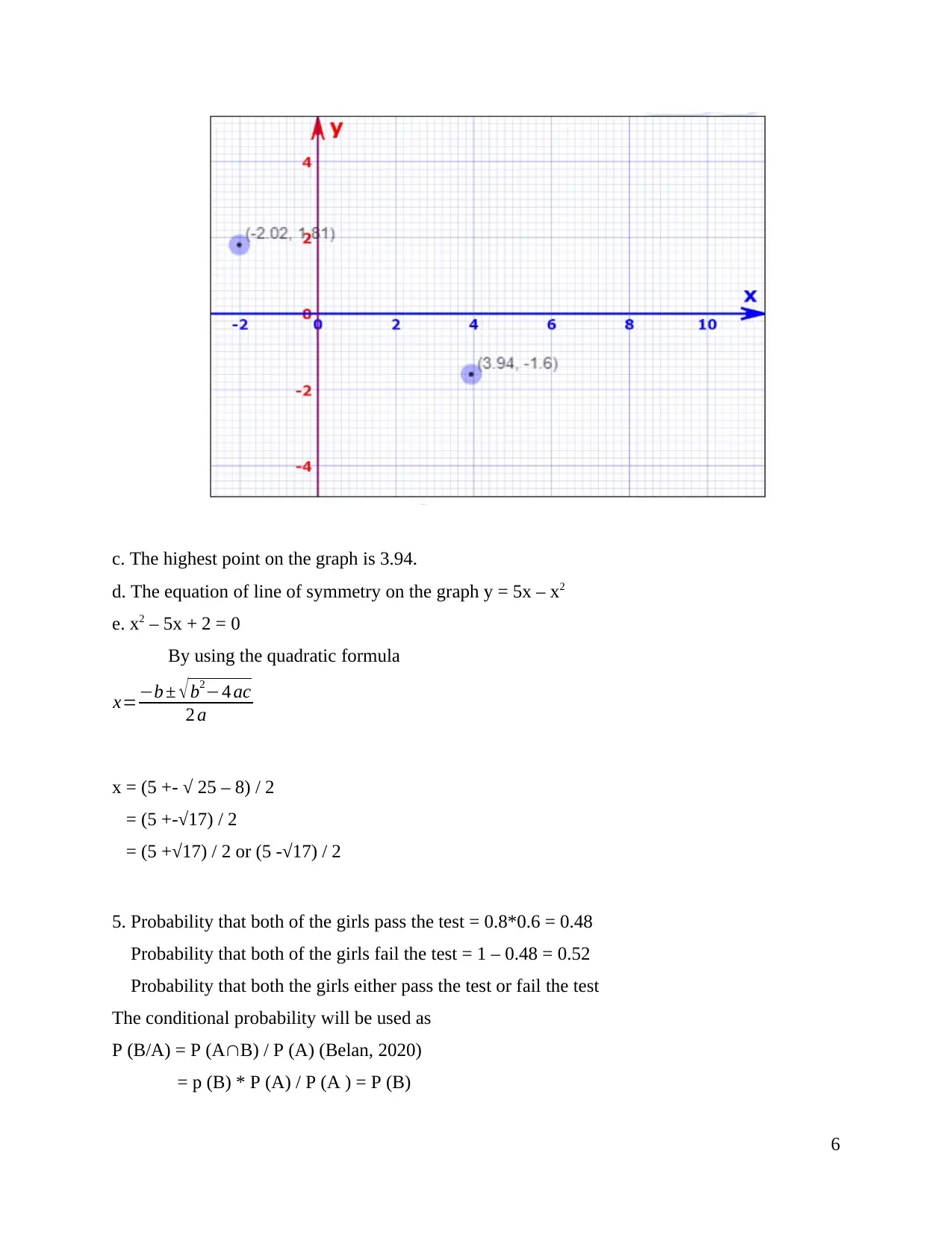
c. The highest point on the graph is 3.94.
d. The equation of line of symmetry on the graph y = 5x – x2
e. x2 – 5x + 2 = 0
By using the quadratic formula
x=−b ± √ b2−4 ac
2 a
x = (5 +- √ 25 – 8) / 2
= (5 +-√17) / 2
= (5 +√17) / 2 or (5 -√17) / 2
5. Probability that both of the girls pass the test = 0.8*0.6 = 0.48
Probability that both of the girls fail the test = 1 – 0.48 = 0.52
Probability that both the girls either pass the test or fail the test
The conditional probability will be used as
P (B/A) = P (AB) / P (A) (Belan, 2020)
= p (B) * P (A) / P (A ) = P (B)
6

= 0.52/ 0.8
= 0.65
b. Modal score is the score which is heaving highest frequency which means the modal score is 7
which is having highest frequency of 15 (Dewanto, Budiyono and Pratiwi, 2017).
Mean score = Sum of scores/ Number of scores
= 77/11
= 7
Median score can be found by formula n+1 / 2
11+1 / 2
=> 6th score.
Score = 7 and frequency = 15.
4. a. x distance = 50 sin 50
y distance = 40 sin 150 (Gaunt and Merkle, 2020)
Total distance magnitude = 50 sin 50 + 40 sin 150 + (50 cos 50 + 40 cos 150)i
= 50 * 0.76 + 40 * 0.5 + (50 * 0.64 + 40 * -0.86)i
= 38 + 20 + (32 – 34.4)i
= 58 + (-2.4)i
= 58 kms.
b. i. Triangle ABC can be drawn with base AC which is the distance of the worm from base of
tree.
Height of the tree is BC which is 12 m.
The hypotenuse of AB which is the distance travelled by the bird to the worm.
i. tan A = BC/ AC
tan 34 degree = 12/ AC
0.67 = 12/ AC
7

AC = 12/0.67
AC = 17.91 m
Therefore, the distance between the worm and the foot of the ground is 17.91 m (approx).
ii. Sin 34 degree = Perpendicular / Hypotenuse (Kim and et.al., 2019)
0.56 = 12/ AB
AB = 12/0.56
AB = 21.42 m.
Therefore, distance of the bird from the worm is 21.42 m.
8

REFERENCES
Books and Journals
Belan, S., 2020. Median and mode in first passage under restart. Physical Review Research. 2(1).
p.013243.
Dewanto, M.D., Budiyono, B. and Pratiwi, H., 2017, August. Students’ Error Analysis in
Solving The Math Word Problems of High Order Thinking Skills (HOTS) Type on
Trigonometry Application. In 1st Annual International Conference on Mathematics,
Science, and Education (ICoMSE 2017) (pp. 126-131). Atlantis Press.
Gaunt, R.E. and Merkle, M., 2020. On the mode and median of the generalized hyperbolic and
related distributions. arXiv preprint arXiv:2002.01884.
Kim, J. and et.al., 2019, June. Mixed reality for learning programming. In Proceedings of the
18th ACM International Conference on Interaction Design and Children (pp. 574-579).
Ren, B., Ma, W.X. and Yu, J., 2019. Rational solutions and their interaction solutions of the (2+
1)-dimensional modified dispersive water wave equation. Computers & Mathematics
with Applications. 77(8). pp.2086-2095.
Salas, A.H., El-Tantawy, S.A. and Aljahdaly, N.H., 2021. An exact solution to the quadratic
damping strong nonlinearity Duffing oscillator. Mathematical Problems in
Engineering, 2021.
Snyder Jr, J.W. and et.al., 2017. A direct-compatible formulation of the coupled perturbed
complete active space self-consistent field equations on graphical processing units. The
Journal of chemical physics. 146(17). p.174113.
Wu, G., Sun, J. and Chen, J., 2018. Optimal linear quadratic regulator of switched systems. IEEE
transactions on automatic control. 64(7). pp.2898-2904.
9