Optimizing Product Mix and Profitability at O'Neill Enterprises

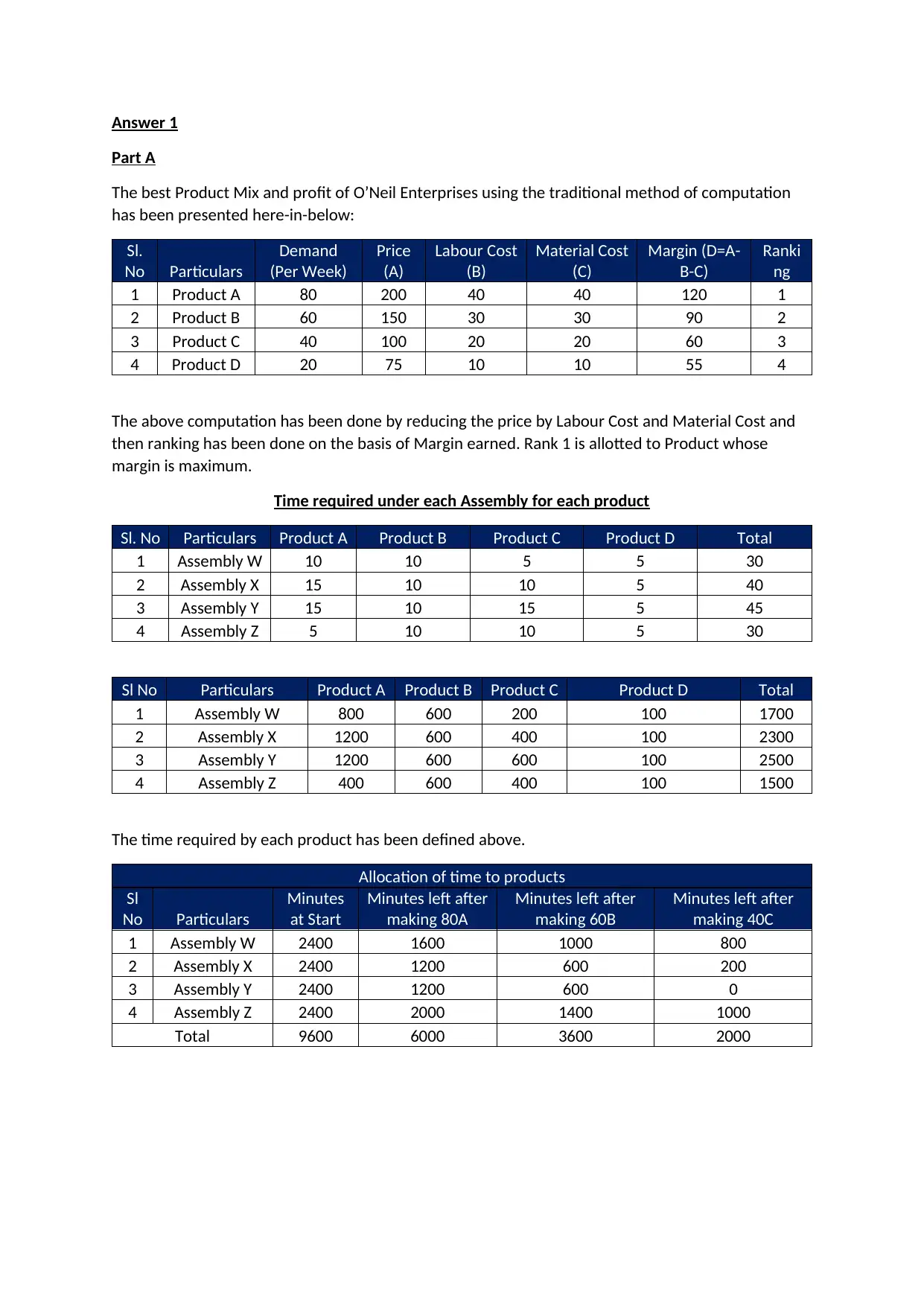
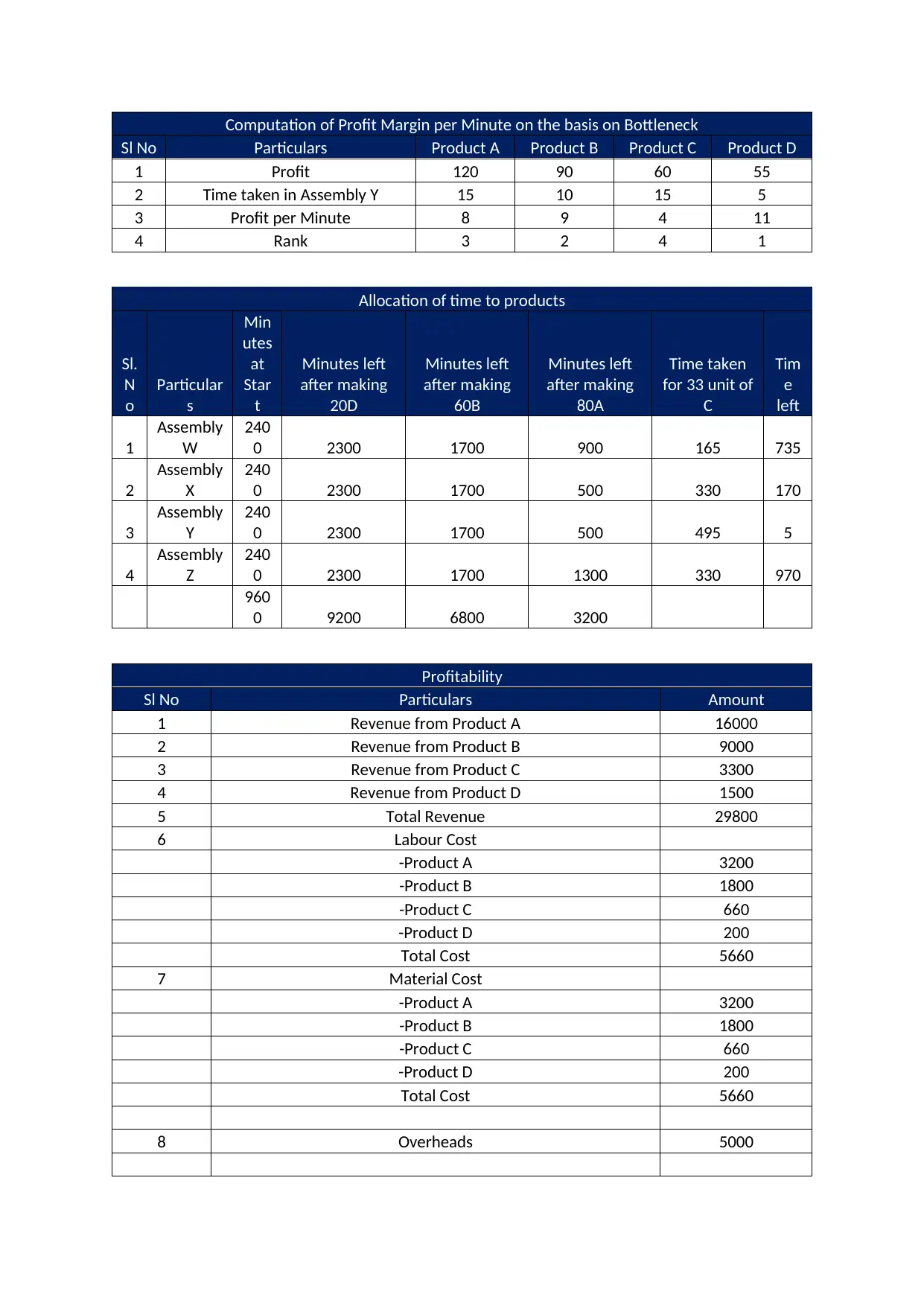
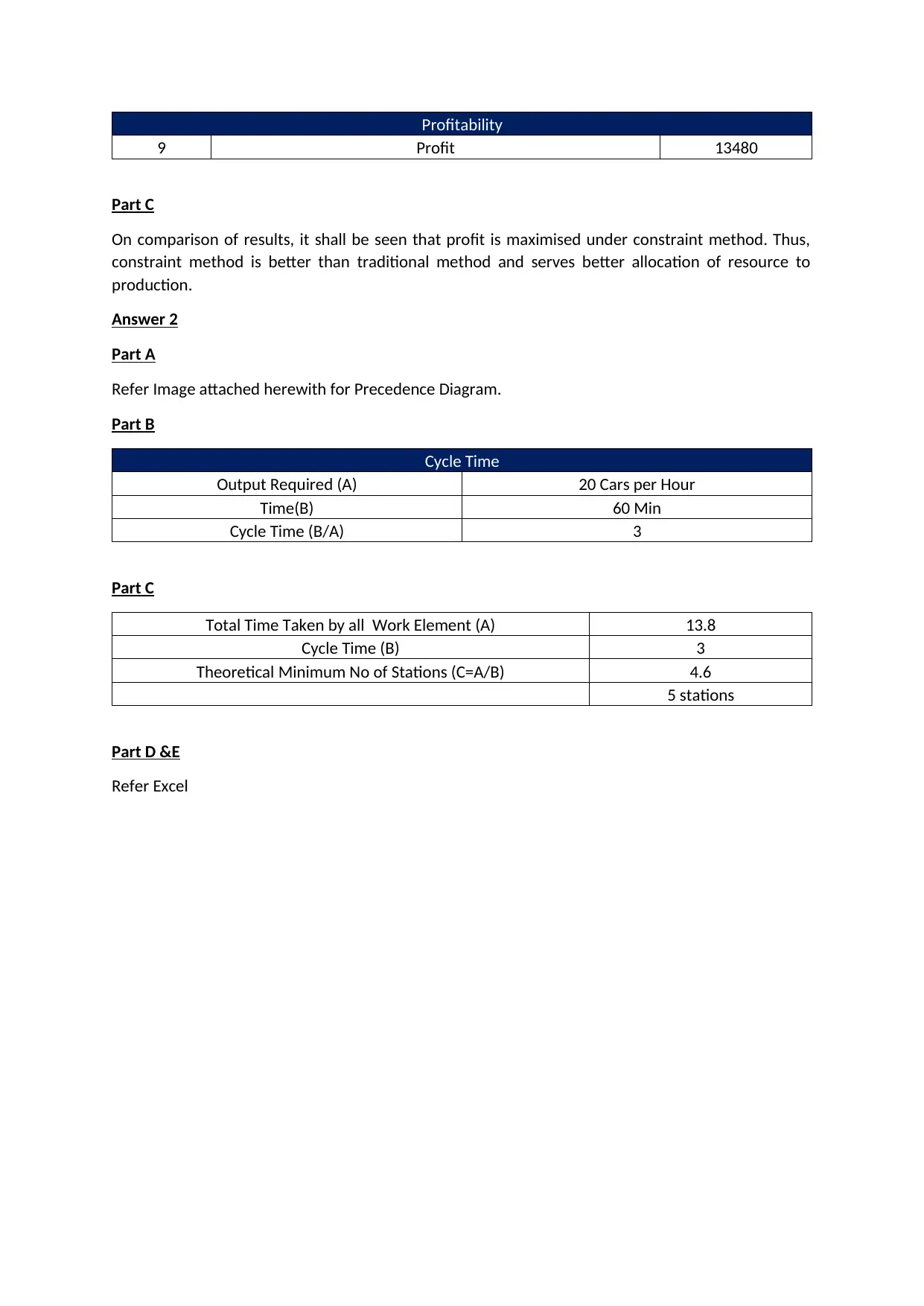
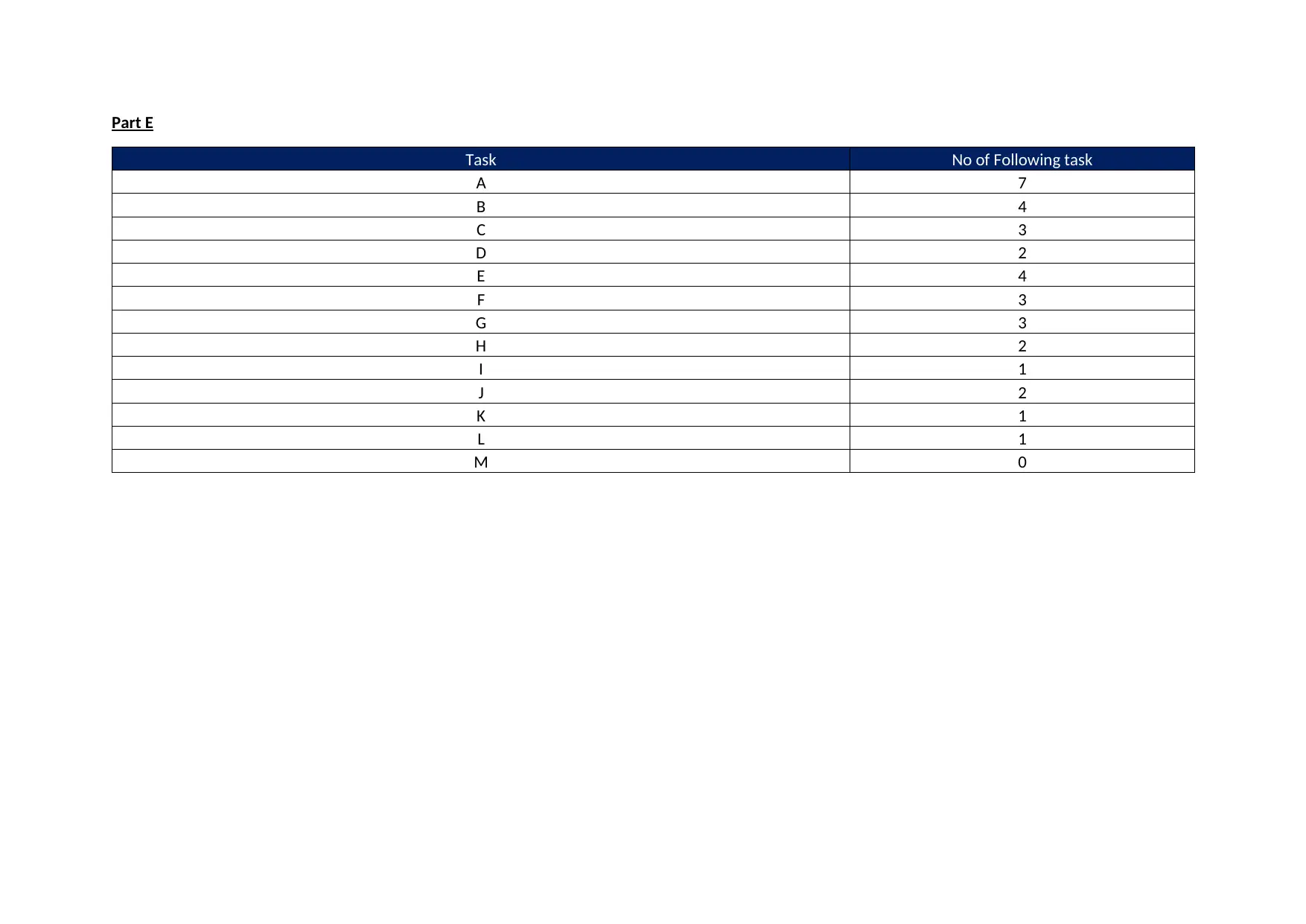
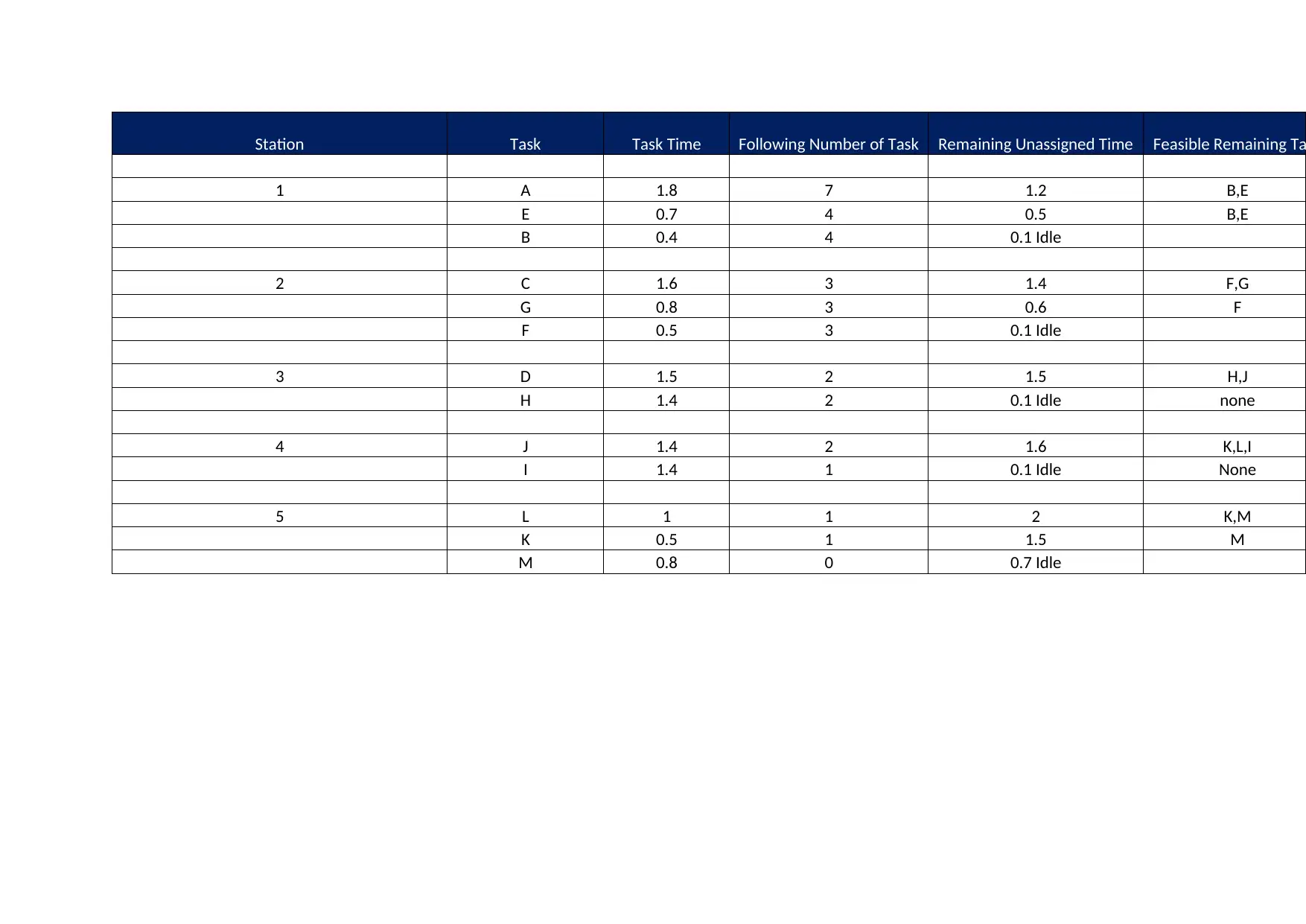
This assignment provides a detailed solution to a product mix optimization problem for O'Neill Enterprises. It begins by determining the best product mix and profit using the traditional method, ranking products based on margin. Then, it applies the constraint method, identifying bottleneck factors and calculating profit margin per minute to optimize resource allocation. The solution compares the results of both methods, concluding that the constraint method maximizes profit more effectively. Additionally, the assignment includes a precedence diagram, cycle time calculation, and theoretical minimum number of stations, along with task assignments and idle time analysis for a production line scenario. This comprehensive analysis demonstrates how to strategically allocate resources and optimize production processes for enhanced profitability. Desklib provides access to similar solved assignments and resources for students seeking assistance with their studies.

Answer 1
Part A
The best Product Mix and profit of O’Neil Enterprises using the traditional method of computation
has been presented here-in-below:
Sl.
No Particulars
Demand
(Per Week)
Price
(A)
Labour Cost
(B)
Material Cost
(C)
Margin (D=A-
B-C)
Ranki
ng
1 Product A 80 200 40 40 120 1
2 Product B 60 150 30 30 90 2
3 Product C 40 100 20 20 60 3
4 Product D 20 75 10 10 55 4
The above computation has been done by reducing the price by Labour Cost and Material Cost and
then ranking has been done on the basis of Margin earned. Rank 1 is allotted to Product whose
margin is maximum.
Time required under each Assembly for each product
Sl. No Particulars Product A Product B Product C Product D Total
1 Assembly W 10 10 5 5 30
2 Assembly X 15 10 10 5 40
3 Assembly Y 15 10 15 5 45
4 Assembly Z 5 10 10 5 30
Sl No Particulars Product A Product B Product C Product D Total
1 Assembly W 800 600 200 100 1700
2 Assembly X 1200 600 400 100 2300
3 Assembly Y 1200 600 600 100 2500
4 Assembly Z 400 600 400 100 1500
The time required by each product has been defined above.
Allocation of time to products
Sl
No Particulars
Minutes
at Start
Minutes left after
making 80A
Minutes left after
making 60B
Minutes left after
making 40C
1 Assembly W 2400 1600 1000 800
2 Assembly X 2400 1200 600 200
3 Assembly Y 2400 1200 600 0
4 Assembly Z 2400 2000 1400 1000
Total 9600 6000 3600 2000

Computation of profit
Sl No Particulars Amount
1 Revenue from Product A 16000
2 Revenue from Product B 9000
3 Revenue from Product C 4000
4 Total Revenue 29000
5 Labour Cost
-Product A 3200
-Product B 1800
-Product C 800
Total Cost 5800
6 Material Cost
-Product A 3200
-Product B 1800
-Product C 800
Total Cost 5800
7 Overheads 5000
8 Profit 12400
Part B
The best Product Mix and profit of O’Neil Enterprises using the Constraint method of computation
has been presented here-in-below:
Product Mix based on Profitability- Constraint Method
Sl.
No Particulars
Demand (Per
Week)
Price
(A)
Labour Cost
(B)
Material Cost
(C)
Margin (D=A-B-
C)
1 Product A 80 200 40 40 120
2 Product B 60 150 30 30 90
3 Product C 40 100 20 20 60
4 Product D 20 75 10 10 55
Identification of Bottleneck Factor
Sl No Particulars Product A Product B Product C Product D Total
1 Assembly W 800 600 200 100 1700
2 Assembly X 1200 600 400 100 2300
3 Assembly Y 1200 600 600 100 2500
4 Assembly Z 400 600 400 100 1500

Computation of Profit Margin per Minute on the basis on Bottleneck
Sl No Particulars Product A Product B Product C Product D
1 Profit 120 90 60 55
2 Time taken in Assembly Y 15 10 15 5
3 Profit per Minute 8 9 4 11
4 Rank 3 2 4 1
Allocation of time to products
Sl.
N
o
Particular
s
Min
utes
at
Star
t
Minutes left
after making
20D
Minutes left
after making
60B
Minutes left
after making
80A
Time taken
for 33 unit of
C
Tim
e
left
1
Assembly
W
240
0 2300 1700 900 165 735
2
Assembly
X
240
0 2300 1700 500 330 170
3
Assembly
Y
240
0 2300 1700 500 495 5
4
Assembly
Z
240
0 2300 1700 1300 330 970
960
0 9200 6800 3200
Profitability
Sl No Particulars Amount
1 Revenue from Product A 16000
2 Revenue from Product B 9000
3 Revenue from Product C 3300
4 Revenue from Product D 1500
5 Total Revenue 29800
6 Labour Cost
-Product A 3200
-Product B 1800
-Product C 660
-Product D 200
Total Cost 5660
7 Material Cost
-Product A 3200
-Product B 1800
-Product C 660
-Product D 200
Total Cost 5660
8 Overheads 5000

Profitability
9 Profit 13480
Part C
On comparison of results, it shall be seen that profit is maximised under constraint method. Thus,
constraint method is better than traditional method and serves better allocation of resource to
production.
Answer 2
Part A
Refer Image attached herewith for Precedence Diagram.
Part B
Cycle Time
Output Required (A) 20 Cars per Hour
Time(B) 60 Min
Cycle Time (B/A) 3
Part C
Total Time Taken by all Work Element (A) 13.8
Cycle Time (B) 3
Theoretical Minimum No of Stations (C=A/B) 4.6
5 stations
Part D &E
Refer Excel

PART D

Part E
Task No of Following task
A 7
B 4
C 3
D 2
E 4
F 3
G 3
H 2
I 1
J 2
K 1
L 1
M 0

Station Task Task Time Following Number of Task Remaining Unassigned Time Feasible Remaining Ta
1 A 1.8 7 1.2 B,E
E 0.7 4 0.5 B,E
B 0.4 4 0.1 Idle
2 C 1.6 3 1.4 F,G
G 0.8 3 0.6 F
F 0.5 3 0.1 Idle
3 D 1.5 2 1.5 H,J
H 1.4 2 0.1 Idle none
4 J 1.4 2 1.6 K,L,I
I 1.4 1 0.1 Idle None
5 L 1 1 2 K,M
K 0.5 1 1.5 M
M 0.8 0 0.7 Idle