Operations: Cost Minimization for Meals (Breakfast, Lunch, Dinner)

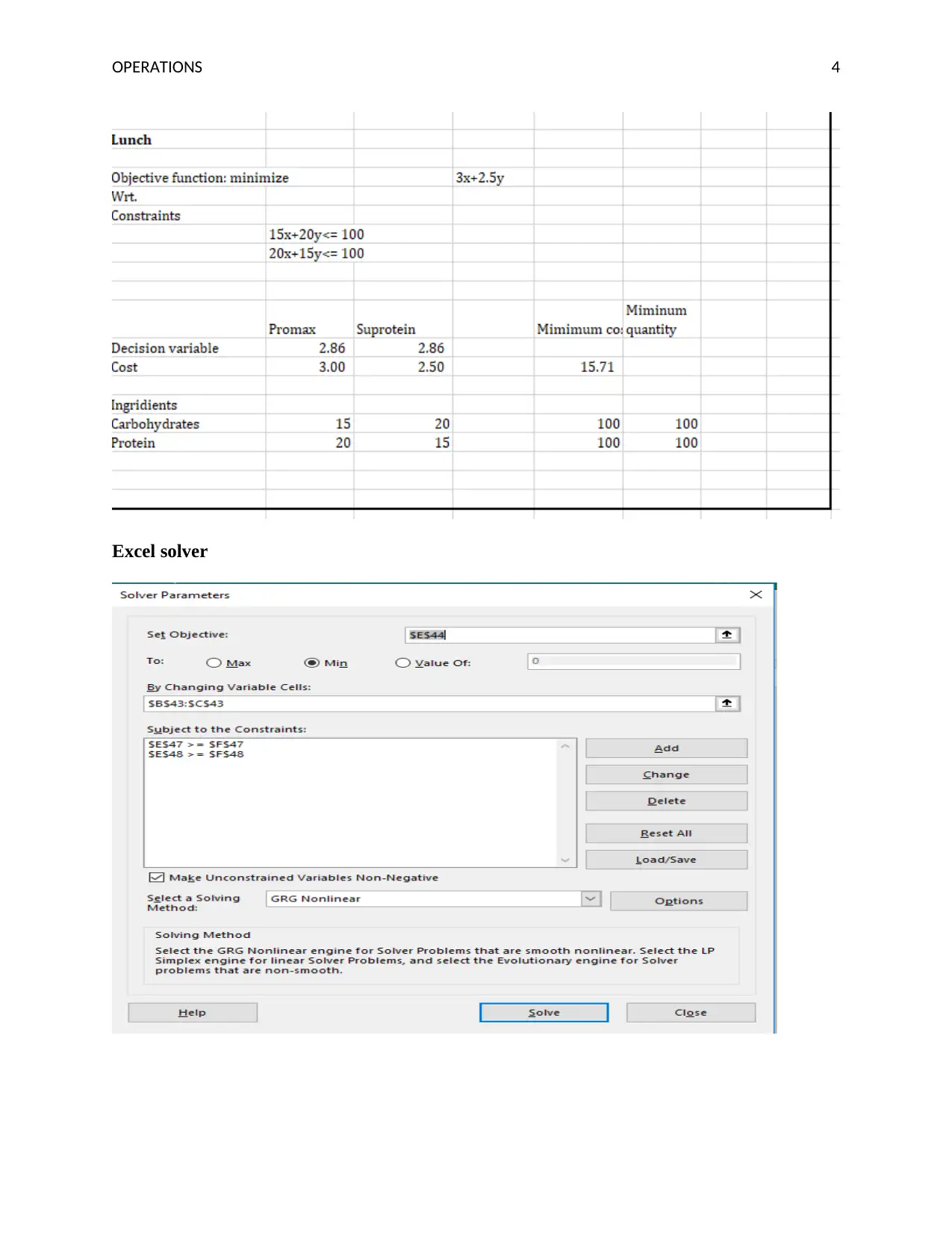
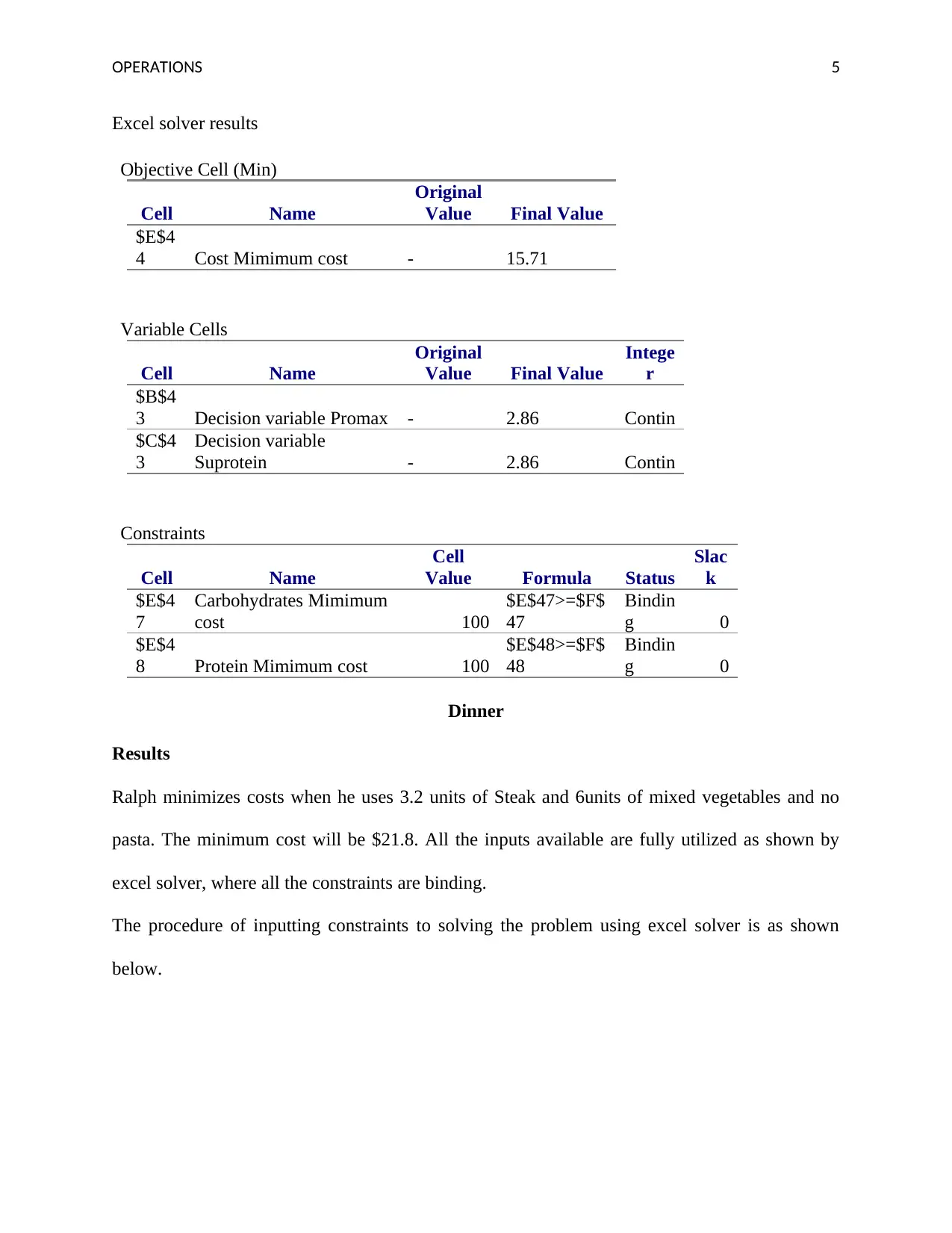
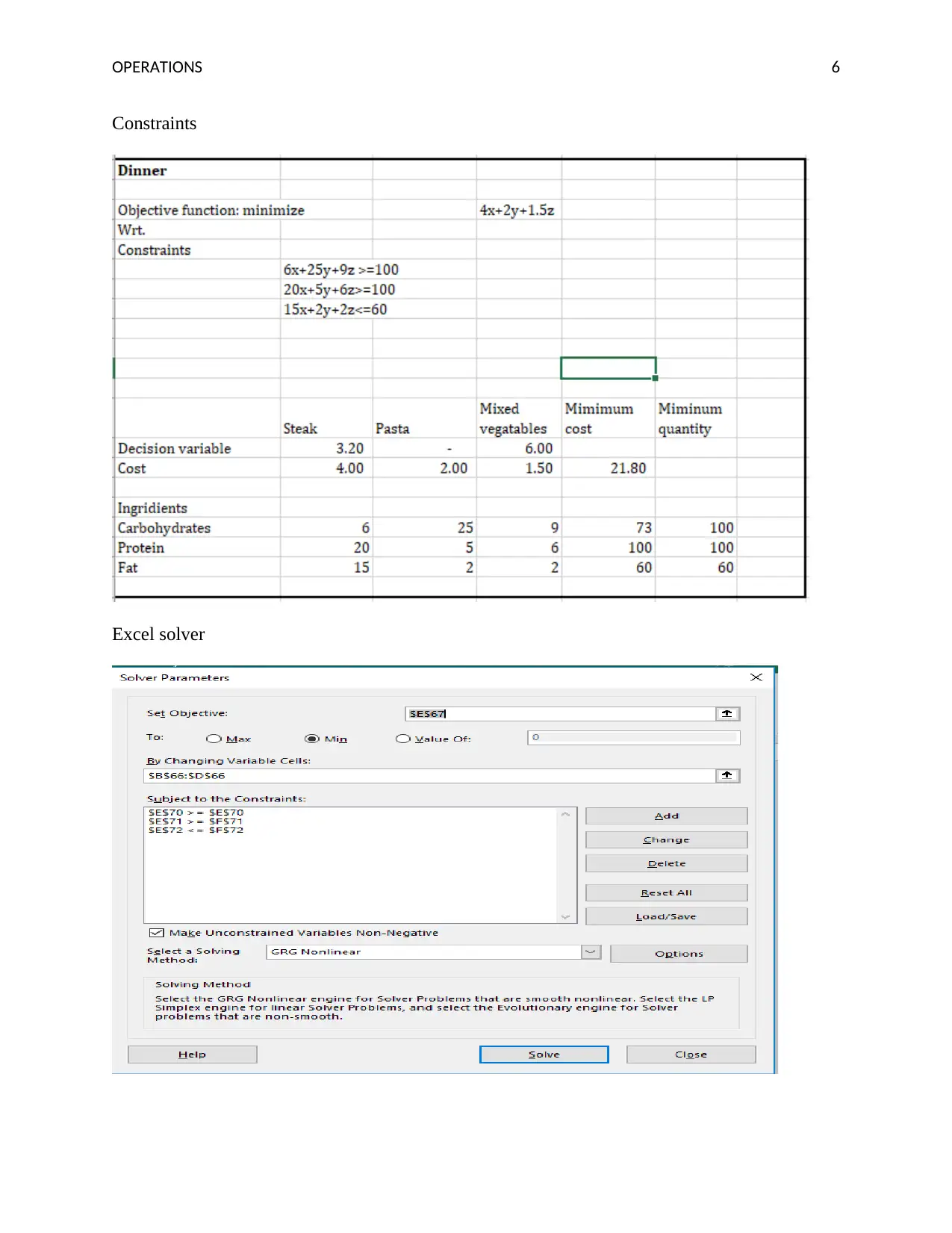
This assignment focuses on operations management principles, specifically cost minimization in meal planning. The student utilizes Excel Solver to determine the most cost-effective combinations of food items for breakfast, lunch, and dinner, considering various constraints such as carbohydrate, protein, and fat requirements. The analysis reveals the optimal quantities of ingredients to minimize the overall meal costs while meeting nutritional needs. The results highlight the use of specific food items to reduce costs. Furthermore, the assignment explores scenarios like the inclusion of previously excluded ingredients (Serious cereal and pasta) by adjusting the maximum cost and the impact of changing protein percentages and ingredient prices on the optimal meal plan. The student also interprets the solver results, including slack variables and binding constraints, to understand the efficiency of each meal plan and the sensitivity of the solution to changes in input parameters.

Running head: OPERATIONS 1
Operations
Student’s Name
Institution Affiliation

OPERATIONS 2
Breakfast
Excel Model and constraints
Excel solver

OPERATIONS 3
Results
Cell Name
Original
Value Final Value
$E$18 contribution Minimum cost 22.31 22.31
Cell Name
Original
Value Final Value Integer
$B$17: $D$17
Cell Name Cell Value Formula Status Slack
$E$21 Constraint 1 Minimum cost 146 $E$21>=$F$21
Not
Binding 46
$E$22 Constraint 2 Minimum cost 100 $E$22>=$F$22 Binding 0
$E$23 Constraint 3 Minimum cost 377 $E$23>=$F$23
Not
Binding 277
$E$24 Constraint 4 Minimum cost 100 $E$24>=$E$24 Binding 0
$E$25 Constraint 5 Minimum cost 331 $E$25>=$F$25
Not
Binding 231
$E$26 Constraint 6 Minimum cost 100 $E$26>=$F$26 Binding 0
$E$27 Constraint 7 Minimum cost 377 $E$27>=$F$27
Not
Binding 277
$E$28 Constraint 8 Minimum cost 146 $E$28>=$F$28
Not
Binding 46
$E$29 Constraint 9 Minimum cost 54 $E$29<=$F$29
Not
Binding 6.153846154
Interpretation
For the breakfast, Ralph should use a combination 4.62 GlanoraMax and 15.38 Muesli-swift to
reduce cost. The minimum cost was estimated to be $22.31.
The slack variables above show additional units that need to be added to each constraint to
transform it into an inequality. For example, constraint1 has a slack of 46 which means that 46
need to be added in the right-hand side of the inequality to transform it into an equation.
Lunch
The results from the excel solver shows that the minimum cost will be realized by utilizing 2.86
units of Promax and 2.86 units of Saprotein. The excel solver results shows that the minimum
cost will be $15.71 and all constraints are binding.
Excel constraints and results

OPERATIONS 4
Excel solver

OPERATIONS 5
Excel solver results
Objective Cell (Min)
Cell Name
Original
Value Final Value
$E$4
4 Cost Mimimum cost - 15.71
Variable Cells
Cell Name
Original
Value Final Value
Intege
r
$B$4
3 Decision variable Promax - 2.86 Contin
$C$4
3
Decision variable
Suprotein - 2.86 Contin
Constraints
Cell Name
Cell
Value Formula Status
Slac
k
$E$4
7
Carbohydrates Mimimum
cost 100
$E$47>=$F$
47
Bindin
g 0
$E$4
8 Protein Mimimum cost 100
$E$48>=$F$
48
Bindin
g 0
Dinner
Results
Ralph minimizes costs when he uses 3.2 units of Steak and 6units of mixed vegetables and no
pasta. The minimum cost will be $21.8. All the inputs available are fully utilized as shown by
excel solver, where all the constraints are binding.
The procedure of inputting constraints to solving the problem using excel solver is as shown
below.

OPERATIONS 6
Constraints
Excel solver

OPERATIONS 7
Excel solver results
Solver Options
Objective Cell (Min)
Cell Name
Original
Value Final Value
$E$6
7 Cost Mimimum cost - 21.80
Variable Cells
Cell Name
Original
Value Final Value
Intege
r
$B$66:$D$66
Constraints
Cell Name Cell Value Formula Status
Slac
k
$E$7
0 Carbohydrates Mimimum cost 73
$E$70>=$E$
70
Bindin
g 0
$E$7
1 Protein Mimimum cost 100
$E$71>=$F$7
1
Bindin
g 0
$E$7
2 Fat Mimimum cost 60
$E$72<=$F$7
2
Bindin
g 0
b) It was noted that for breakfast and dinner, Serious cereal and pasta were eliminated from diet.
In order for these ingredients to be included in the included in the diet, the maximum cost per
serving should be 24.31 for serious meal and 23.8. This value is obtained by adding 1 unit to the
current minimum cost.
c) For protein to be less than 20% it means that the new product can be prepared if and only if
the present constraints holds and the protein in equation 1 is reduced from 146 to 100. The
product should result to reduction of protein price by 20% 46= 9.2

OPERATIONS 8
d) Suprotein is cheaper than Pasta as shown by omission of pasta in minimization cost output. As
a result, it means that a decline in price by half will make the commodity cheaper and this results
to a reduction in cost.