BF360 Operations Research Assignment One - University Name, July 2017

This document presents a comprehensive solution set for an Operations Research assignment (BF360) from July 2017. The assignment covers fundamental concepts in Operations Research, including linear programming, objective functions, constraints, and various solution techniques. The solutions address multiple-choice questions testing the understanding of core principles such as optimal resource utilization, the simplex method, duality, and the graphical approach to solving linear programming problems. The document provides detailed explanations for each question, including step-by-step solutions for problems involving minimization and maximization. It also demonstrates the application of the Gauss-Jordan elimination method. Furthermore, the solutions include model formulations, and optimal solutions to various scenarios involving decision variables, objective functions, and constraints. The assignment's content helps students understand and apply operations research techniques to solve real-world problems.

BF360 - Operations Research Assignment One (July 2017)
Name of the student
Name of the University
Author Note

Q1. The objective of Operations Research is:
c) Optimal utilization of existing resources
Q2. Which technique is used in finding a solution for optimizing a given objective, such as profit
maximization or cost minimization under certain constraints?
d) Linear Programming
Q3. ______________ are the representation of reality
c) Both A and B
Q4. The objective functions and constraints are linear relationships between ______________
d) All the above
Q5. A minimization problem can be converted into a maximization problem by changing the
sign of coefficients in the ______________
b) Objective Functions
Q6. If in a LPP, the solution of a variable can be made infinity large without violating the
constraints, the solution is ______________
b) Unbounded
Q7. Every LPP is associated with another LPP is called ______________
b) Dual
Q8. ______________ assumption means the prior knowledge of all the coefficients in the
objective function, the coefficients of the constraints and the resource values.
b) Certainty
Q9. In Graphical solution of maximisation problem, the line, which we move from origin to the
extreme point of the polygon is:
c) Iso profit line
Q10. The key row indicates
b) Outgoing variable
Q11. Which variables are fictitious and cannot have any physical meaning?
d) None of the above

Q12. Please state which statement is true. (i) All linear programming problems may not have
unique solutions. (ii)The artificial variable technique is a device that gets the starting basic
feasible solution.
a) Both (i) and (ii)
Q13. In which of the following examples can the linear programming technique be used? 1. In
problems where objective functions are linear 2. In assignment problems 3. In getting integer
valued solutions 4. In problems where objective functions are non-linear
a) Options 1, 2 & 3
Q14. Consider the below mentioned statements: 1. The Simplex method optimises the
objective of maximisation or minimisation with the constraints of the new problem. 2. If a
feasible solution is arrived, the optimal value of the new objective function is more than zero.
State True or False:
a) 1-True; 2-Trure
Q15. State whether the following statements are true or false. 1. An LP is in standard form if all
constraints are equality constraints and all variables are nonnegative. 2. Any basic solution in
which all variables are nonnegative is a basic feasible solution (bfs) to the LP.
a) 1-True; 2-Trure
Q16. The simplex method’s rule for choosing the entering basic variable is used because it
always leads to the best adjacent BF solution (largest Z).
False
Q17. The simplex method’s minimum ratio rule for choosing the leaving basic variable is used
because making another choice with a larger ratio would yield a basic solution that is not
feasible.
True
Q18. The graphical approach to solving linear programming problems is limited to models with
up to four decision variables.
False
Q19. Surplus variables may be used to write less-than-or-equal-to constraints in equality form
and slack variables may be used to write greater-than-or-equal-to constraints in equality
False
Q20. If at least one of the basic variables has a coefficient of zero in row 0 of the final tableau,
then the problem has multiple optimal solutions.

False
Q21. If the problem has multiple optimal solutions, then the problem must have a bounded
feasible region.
True
Q22. When a linear programming model has an equality constraint, an artificial variable is
introduced into this constraint in order to start the simplex method with an obvious initial basic
solution that is feasible for the original model.
True
Q23. The reduced cost of a variable is equal to the dual value on the non-negativity constraint
for that variable
True
Q24. Find the optimal solution to the following LP:
Given,
Min z = -x1 – 2x2
Subject to,
2x1 + x2 <= 5
x1 + x2 <= 3
x1, x2 >= 0
In order to solve this problem, let us consider the equality of given to inequality function.
First, we have 2x1 + x2 = 5
Let x1 = 0
Then, we have x2 = 5
Hence, one corner point is (0, 5)
Again, considering x2 = 0, we have,
2x1 = 5
Or, x1 = 2.5
Hence, another point is (2.5, 0)
Thus, it can be said that the equation 2x1 + x2 = 5 will intersect x axis and y axis at (2.5, 0) and
(0, 5) respectively.

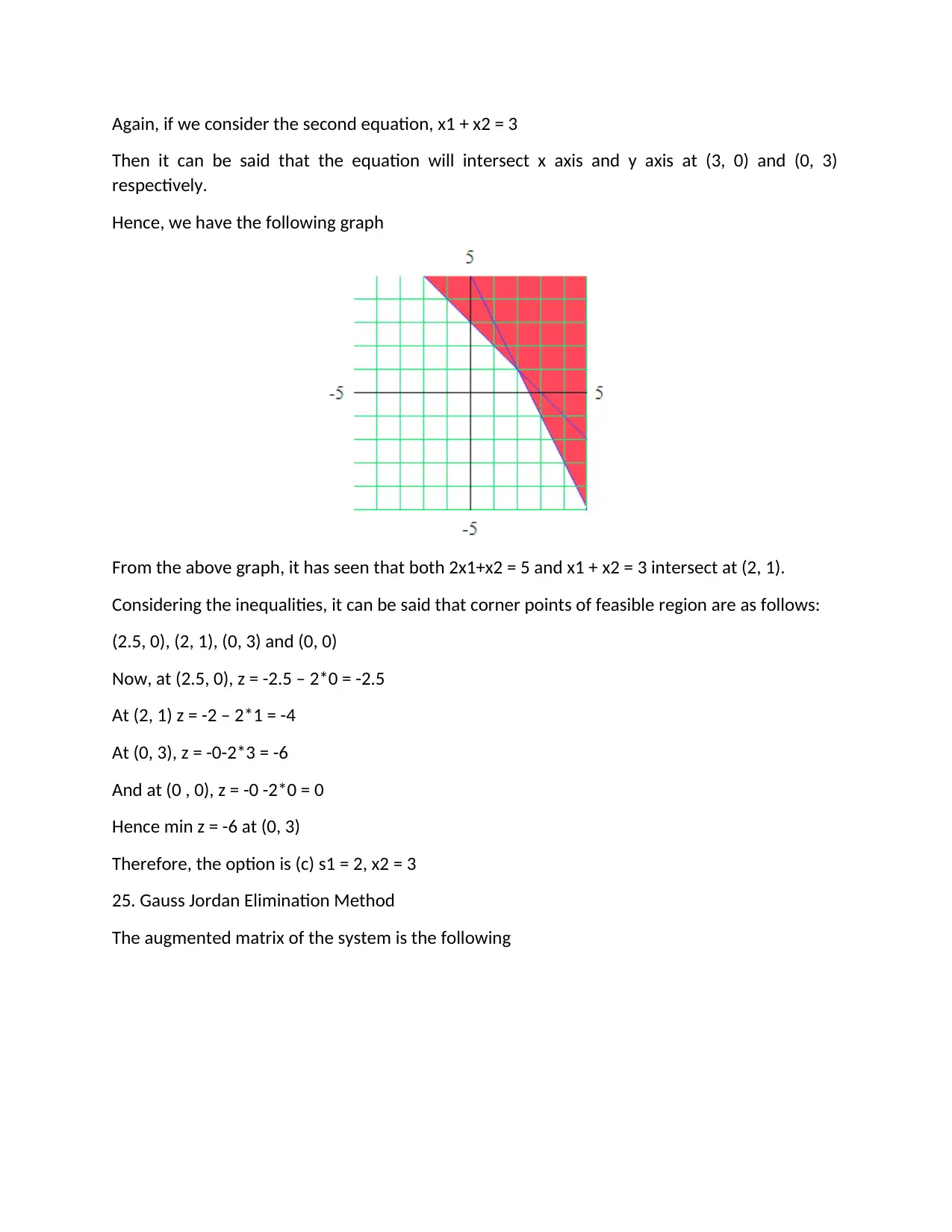
Again, if we consider the second equation, x1 + x2 = 3
Then it can be said that the equation will intersect x axis and y axis at (3, 0) and (0, 3)
respectively.
Hence, we have the following graph
From the above graph, it has seen that both 2x1+x2 = 5 and x1 + x2 = 3 intersect at (2, 1).
Considering the inequalities, it can be said that corner points of feasible region are as follows:
(2.5, 0), (2, 1), (0, 3) and (0, 0)
Now, at (2.5, 0), z = -2.5 – 2*0 = -2.5
At (2, 1) z = -2 – 2*1 = -4
At (0, 3), z = -0-2*3 = -6
And at (0 , 0), z = -0 -2*0 = 0
Hence min z = -6 at (0, 3)
Therefore, the option is (c) s1 = 2, x2 = 3
25. Gauss Jordan Elimination Method
The augmented matrix of the system is the following

Thus the option will be (d) no solution
26. Gauss Jordan Elimination Method
The augmented matrix of the system is the following
Thus the option will be (d) no solution
27. Problem is
Max
Z = 2 x1 + 3 x
2 + 4 x3

subject to
3 x1 + 2 x2 - 3 x3 ≤ 4
2 x1 + 3 x2 + 2 x3 ≤ 6
3 x1 - x2 + 2 x3 ≥ -8
Here b3 = -8 < 0,
so multiply this constraint by -1 to make b3 > 0.
- 3 x1 + x2 - 2 x3 ≤ 8
and x1,x2,x3≥0;
The problem is converted to canonical form by adding slack, surplus and artificial variables as
appropiate
1. As the constraint 1 is of type '≤' we should add slack variable S1
2. As the constraint 2 is of type '≤' we should add slack variable S2
3. As the constraint 3 is of type '≤' we should add slack variable S3
After introducing slack variables
Max
Z = 2 x
1 + 3 x
2 + 4 x3 + 0 S
1 + 0 S2 + 0 S3
subject to
3 x
1 + 2 x
2 - 3 x3 + S1 = 4
2 x
1 + 3 x
2 + 2 x3 + S2 = 6
- 3 x
1 + x
2 - 2 x3 + S3 = 8
and x1,x2,x3,S1,S2,S3≥0

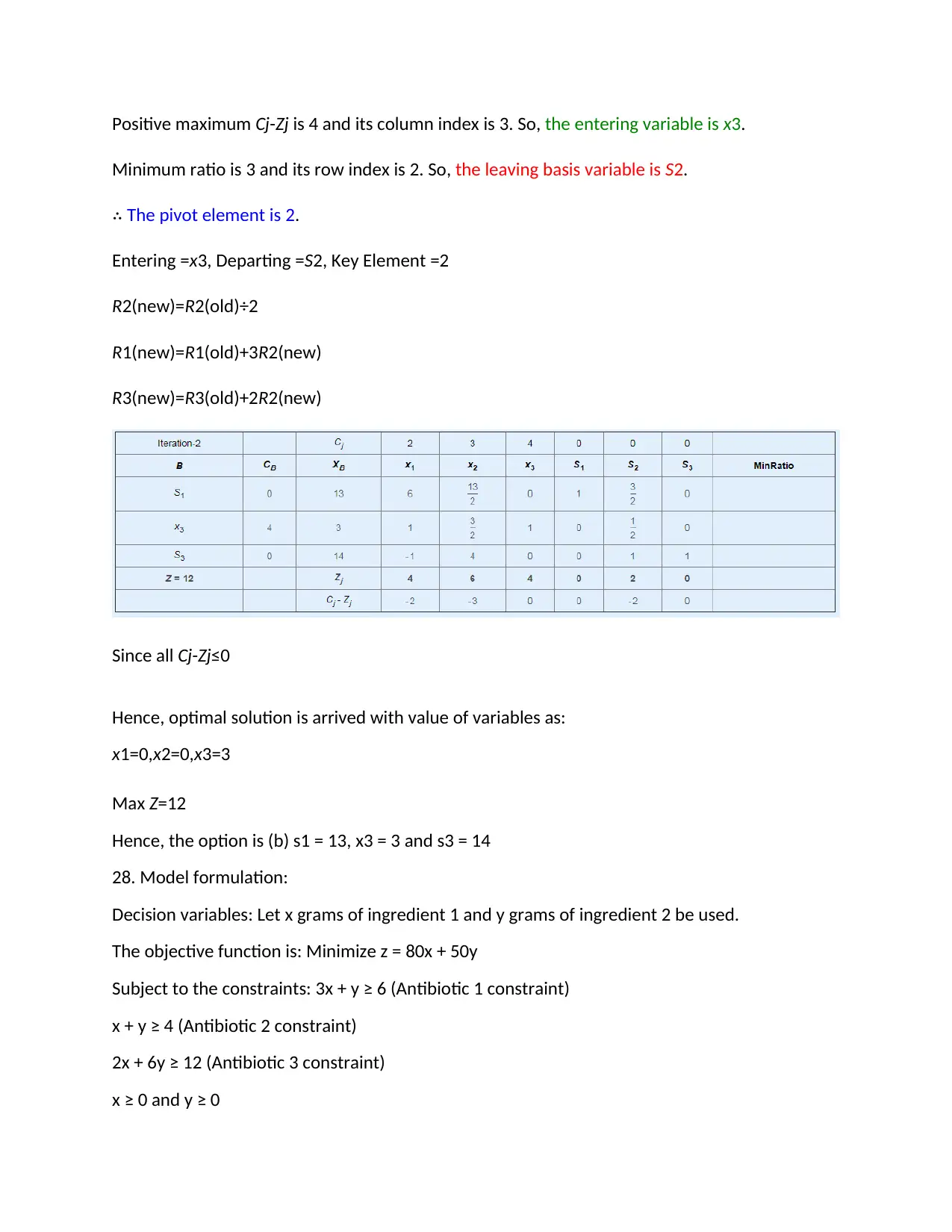
Positive maximum Cj-Zj is 4 and its column index is 3. So, the entering variable is x3.
Minimum ratio is 3 and its row index is 2. So, the leaving basis variable is S2.
∴ The pivot element is 2.
Entering =x3, Departing =S2, Key Element =2
R2(new)=R2(old)÷2
R1(new)=R1(old)+3R2(new)
R3(new)=R3(old)+2R2(new)
Since all Cj-Zj≤0
Hence, optimal solution is arrived with value of variables as:
x1=0,x2=0,x3=3
Max Z=12
Hence, the option is (b) s1 = 13, x3 = 3 and s3 = 14
28. Model formulation:
Decision variables: Let x grams of ingredient 1 and y grams of ingredient 2 be used.
The objective function is: Minimize z = 80x + 50y
Subject to the constraints: 3x + y ≥ 6 (Antibiotic 1 constraint)
x + y ≥ 4 (Antibiotic 2 constraint)
2x + 6y ≥ 12 (Antibiotic 3 constraint)
x ≥ 0 and y ≥ 0

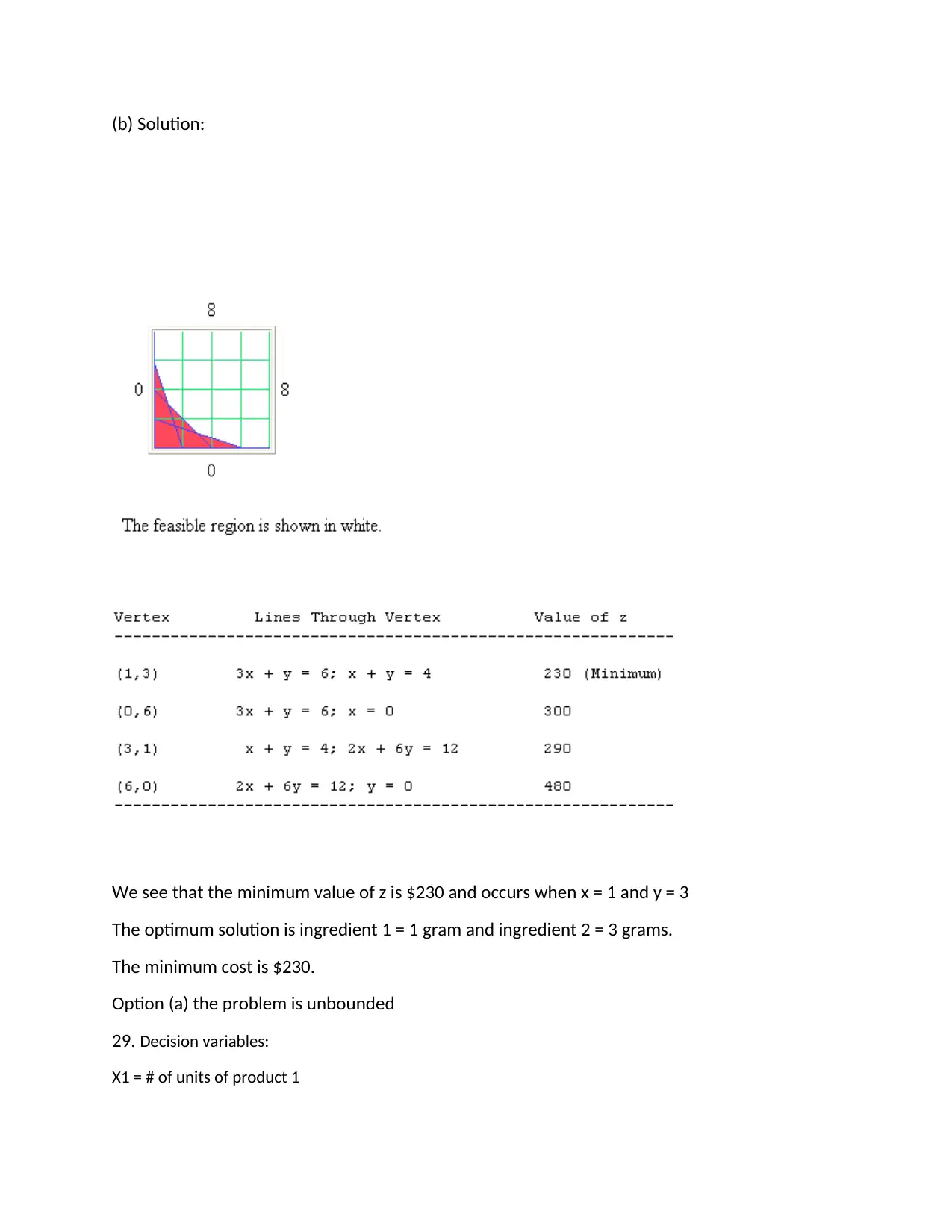
(b) Solution:
We see that the minimum value of z is $230 and occurs when x = 1 and y = 3
The optimum solution is ingredient 1 = 1 gram and ingredient 2 = 3 grams.
The minimum cost is $230.
Option (a) the problem is unbounded
29. Decision variables:
X1 = # of units of product 1

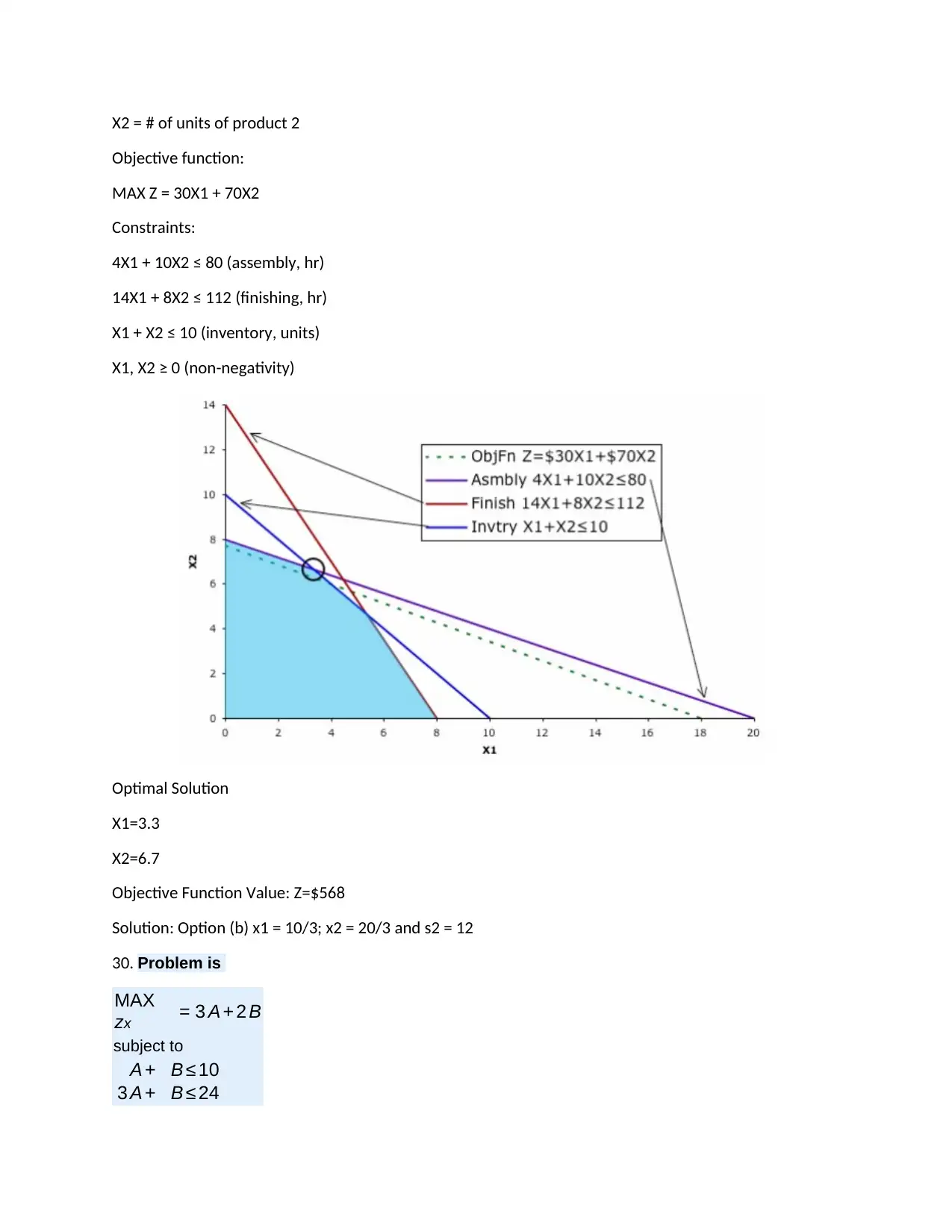
X2 = # of units of product 2
Objective function:
MAX Z = 30X1 + 70X2
Constraints:
4X1 + 10X2 ≤ 80 (assembly, hr)
14X1 + 8X2 ≤ 112 (finishing, hr)
X1 + X2 ≤ 10 (inventory, units)
X1, X2 ≥ 0 (non-negativity)
Optimal Solution
X1=3.3
X2=6.7
Objective Function Value: Z=$568
Solution: Option (b) x1 = 10/3; x2 = 20/3 and s2 = 12
30. Problem is
MAX
zx = 3 A + 2 B
subject to
A + B ≤ 10
3 A + B ≤ 24

A + 2 B ≤ 16
B ≥ 0
and A,B≥0;
1. To draw constraint A+B≤10→(1)
Treat it as A+B=10
When A=0 then B=?
⇒(0)+B=10
⇒B=10
When B=0 then A=?
⇒A+(0)=10
⇒A=10
A 0 10
B 10 0
2. To draw constraint 3A+B≤24→(2)
Treat it as 3A+B=24
When A=0 then B=?
⇒3(0)+B=24
⇒B=24
When B=0 then A=?
⇒3A+(0)=24
⇒3A=24
⇒A=243=8
A 0 8
B 24 0
3. To draw constraint A+2B≤16→(3)

Treat it as A+2B=16
When A=0 then B=?
⇒(0)+2B=16
⇒2B=16
⇒B=162=8
When B=0 then A=?
⇒A+2(0)=16
⇒A=16
A 0 16
B 8 0
4. To draw constraint B≥0→(4)
Treat it as B=0
Here line is parallel to X-axis
A 0 1
B 0 0