Finite Math Unit 3 Project: Optimizing Cookie Production

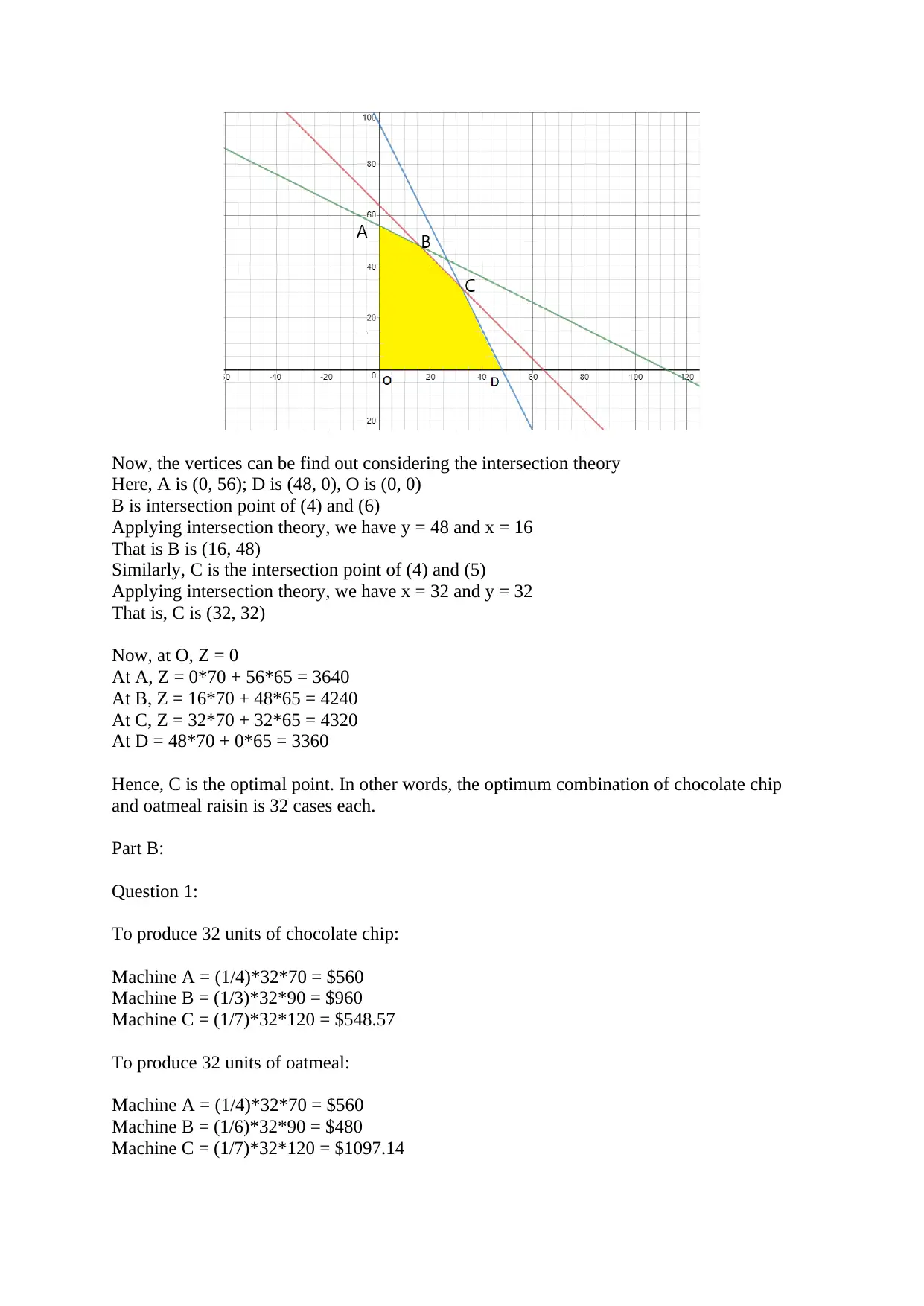
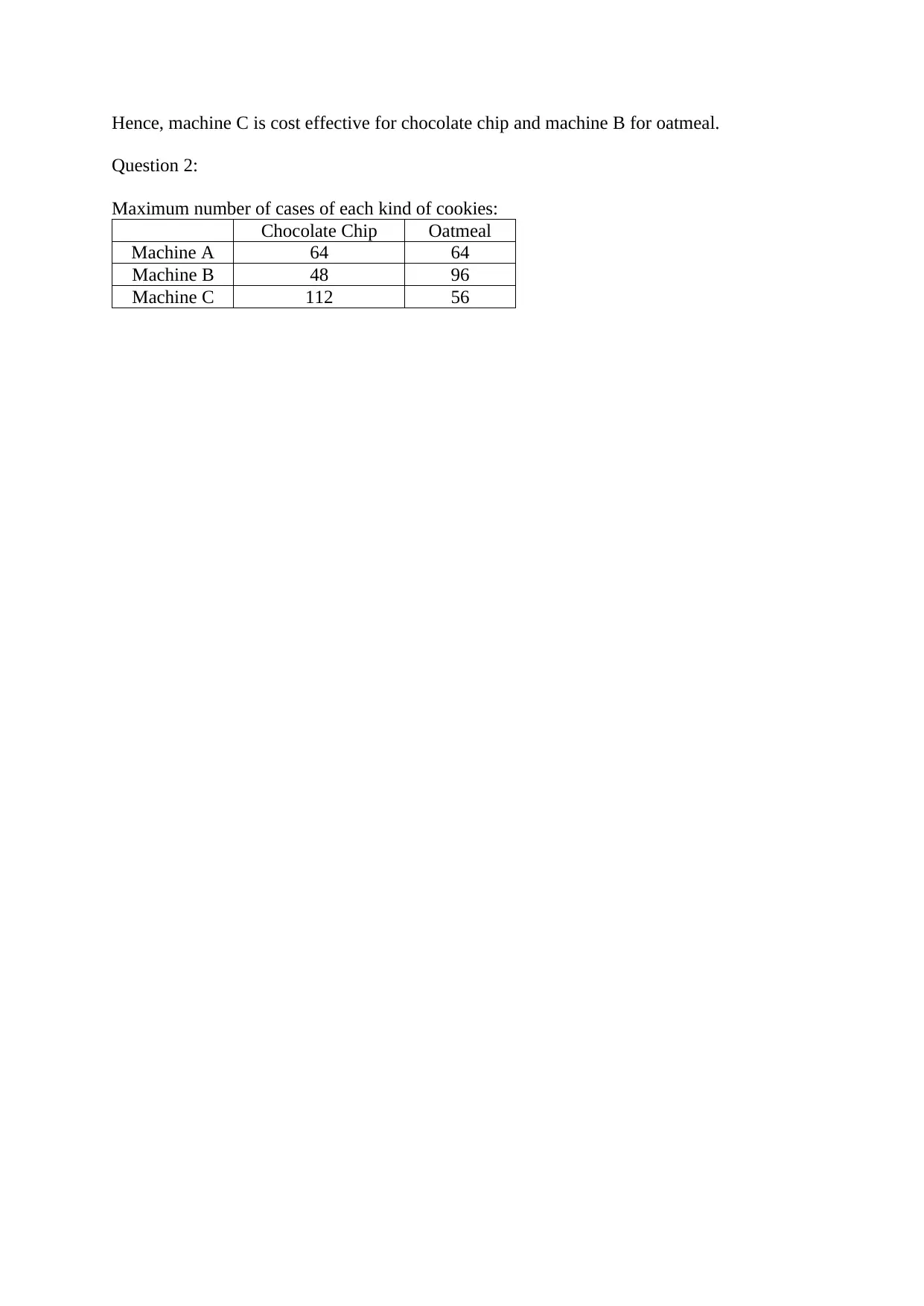
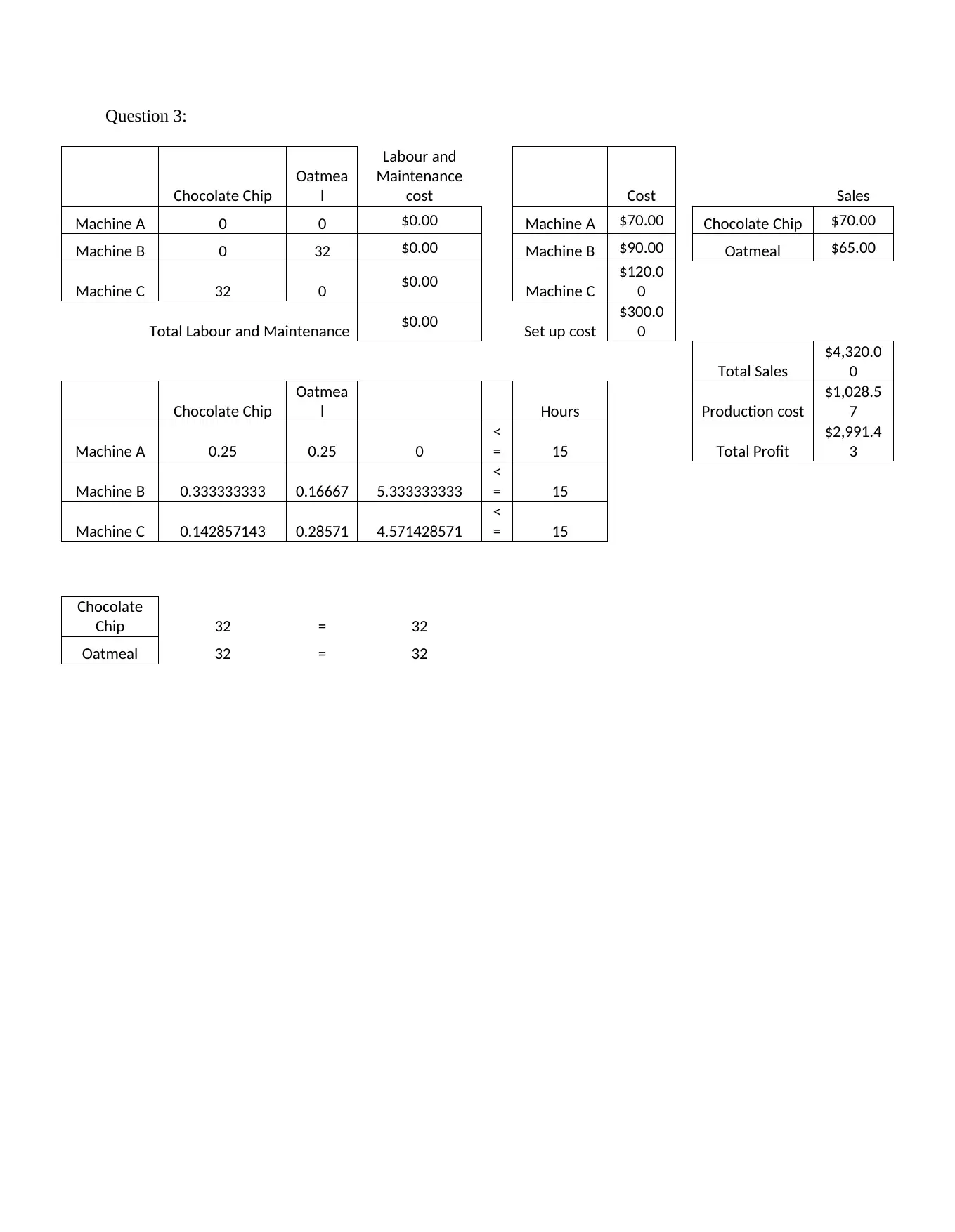
This project analyzes a cookie production scenario using linear programming to maximize revenue. The student formulates an objective function to maximize total sales based on the selling prices of chocolate chip and oatmeal raisin cookies, subject to constraints imposed by the production capacity of three machines (A, B, and C). The problem is solved graphically, identifying the feasible region and optimal solution through the analysis of vertices. Part A defines the Linear Programming Problem (LPP) and its constraints and objective function. Part B delves into cost analysis, determining cost-effectiveness for each cookie type per machine, calculating maximum production quantities, and analyzing labor, maintenance, and setup costs. The project concludes by determining the optimal production levels of each cookie type to maximize profit, with a detailed breakdown of costs and sales, demonstrating a strong grasp of linear programming principles and their practical application in business decision-making. The assignment includes a bibliography with sources on linear programming.

Finite Math – Unit 3 Project
Name of the Student
Name of the University
Author Note

Part A:
Let X denotes the number of cases of chocolate chip, and y be the number of cases of oatmeal
raisin.
Given the chocolate chip cookies sell for $70 per case, and the oatmeal raisin cookies sell for
$65 per case.
Hence, total sales revenue is 70*X + 65*Y
Therefore, the objective function will be
Max Z = 70*X + 65*Y
As mentioned, the plant has three machines such as Machine A, Machine B and Machine C.
Considering the time required to produce each type of cookies, following are the constraints:
For machine A: (1/4)*X + (1/4)*Y <= 16
Or, X + Y <= 64 ……… (1)
For machine B: (1/3)*X + (1/6)*Y <= 16
Or, 2X + Y <= 96 …….. (2)
For machine C: (1/7)*X + (2/7)*Y <= 16
Or, X + 2Y <= 112 ……. (3)
Hence, the LPP will look like
Max Z = 70X + 65Y
Subject to
X + Y <= 64 ……… (1)
2X + Y <= 96 …….. (2)
X + 2Y <= 112 ……. (3)
X, Y >= 0
Now, to solve this problem using graph, first we have to convert all in-equality as equations
From (1), we have
X + Y = 64 …….. (4)
Putting, X = 0, we have Y = 64; similarly putting Y = 0, we have X = 64
Hence, equation (4) will intersect y-axis and x-axis at (0, 64) and (64, 0) respectively.
From (2), we have
2X + Y = 96 …….. (5)
Putting, X = 0, we have Y = 96; similarly putting Y = 0, we have X = 48
Hence, equation (5) will intersect y-axis and x-axis at (0, 96) and (48, 0) respectively.
From (3), we have
X + 2Y = 112 …….. (6)
Putting, X = 0, we have Y = 56; similarly putting Y = 0, we have X = 112
Hence, equation (6) will intersect y-axis and x-axis at (0, 56) and (112, 0) respectively.
Now, plotting these equations into graph, we have the feasible region as OABCDO

Now, the vertices can be find out considering the intersection theory
Here, A is (0, 56); D is (48, 0), O is (0, 0)
B is intersection point of (4) and (6)
Applying intersection theory, we have y = 48 and x = 16
That is B is (16, 48)
Similarly, C is the intersection point of (4) and (5)
Applying intersection theory, we have x = 32 and y = 32
That is, C is (32, 32)
Now, at O, Z = 0
At A, Z = 0*70 + 56*65 = 3640
At B, Z = 16*70 + 48*65 = 4240
At C, Z = 32*70 + 32*65 = 4320
At D = 48*70 + 0*65 = 3360
Hence, C is the optimal point. In other words, the optimum combination of chocolate chip
and oatmeal raisin is 32 cases each.
Part B:
Question 1:
To produce 32 units of chocolate chip:
Machine A = (1/4)*32*70 = $560
Machine B = (1/3)*32*90 = $960
Machine C = (1/7)*32*120 = $548.57
To produce 32 units of oatmeal:
Machine A = (1/4)*32*70 = $560
Machine B = (1/6)*32*90 = $480
Machine C = (1/7)*32*120 = $1097.14

Hence, machine C is cost effective for chocolate chip and machine B for oatmeal.
Question 2:
Maximum number of cases of each kind of cookies:
Chocolate Chip Oatmeal
Machine A 64 64
Machine B 48 96
Machine C 112 56

Question 3:
Chocolate Chip
Oatmea
l
Labour and
Maintenance
cost Cost Sales
Machine A 0 0 $0.00 Machine A $70.00 Chocolate Chip $70.00
Machine B 0 32 $0.00 Machine B $90.00 Oatmeal $65.00
Machine C 32 0 $0.00 Machine C
$120.0
0
Total Labour and Maintenance $0.00 Set up cost
$300.0
0
Total Sales
$4,320.0
0
Chocolate Chip
Oatmea
l Hours Production cost
$1,028.5
7
Machine A 0.25 0.25 0
<
= 15 Total Profit
$2,991.4
3
Machine B 0.333333333 0.16667 5.333333333
<
= 15
Machine C 0.142857143 0.28571 4.571428571
<
= 15
Chocolate
Chip 32 = 32
Oatmeal 32 = 32

Bibliography
Dantzig, G., 2016. Linear programming and extensions. Princeton university press.
Vanderbei, R.J., 2015. Linear programming. Heidelberg: Springer.
Vielma, J.P., 2015. Mixed integer linear programming formulation techniques. Siam Review, 57(1), pp.3-
57.