Optimization Problems Assignment Solution - Economics Course

This document presents a comprehensive solution to an optimization assignment, addressing various problems related to linear programming and optimization techniques. The solution begins by determining feasibility of points based on given constraints, followed by graphical analysis of linear programming problems to identify feasible regions and optimal solutions. The assignment also explores the linear programming theorem and its implications, the concept of unboundedness in both maximization and minimization problems, and the development of mathematical models for production processes and profit maximization. The solution includes detailed calculations, graphical representations, and interpretations to arrive at optimal solutions for each problem. Finally, the solution covers a cheese blending problem, formulating a linear programming model to determine the optimal blend of cheese to maximize profit, considering various constraints and costs.

Running head: OPTIMIZATION 1
Optimization
Name
Institution

OPTIMIZATION 2
Optimization
Problem 1
Part a
Let x1=number of corn acres∧x2 =number of acres withwheat
Weekly revenues=( 3× 10) x1+(4 ×25)x2 ¿ 30 x1 +100 x2
The objective function is: Maximize Z ¿ 30 x1+100 x2
The constraints are:
Total land available constraint : x1 + x2 ≤ 7
Total labour hours available constraint : 4 x1+10 x2 ≤ 40
The minimum bushel of corn constraint :10 x1 ≥ 30
x1 , x2 ≥ 0(sign restriction)
Part b
x1=2 , x2=3
land available constraint : x1 +x2 ≤ 7 →2+3=5 ≤7 ( constraint satisfied )
labour hours constraint : 4 x1+10 x2 ≤ 4 0 → 4 ( 2 ) +10 ( 3 ) =38 ≤ 40(satisfied )
bushel of corn constraint :10 x1 ≥ 3 0→ 10 ( 2 ) =20<30 (not satisfied)
Hence the point x1=2 , x2=3 is not in the feasible region.

OPTIMIZATION 3
Part c
x1=4 , x2=2
land available constraint : x1 +x2 ≤ 7 → 4+2=6 ≤7 ( constraint satisfied )
labour hours constraint : 4 x1+10 x2 ≤ 4 0 → 4 ( 4 ) +10 ( 2 )=36 ≤ 40(satisfied )
bushel of corn constraint :10 x1 ≥ 3 0→ 10 ( 4 )=40≥ 30( satisfied )
Hence the point x1=4 , x2=2 is in the feasible region since it satisfies all constraints
Part d
x1=2 , x2=−1
The point is not in the feasible region since x2=−1 does not satisfy the non-negativity constraint.
Part e
x1=3 , x2 =2
land available constraint : x1 +x2 ≤ 7 →3+2=5 ≤7 ( constraint satisfied )
labour hours constraint : 4 x1+10 x2 ≤ 4 0 → 4 ( 3 ) +10 ( 2 )=32 ≤ 40(satisfied )
bushel of corn constraint :10 x1 ≥ 3 0→ 10 ( 3 )=3 0 ≥ 3 0( satisfied)
Hence the point x1=3 , x2 =2 is in the feasible region.

OPTIMIZATION 4
Part f
Let x1=corn bushels∧x2=wheat bushels
corn acres= corn bushels
production per corn acre = x1
10 =0.1 x1
wheat acres= wheat bushels
production per wheat acre = x2
25 =0.04 x2
Labour hours ( corn ) =labour hours per acre × number of acres=4 ( 0.1 x1 ) =0. 4 x1
Labour hours ( wheat ) =labour hours per acre × number of acres=10 ( 0.04 x2 ) =0.4 x2
Weekly revenues=(3× x1
10 )+(4 × x2
25 )¿ 0.3 x1+0.16 x2
The objective function is: Maximize Z ¿ 0.3 x1 +0.16 x2
The constraints are:
Total land available constraint :0.1 x1 +0.04 x2 ≤ 7
Total labour hours available constraint : 0.4 x1 +0.4 x2 ≤ 40
The minimum bushel of corn constraint : x1 ≥ 30
x1 , x2 ≥ 0(sign restriction)
Part g

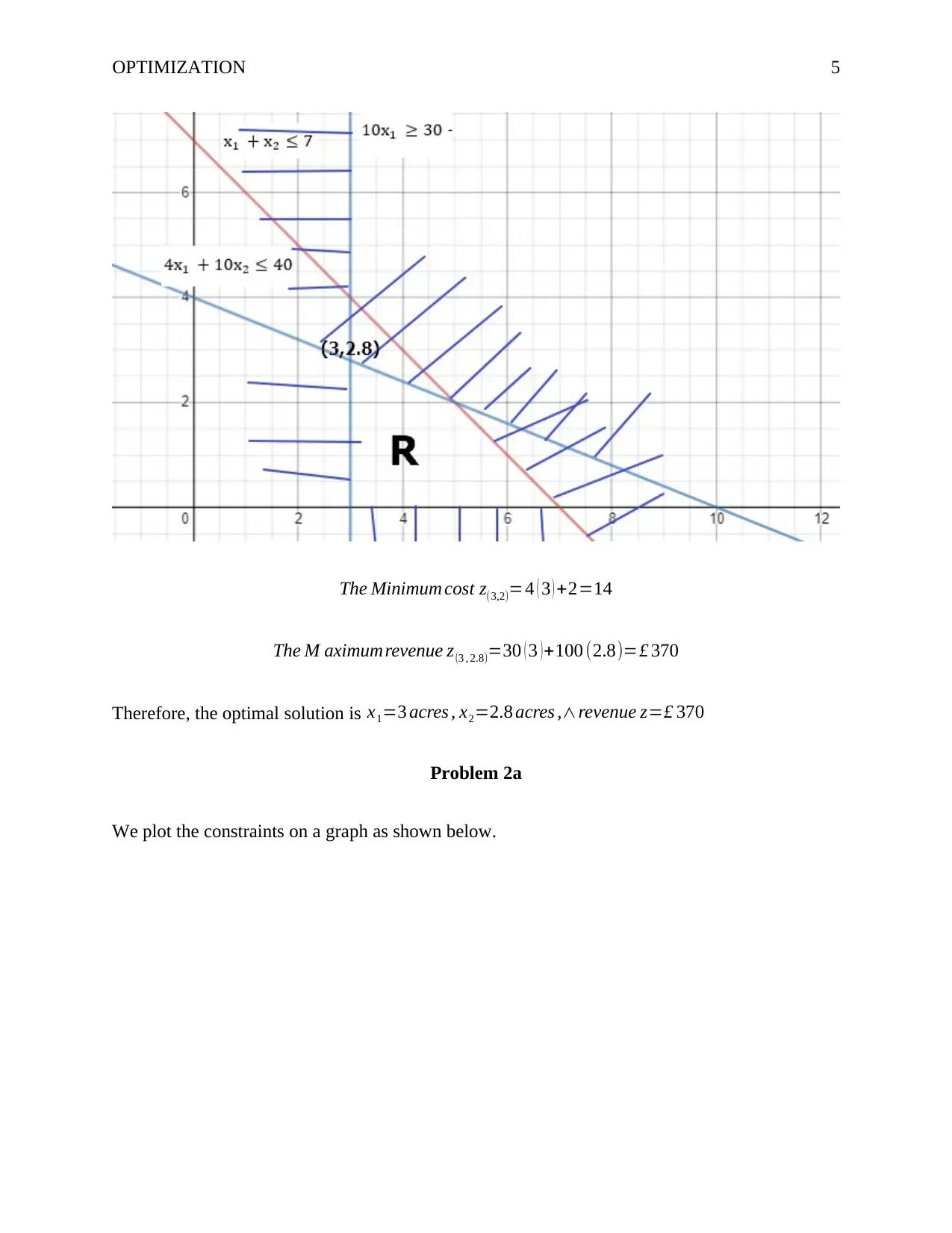
OPTIMIZATION 5
The Minimum cost z(3,2)=4 ( 3 ) +2=14
The M aximumrevenue z(3 , 2.8)=30 ( 3 )+100 (2.8)=£ 370
Therefore, the optimal solution is x1=3 acres , x2=2.8 acres ,∧revenue z=£ 370
Problem 2a
We plot the constraints on a graph as shown below.

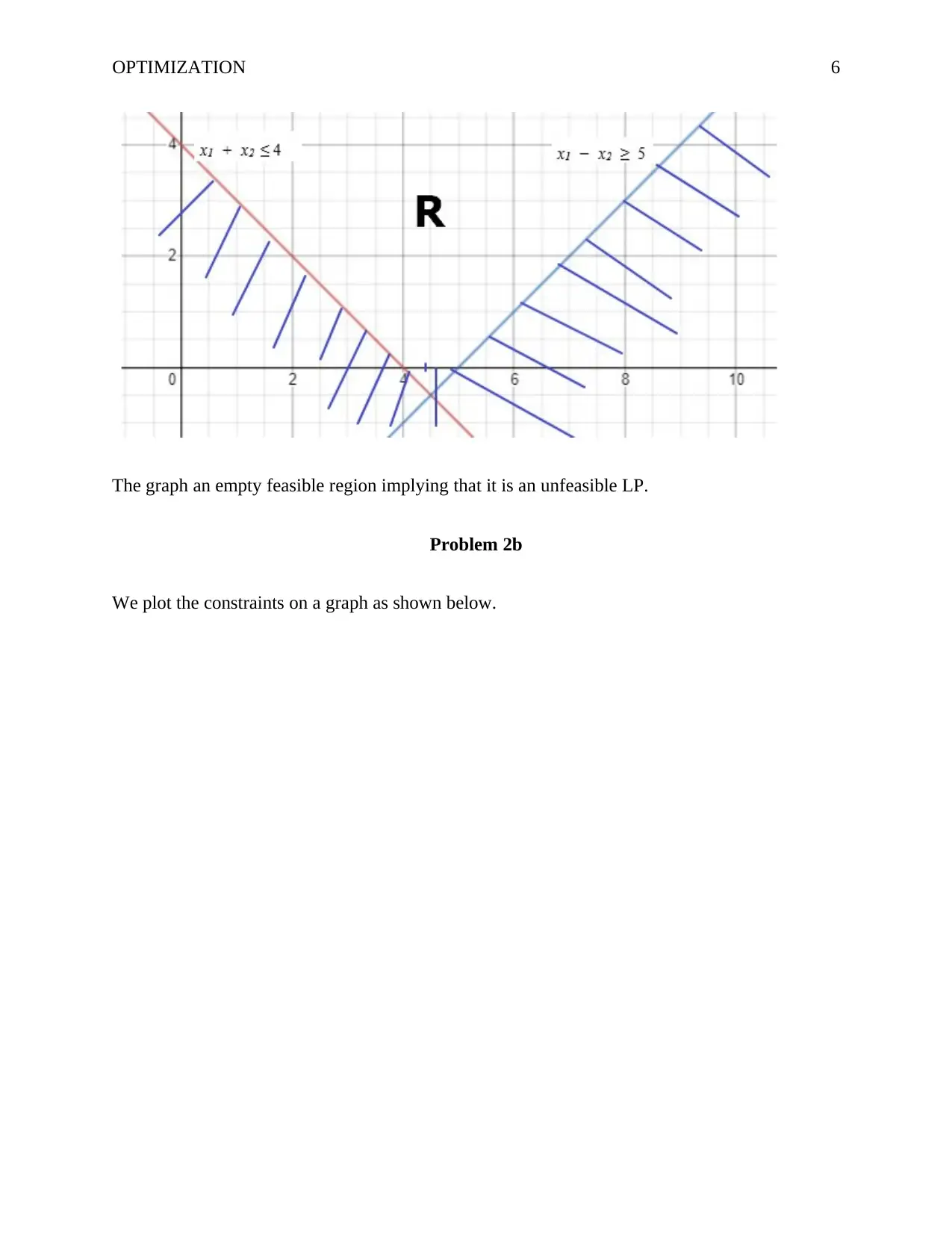
OPTIMIZATION 6
The graph an empty feasible region implying that it is an unfeasible LP.
Problem 2b
We plot the constraints on a graph as shown below.

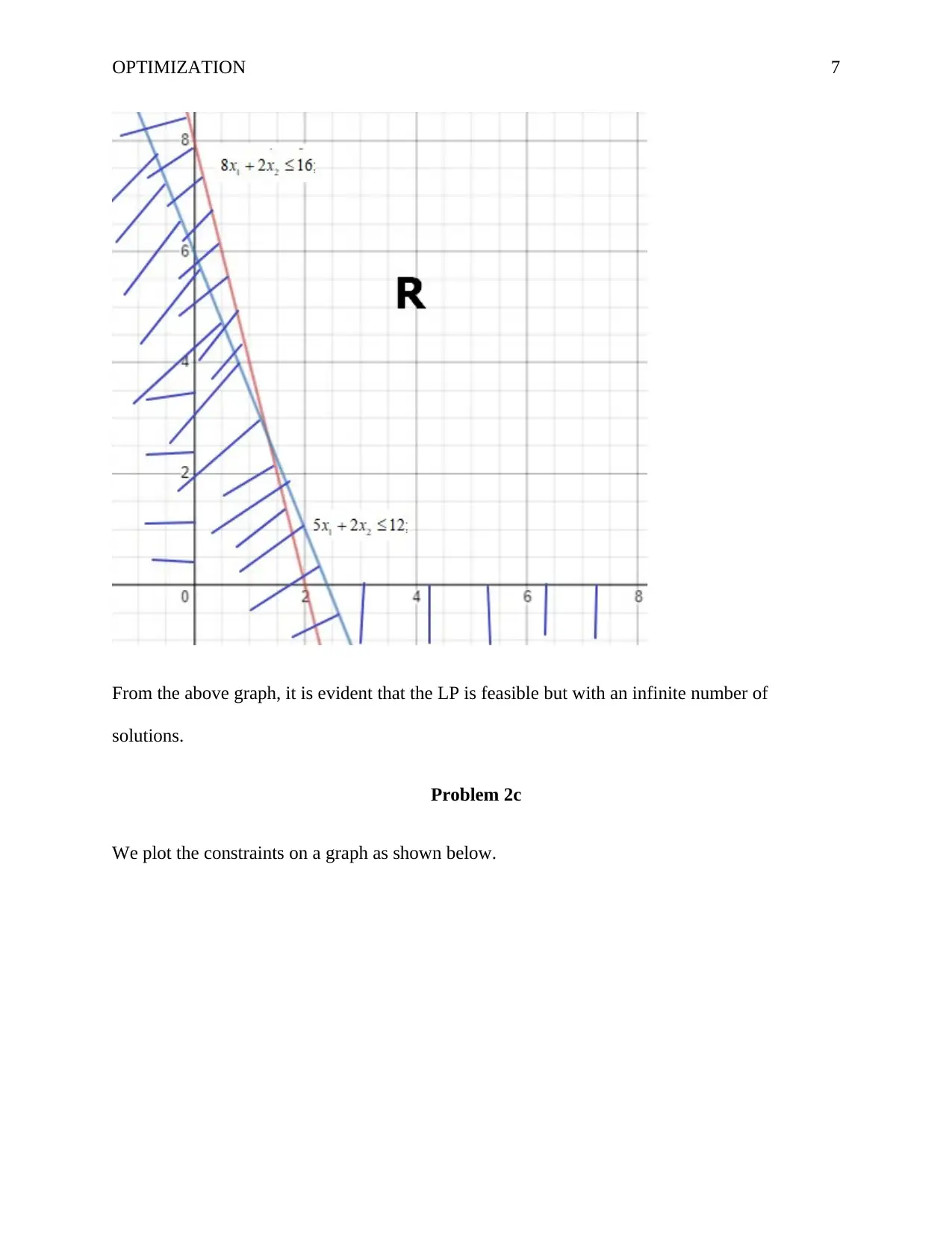
OPTIMIZATION 7
From the above graph, it is evident that the LP is feasible but with an infinite number of
solutions.
Problem 2c
We plot the constraints on a graph as shown below.

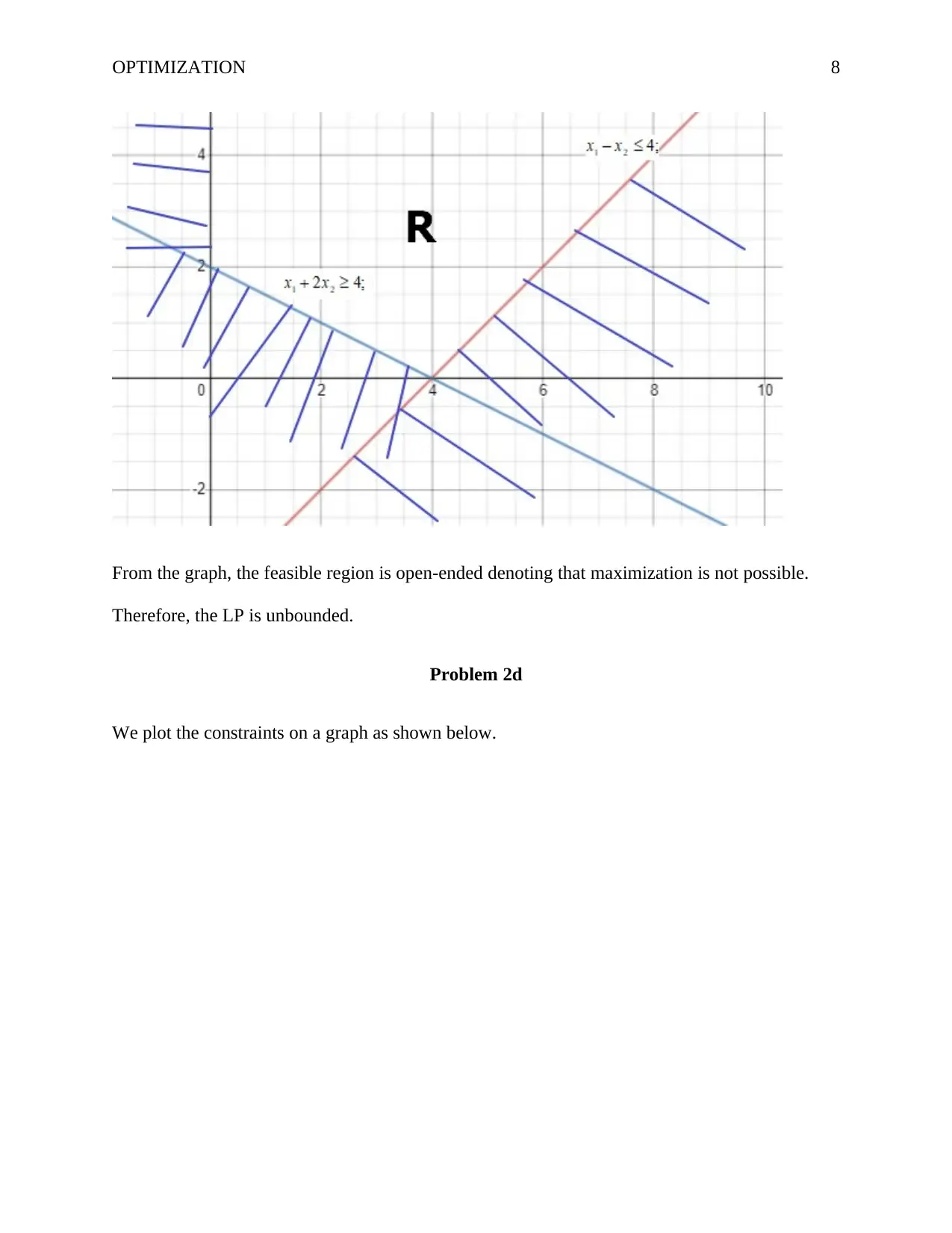
OPTIMIZATION 8
From the graph, the feasible region is open-ended denoting that maximization is not possible.
Therefore, the LP is unbounded.
Problem 2d
We plot the constraints on a graph as shown below.

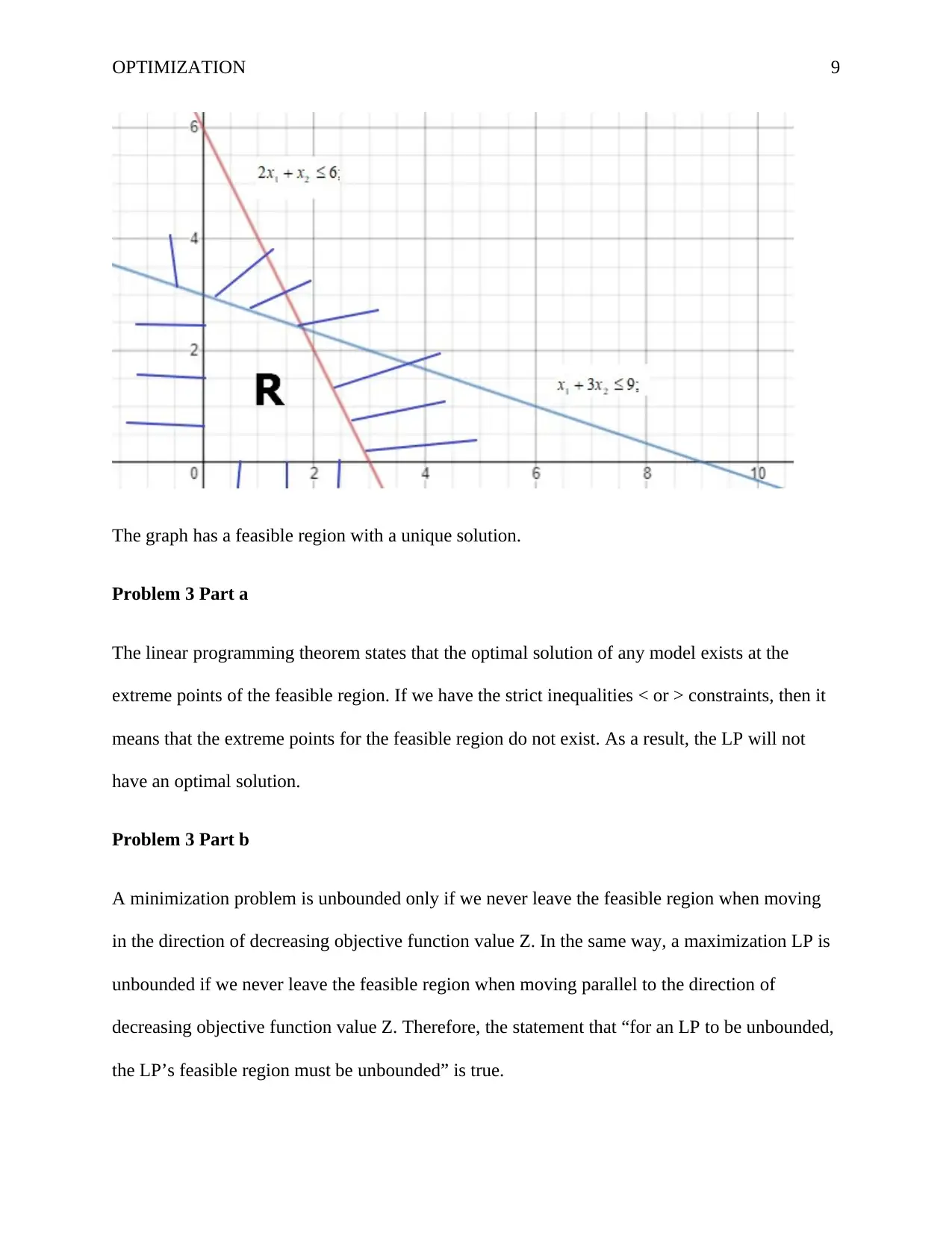
OPTIMIZATION 9
The graph has a feasible region with a unique solution.
Problem 3 Part a
The linear programming theorem states that the optimal solution of any model exists at the
extreme points of the feasible region. If we have the strict inequalities < or > constraints, then it
means that the extreme points for the feasible region do not exist. As a result, the LP will not
have an optimal solution.
Problem 3 Part b
A minimization problem is unbounded only if we never leave the feasible region when moving
in the direction of decreasing objective function value Z. In the same way, a maximization LP is
unbounded if we never leave the feasible region when moving parallel to the direction of
decreasing objective function value Z. Therefore, the statement that “for an LP to be unbounded,
the LP’s feasible region must be unbounded” is true.

OPTIMIZATION 10
Problem 3 Part c
In a maximization problem, there exists points with arbitrary large Z values in the feasible
region. Similarly, there exists arbitrary small values of Z in the feasible region of a minimization
problem. The scenario denotes that an unbounded solution should not occur when the LP is
modelled in the right way. Hence, the statement is false.
Problem 4
A, B, and C are variables that represent the 3 chemicals produced through 2 processes
Let x1∧x2 be the two production processes.
The cost per hour =4 x1 + x2
The object function is¿ minimize the cost , z=4 x ¿1 + x2
The inequality constraints are:
Chemical A :3 x1+ x2 ≥10 units
Chemical B : x1 +x2 ≥ 5 units
Chemical C :1 x1+0 x2 ≥3 units → x1 ≥3 units
x1 , x2 ≥ 0( sign restriction)
We convert each inequality constraint into an equality to get:
3 x1+x2=10 units
x1+ x2=5units

OPTIMIZATION 11
x1=3 units
Then, we find two coordinate points for each equality constraint for drawing the graph.
Equality constraint 1: 3 x1+x2=10 units
Point 1 Point 2
x1 0 3
x2 10 1
Equality constraint 2: x1+ x2=5units
Point 1 Point 2
x1 0 5
x2 5 0
x1=3 is a vertical line cutting through the x-axis at the point (3,0).
We plot the points on the graph and identify the feasible region.

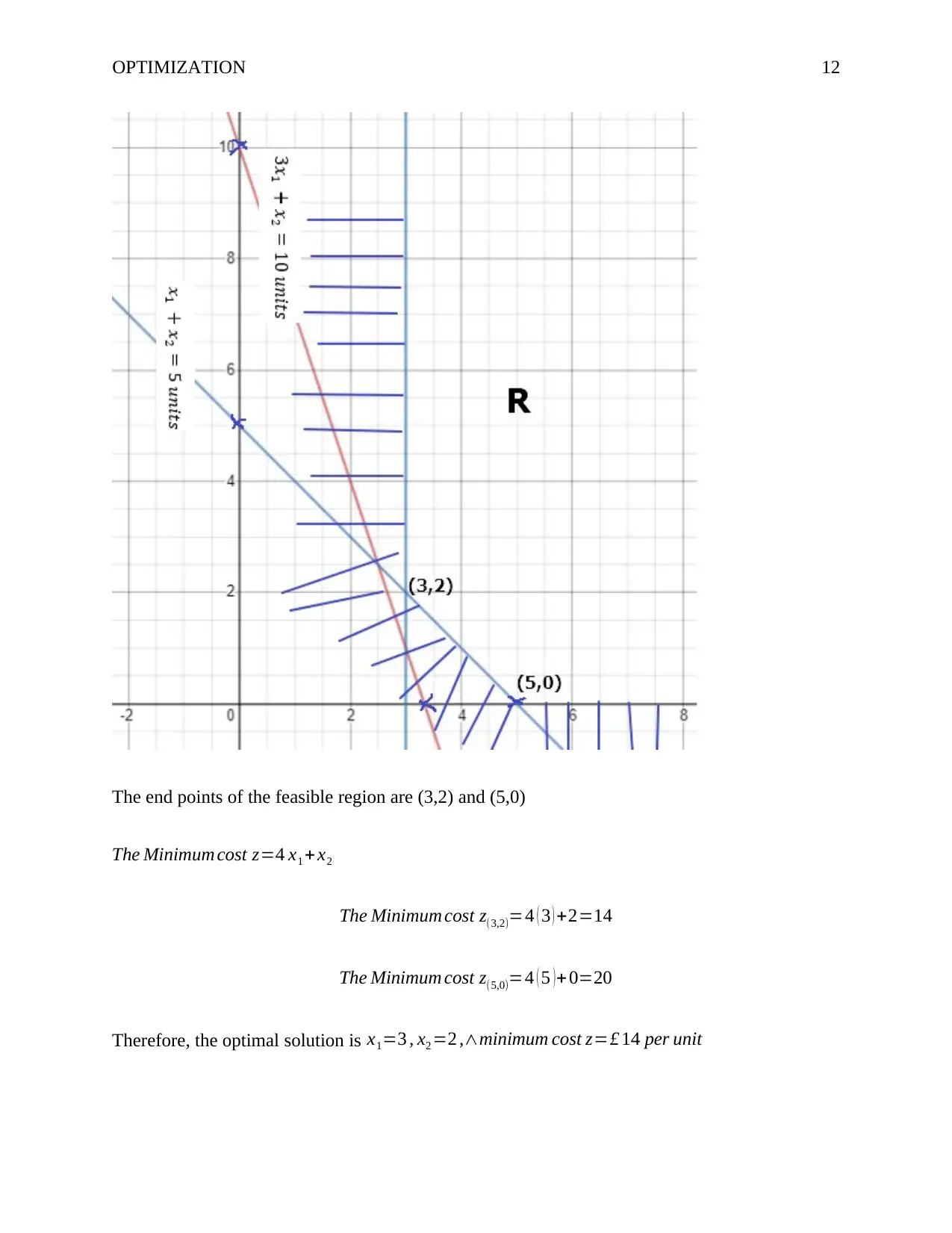
OPTIMIZATION 12
The end points of the feasible region are (3,2) and (5,0)
The Minimum cost z=4 x1 + x2
The Minimum cost z(3,2)=4 ( 3 ) +2=14
The Minimum cost z(5,0)=4 ( 5 )+ 0=20
Therefore, the optimal solution is x1=3 , x2 =2 ,∧minimum cost z=£ 14 per unit