Analysis of Orthogonal Matrices, Eigenvalues, and Quadratic Forms
VerifiedAdded on 2019/10/30
|9
|419
|178
Homework Assignment
AI Summary
This assignment delves into key concepts of linear algebra, providing detailed solutions to problems involving orthogonal matrices, eigenvalues, and quadratic forms. Part 1 focuses on the properties of orthogonal matrices, including their relationship to identity matrices and eigenvalues. It also covers the diagonalization of quadratic forms and the determination of the ellipsoid's equation. Part 2 explores inner products, vector lengths, and angles, along with the Gram-Schmidt process for QR decomposition. Furthermore, it addresses orthogonal bases and the orthogonal projection of a vector onto a plane. The solutions demonstrate the application of these concepts through calculations and explanations, offering a comprehensive understanding of the topics.

Part 1
Question one
Orthogonal matrix
For a matrix to be orthogonal; Transpose¿ inverse
The conditions are
a∧bshould each be equal to 0.5 so that a+ b=1=b+ a and a−b=b−a=0 this makes the
matrix an identity which is orthogonal.
If it is an identity matrix it will as well be a diagonal matrix which is also an orthogonal
matrix.
The matrix will only be orthogonal if a and b have real values.
Question two
If A is symmetric orthogonal then ± 1 are the only possible eigen values
Consider | Av|=¿ v∨¿ for any v ,suppose a is orthogonal and v ≠ 0is an eigenvector having
eigen value λ
av =λv implying |v|=|av|=| λ|∨v∨¿ hence |λ|=1
Which gives the value of λ as either 1∨−1
Question three
The quadratic form 2 x2 +5 y2 +5 z2 + 4 xy−4 xz−8 yz has an associated matrix that can be
orthogonally diagonalized
[
2 2 −2
2 5 −4
−2 −4 5
¿
−λ3+12 λ2−21 λ+10
λ1=1 hence v1=(−2 1 0)
λ2=1 hence v2=(2 0 1)
λ3=10 hence v3=(−1−2 2)
being that λ1=λ2 , v1 is perpendicular ¿ v3∧v2 ¿ v3∧v1 ¿ v2 this can be solved in a linear
combination of
e1= 1
√ 5 ( 2
0
1) ∧e3= 1
3∗(
−1
−2
2
)
Question one
Orthogonal matrix
For a matrix to be orthogonal; Transpose¿ inverse
The conditions are
a∧bshould each be equal to 0.5 so that a+ b=1=b+ a and a−b=b−a=0 this makes the
matrix an identity which is orthogonal.
If it is an identity matrix it will as well be a diagonal matrix which is also an orthogonal
matrix.
The matrix will only be orthogonal if a and b have real values.
Question two
If A is symmetric orthogonal then ± 1 are the only possible eigen values
Consider | Av|=¿ v∨¿ for any v ,suppose a is orthogonal and v ≠ 0is an eigenvector having
eigen value λ
av =λv implying |v|=|av|=| λ|∨v∨¿ hence |λ|=1
Which gives the value of λ as either 1∨−1
Question three
The quadratic form 2 x2 +5 y2 +5 z2 + 4 xy−4 xz−8 yz has an associated matrix that can be
orthogonally diagonalized
[
2 2 −2
2 5 −4
−2 −4 5
¿
−λ3+12 λ2−21 λ+10
λ1=1 hence v1=(−2 1 0)
λ2=1 hence v2=(2 0 1)
λ3=10 hence v3=(−1−2 2)
being that λ1=λ2 , v1 is perpendicular ¿ v3∧v2 ¿ v3∧v1 ¿ v2 this can be solved in a linear
combination of
e1= 1
√ 5 ( 2
0
1) ∧e3= 1
3∗(
−1
−2
2
)
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

So e2=e3∗e1=[
−2
3 √5
√5
3
4
3 √5
]
Then [ x'
y'
z' ]=
( 2
√5
−2
3 √5
−1
3
0 √5
3
−2
3
1
√5
4
3 √5
3
3
)−1
( x
y
z )=
( 2
√5 0 1
√5
−2
3 √5
√5
3
4
3 √5
−1
3
−2
3
2
3
) ( x
y
z )
( 2
√5
−2
3 √ 5
−1
3
0 √5
3
−2
3
1
√5
4
3 √ 5
2
3
) ( 2 2 −2
2 5 −4
−2 −4 5 ) ( 2
√5 0 1
√5
−2
3 √5
√ 5
3
4
3 √5
−1
3
−2
3
2
3
)=
(1 0 0
0 1 0
0 0 10 )
Now expressing q in terms of the new variables gives
Q=xr 2 + yr 2+10 zr 2
Question four
To show that a quadratic equation represent ellipsoid
4
3 x2+ 4
3 y2 + 4
3 z2+ 4
3 xy + 4
3 xz + 4
3 yz=1
The general form of an ellipsoid is
A x2+ B x2+c z2 + Dyz+ Ezx + Fxy+ Hy +Jz + k=0
The matrix
M =
[ A F
2
D
2
F
2 B D
2
E
2
D
2 C ] should be positive definite i.e.
−2
3 √5
√5
3
4
3 √5
]
Then [ x'
y'
z' ]=
( 2
√5
−2
3 √5
−1
3
0 √5
3
−2
3
1
√5
4
3 √5
3
3
)−1
( x
y
z )=
( 2
√5 0 1
√5
−2
3 √5
√5
3
4
3 √5
−1
3
−2
3
2
3
) ( x
y
z )
( 2
√5
−2
3 √ 5
−1
3
0 √5
3
−2
3
1
√5
4
3 √ 5
2
3
) ( 2 2 −2
2 5 −4
−2 −4 5 ) ( 2
√5 0 1
√5
−2
3 √5
√ 5
3
4
3 √5
−1
3
−2
3
2
3
)=
(1 0 0
0 1 0
0 0 10 )
Now expressing q in terms of the new variables gives
Q=xr 2 + yr 2+10 zr 2
Question four
To show that a quadratic equation represent ellipsoid
4
3 x2+ 4
3 y2 + 4
3 z2+ 4
3 xy + 4
3 xz + 4
3 yz=1
The general form of an ellipsoid is
A x2+ B x2+c z2 + Dyz+ Ezx + Fxy+ Hy +Jz + k=0
The matrix
M =
[ A F
2
D
2
F
2 B D
2
E
2
D
2 C ] should be positive definite i.e.

A>0 , AB > F2
4 ∧det ( M ) =0
Now proving our equation
M =
[ 4
3
4
6
4
6
4
6
4
3
4
6
4
6
4
6
4
3 ]Now A= 4
3 >0
AB=( 4
3 )
2
=16
9
While F2
4 = 4
9 = 4
9
Hence AB> F2
4
The det ( M )= 4
3∗
| 4
6
4
6
4
6
4
3 |− 4
6 |4
6
4
6
4
6
4
3 |+ 4
6 ∗
|4
6
4
3
4
6
4
6 |
This gives
16
27 − 8
27 − 8
27 =0
position and length of principal axis
getting matrix
M =
[ 4
3
4
3
4
3
4
3
4
3
4
3
4
3
4
3
4
3
]Now we obtain the eigen values
4 ∧det ( M ) =0
Now proving our equation
M =
[ 4
3
4
6
4
6
4
6
4
3
4
6
4
6
4
6
4
3 ]Now A= 4
3 >0
AB=( 4
3 )
2
=16
9
While F2
4 = 4
9 = 4
9
Hence AB> F2
4
The det ( M )= 4
3∗
| 4
6
4
6
4
6
4
3 |− 4
6 |4
6
4
6
4
6
4
3 |+ 4
6 ∗
|4
6
4
3
4
6
4
6 |
This gives
16
27 − 8
27 − 8
27 =0
position and length of principal axis
getting matrix
M =
[ 4
3
4
3
4
3
4
3
4
3
4
3
4
3
4
3
4
3
]Now we obtain the eigen values
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

[ 4
3 − λ 4
3
4
3
4
3
4
3 −λ 4
3
4
3
4
3
4
3 −λ ]
( 4
3 −λ ) [ 4
3 − λ 4
3
4
3
4
3 −λ ] − 4
3 [ 4
3
4
3
4
3
4
3 − λ ] + 4
3 [ 4
3
4
3 − λ
4
3
4
3 ]
Which gives the equation
λ3+ 4
3 λ2−4 λ
From the equation, we get the eigen values as
λ1=4 , λ2=0 ,∧λ3=0
And the corresponding eigen vectors as
v1 =(1 , 1, 1)
v2=(−1 , 0 , 1)
v3 =(−1 , 1 ,0)
We then normalize the eigen vectors to obtain a matrix
[ 1
√ 3
−1
√2
−1
√2
1
√ 3 0 1
√2
1
√ 3
1
√2 0 ]
We get D= [4 0 0
0 0 0
0 0 0 ]
And the equations
y1= 1
√3 x + 1
√3 y+ 1
√3 z
y2=−1
√ 2 x + 1
√ 2 z
y3=−1
√ 2 x + 1
√2 y
3 − λ 4
3
4
3
4
3
4
3 −λ 4
3
4
3
4
3
4
3 −λ ]
( 4
3 −λ ) [ 4
3 − λ 4
3
4
3
4
3 −λ ] − 4
3 [ 4
3
4
3
4
3
4
3 − λ ] + 4
3 [ 4
3
4
3 − λ
4
3
4
3 ]
Which gives the equation
λ3+ 4
3 λ2−4 λ
From the equation, we get the eigen values as
λ1=4 , λ2=0 ,∧λ3=0
And the corresponding eigen vectors as
v1 =(1 , 1, 1)
v2=(−1 , 0 , 1)
v3 =(−1 , 1 ,0)
We then normalize the eigen vectors to obtain a matrix
[ 1
√ 3
−1
√2
−1
√2
1
√ 3 0 1
√2
1
√ 3
1
√2 0 ]
We get D= [4 0 0
0 0 0
0 0 0 ]
And the equations
y1= 1
√3 x + 1
√3 y+ 1
√3 z
y2=−1
√ 2 x + 1
√ 2 z
y3=−1
√ 2 x + 1
√2 y
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Now the principal axis have the equation
y1= 1
√3 x + 1
√3 y+ 1
√3 z
And length
|| y1||= √((¿ 1
√3 )
2
+( 1
√3 )
2
+( 1
√3 )
2
) ¿
Then || y1||=1
Part 2
Question 1
Inner product is defined in the form of suppose u and v are vectors then
u . v=u1 v1+u2 v2 +… . un vn
In B ( u , v ) = ( u1 , u2 ,u3 ) [ 1 1 1
1 2 0
1 0 3 ] ( v1
v2
v3 )
In the multiplication of a matrix
We have u1∗1+u2∗1+u3∗1, u1∗1+u2∗2+u3 +0 , u1∗1+u2∗0+u3∗3
This is a form of an inner product as it takes on the form given above and gives the eventual
answer as a scalar.
Length of a vector
a=(1 , 1 , 0)
||a||= √a . a= √12 +12+ 02= √2
For b=(0 ,1 , 1)
||b||= √b .b= √2
Finding the angle between the vectors
cosθ= a .b
||a||∗||b|| , where a . b=inner product
Hence obtaining the angle with respect to the inner product gives
a . b=¿cosθ∗¿|a|∨¿|b|∨¿ where θ is theangle between the vectors
But a . b=0+1+0=1
y1= 1
√3 x + 1
√3 y+ 1
√3 z
And length
|| y1||= √((¿ 1
√3 )
2
+( 1
√3 )
2
+( 1
√3 )
2
) ¿
Then || y1||=1
Part 2
Question 1
Inner product is defined in the form of suppose u and v are vectors then
u . v=u1 v1+u2 v2 +… . un vn
In B ( u , v ) = ( u1 , u2 ,u3 ) [ 1 1 1
1 2 0
1 0 3 ] ( v1
v2
v3 )
In the multiplication of a matrix
We have u1∗1+u2∗1+u3∗1, u1∗1+u2∗2+u3 +0 , u1∗1+u2∗0+u3∗3
This is a form of an inner product as it takes on the form given above and gives the eventual
answer as a scalar.
Length of a vector
a=(1 , 1 , 0)
||a||= √a . a= √12 +12+ 02= √2
For b=(0 ,1 , 1)
||b||= √b .b= √2
Finding the angle between the vectors
cosθ= a .b
||a||∗||b|| , where a . b=inner product
Hence obtaining the angle with respect to the inner product gives
a . b=¿cosθ∗¿|a|∨¿|b|∨¿ where θ is theangle between the vectors
But a . b=0+1+0=1

Hence cosθ= 1
√2∗√ 2 =1
2 which means θ=600
Question 2
Using the QR decomposition where R=B=upper triangular ¿ Q= A=orthogonal ¿
AB= [1 1 1
1 3 9
1 9 81 ]
a1= ( 1,1,1 )T , a2= ( 1,3,9 )T ,a3= ( 1,9,81 )T
The vectors of a are column vectors
Now conducting the Gram-Schmidt procedure we have
u1=a1=(1,1,1)
e1= u1
||u1||= 1
√3∗( 1,1,1 )=( 1
√3 , 1
√3 , 1
√3 )
u2=a2− ( a2 . e1 ) e1
¿ ( 1,3,9 )− 13
√3 ( 1
√3 , 1
√3 , 1
√3 )=(−10
3 ,− 4
3 , 11
3 )
e2= u2
||u2||= 3
√237∗(−10
3 ,− 4
3 , 11
3 )=( −10
√237 , −4
√237 , 11
√237 )
u3=a3− ( a3 . e1 ) e1− ( a3 . e2 ) e2
( 1 , 9 ,81 )− 91
√3 ( 1
√ 3 , 1
√3 , 1
√3 )− 845
√237 ( −10
√237 , −4
√237 , 11
√237 )=( 1498
237 ,− 1676
237 , 2713
237 )
e3= u3
||u3||= 237
2713 u3
¿ 237
2713∗( 1498
237 ,− 1676
237 , 2713
237 )=( √ 3
10 ,− √ 39
100 , 1)
Q= [ e1 , e2 , e3 ]=
[ 1
√3
−10
√237 √ 3
10
1
√3
−4
√237 √ 39
100
1
√3
11
√237 1 ]
√2∗√ 2 =1
2 which means θ=600
Question 2
Using the QR decomposition where R=B=upper triangular ¿ Q= A=orthogonal ¿
AB= [1 1 1
1 3 9
1 9 81 ]
a1= ( 1,1,1 )T , a2= ( 1,3,9 )T ,a3= ( 1,9,81 )T
The vectors of a are column vectors
Now conducting the Gram-Schmidt procedure we have
u1=a1=(1,1,1)
e1= u1
||u1||= 1
√3∗( 1,1,1 )=( 1
√3 , 1
√3 , 1
√3 )
u2=a2− ( a2 . e1 ) e1
¿ ( 1,3,9 )− 13
√3 ( 1
√3 , 1
√3 , 1
√3 )=(−10
3 ,− 4
3 , 11
3 )
e2= u2
||u2||= 3
√237∗(−10
3 ,− 4
3 , 11
3 )=( −10
√237 , −4
√237 , 11
√237 )
u3=a3− ( a3 . e1 ) e1− ( a3 . e2 ) e2
( 1 , 9 ,81 )− 91
√3 ( 1
√ 3 , 1
√3 , 1
√3 )− 845
√237 ( −10
√237 , −4
√237 , 11
√237 )=( 1498
237 ,− 1676
237 , 2713
237 )
e3= u3
||u3||= 237
2713 u3
¿ 237
2713∗( 1498
237 ,− 1676
237 , 2713
237 )=( √ 3
10 ,− √ 39
100 , 1)
Q= [ e1 , e2 , e3 ]=
[ 1
√3
−10
√237 √ 3
10
1
√3
−4
√237 √ 39
100
1
√3
11
√237 1 ]
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
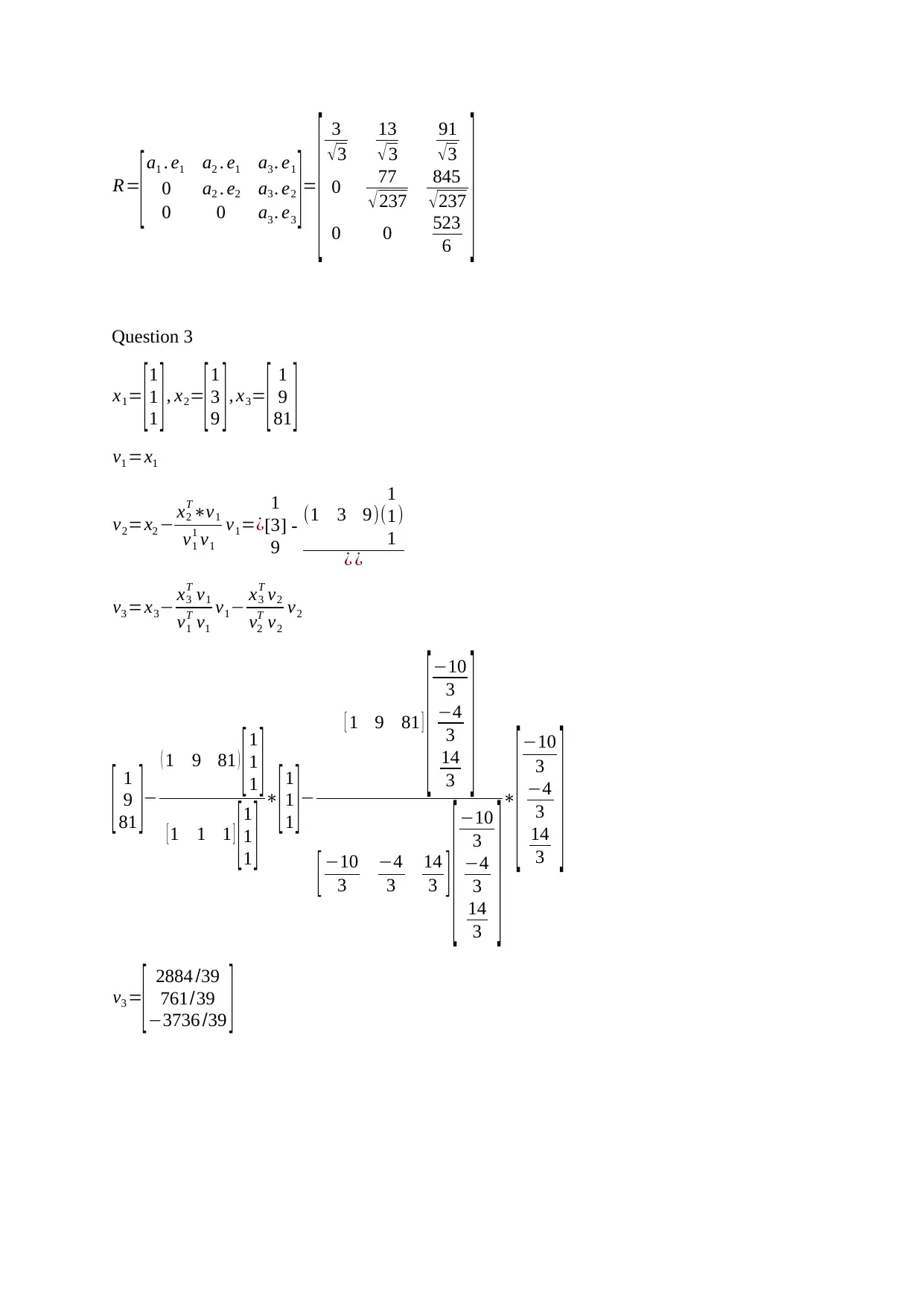
R=
[a1 . e1 a2 . e1 a3 . e1
0 a2 . e2 a3 . e2
0 0 a3 . e3 ]=
[ 3
√3
13
√3
91
√3
0 77
√237
845
√237
0 0 523
6
]
Question 3
x1= [1
1
1 ], x2=
[1
3
9 ], x3= [ 1
9
81 ]
v1 =x1
v2=x2 − x2
T∗v1
v1
1 v1
v1=¿[
1
3
9
] - (1 3 9)(
1
1
1
)
¿ ¿
v3 =x3− x3
T v1
v1
T v1
v1− x3
T v2
v2
T v2
v2
[ 1
9
81 ]−
( 1 9 81 ) [ 1
1
1 ]
[ 1 1 1 ] [ 1
1
1 ] ∗
[ 1
1
1 ]−
[ 1 9 81 ]
[ −10
3
−4
3
14
3
]
[ −10
3
−4
3
14
3 ] [ −10
3
−4
3
14
3
] ∗
[ −10
3
−4
3
14
3
]
v3 =
[ 2884 /39
761/39
−3736 /39 ]
[a1 . e1 a2 . e1 a3 . e1
0 a2 . e2 a3 . e2
0 0 a3 . e3 ]=
[ 3
√3
13
√3
91
√3
0 77
√237
845
√237
0 0 523
6
]
Question 3
x1= [1
1
1 ], x2=
[1
3
9 ], x3= [ 1
9
81 ]
v1 =x1
v2=x2 − x2
T∗v1
v1
1 v1
v1=¿[
1
3
9
] - (1 3 9)(
1
1
1
)
¿ ¿
v3 =x3− x3
T v1
v1
T v1
v1− x3
T v2
v2
T v2
v2
[ 1
9
81 ]−
( 1 9 81 ) [ 1
1
1 ]
[ 1 1 1 ] [ 1
1
1 ] ∗
[ 1
1
1 ]−
[ 1 9 81 ]
[ −10
3
−4
3
14
3
]
[ −10
3
−4
3
14
3 ] [ −10
3
−4
3
14
3
] ∗
[ −10
3
−4
3
14
3
]
v3 =
[ 2884 /39
761/39
−3736 /39 ]
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Orthogonal basis W =span {
[1
1
1 ] [ −10
3
−4
3
14
3 ][ 2884
39
761
39
−3736
39 ]}
othornormal basis R=span { v1
||v1|| , v2
||v2|| , v3
||v3|| }
¿∨v1∨¿= √12+ 12+12 = √3
||v2||= √ (−10
3 )2
+¿ (−4
3 )2
+¿ (14
3 )2
= √ 312
9
¿∨v3∨¿=4720/39
R=span
{[ 1
√3
1
√3
1
√3
] [ − 10
3
√ 312
9
− 4
3
√ 312
9
14
3
√ 312
9
] [ 721
1180
761
4720
3736
4720
] }
¿
[ 1
√3
1
√3
1
√3
] [ −10
√312
−4
√312
14
√312
[ 721
1180
761
4720
3736
4720
] ]
Question 4
a) u=(4 , 2 ,1)
v1 =( 1
3 , 2
3 ,−2
3 )
[1
1
1 ] [ −10
3
−4
3
14
3 ][ 2884
39
761
39
−3736
39 ]}
othornormal basis R=span { v1
||v1|| , v2
||v2|| , v3
||v3|| }
¿∨v1∨¿= √12+ 12+12 = √3
||v2||= √ (−10
3 )2
+¿ (−4
3 )2
+¿ (14
3 )2
= √ 312
9
¿∨v3∨¿=4720/39
R=span
{[ 1
√3
1
√3
1
√3
] [ − 10
3
√ 312
9
− 4
3
√ 312
9
14
3
√ 312
9
] [ 721
1180
761
4720
3736
4720
] }
¿
[ 1
√3
1
√3
1
√3
] [ −10
√312
−4
√312
14
√312
[ 721
1180
761
4720
3736
4720
] ]
Question 4
a) u=(4 , 2 ,1)
v1 =( 1
3 , 2
3 ,−2
3 )

v2=( 2
3 , 1
3 , 2
3 )
The orthogonal projection of u on to the plane spanned by vectors v1 ∧v2
Remark
v1 . v1= ( 1
3 )2
+( 2
3 )2
+ (−2.3 )2=1
v1 . v2= ( 1
3∗2
3 )+ ( 2
3 ∗1
3 )+( −2
3 ∗2
3 )=0
v2 . v2= ( 2
3 )2
+( 1
3 )2
+ ( 2
3 )2
=1
In this case we get that v1 ∧v2 areperpendicular with length √1=1
Therefore, the vectors
u1=1∗v1= ( 1
3 , 2
3 ,−2
3 )∧u2=1∗v2 =( 2
3 , 1
3 , 2
3 ) form the orthogonal basis of the plane.
therefore
u . u1= 4
3 + 4
3 − 2
3 =2
And
u . u2= 8
3 + 2
3 + 2
3 =4
In conclusion, the projection of u can be obtained by the formula
u¿∨¿= ( u . u1 ) u1+¿ ¿(u . u2 ¿ u2
¿ 2∗( 1
3 , 2
3 ,−2
3 )+ 4∗( 2
3 , 1
3 , 2
3 )=( 10
3 , 8
3 , 4
3 )
b) obtain the cross product
v3 =v1∗v2=
[ i j k
1
3
2
3
−2
3
2
3
1
3
2
3 ]= 2
3 i− 2
3 j−1
3 k
Now computing the component orthogonal to the plane is the projection of u onto v3
parallel to the plane
pr ⊥v3
u= ( u .u3 ) u3=1∗u3=( 2
3 ,− 2
3 ,−1
3 )
3 , 1
3 , 2
3 )
The orthogonal projection of u on to the plane spanned by vectors v1 ∧v2
Remark
v1 . v1= ( 1
3 )2
+( 2
3 )2
+ (−2.3 )2=1
v1 . v2= ( 1
3∗2
3 )+ ( 2
3 ∗1
3 )+( −2
3 ∗2
3 )=0
v2 . v2= ( 2
3 )2
+( 1
3 )2
+ ( 2
3 )2
=1
In this case we get that v1 ∧v2 areperpendicular with length √1=1
Therefore, the vectors
u1=1∗v1= ( 1
3 , 2
3 ,−2
3 )∧u2=1∗v2 =( 2
3 , 1
3 , 2
3 ) form the orthogonal basis of the plane.
therefore
u . u1= 4
3 + 4
3 − 2
3 =2
And
u . u2= 8
3 + 2
3 + 2
3 =4
In conclusion, the projection of u can be obtained by the formula
u¿∨¿= ( u . u1 ) u1+¿ ¿(u . u2 ¿ u2
¿ 2∗( 1
3 , 2
3 ,−2
3 )+ 4∗( 2
3 , 1
3 , 2
3 )=( 10
3 , 8
3 , 4
3 )
b) obtain the cross product
v3 =v1∗v2=
[ i j k
1
3
2
3
−2
3
2
3
1
3
2
3 ]= 2
3 i− 2
3 j−1
3 k
Now computing the component orthogonal to the plane is the projection of u onto v3
parallel to the plane
pr ⊥v3
u= ( u .u3 ) u3=1∗u3=( 2
3 ,− 2
3 ,−1
3 )
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 9
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





