MTH-1 Project II: Parametric Equations of Projectile Motion
VerifiedAdded on 2023/01/19
|6
|1183
|91
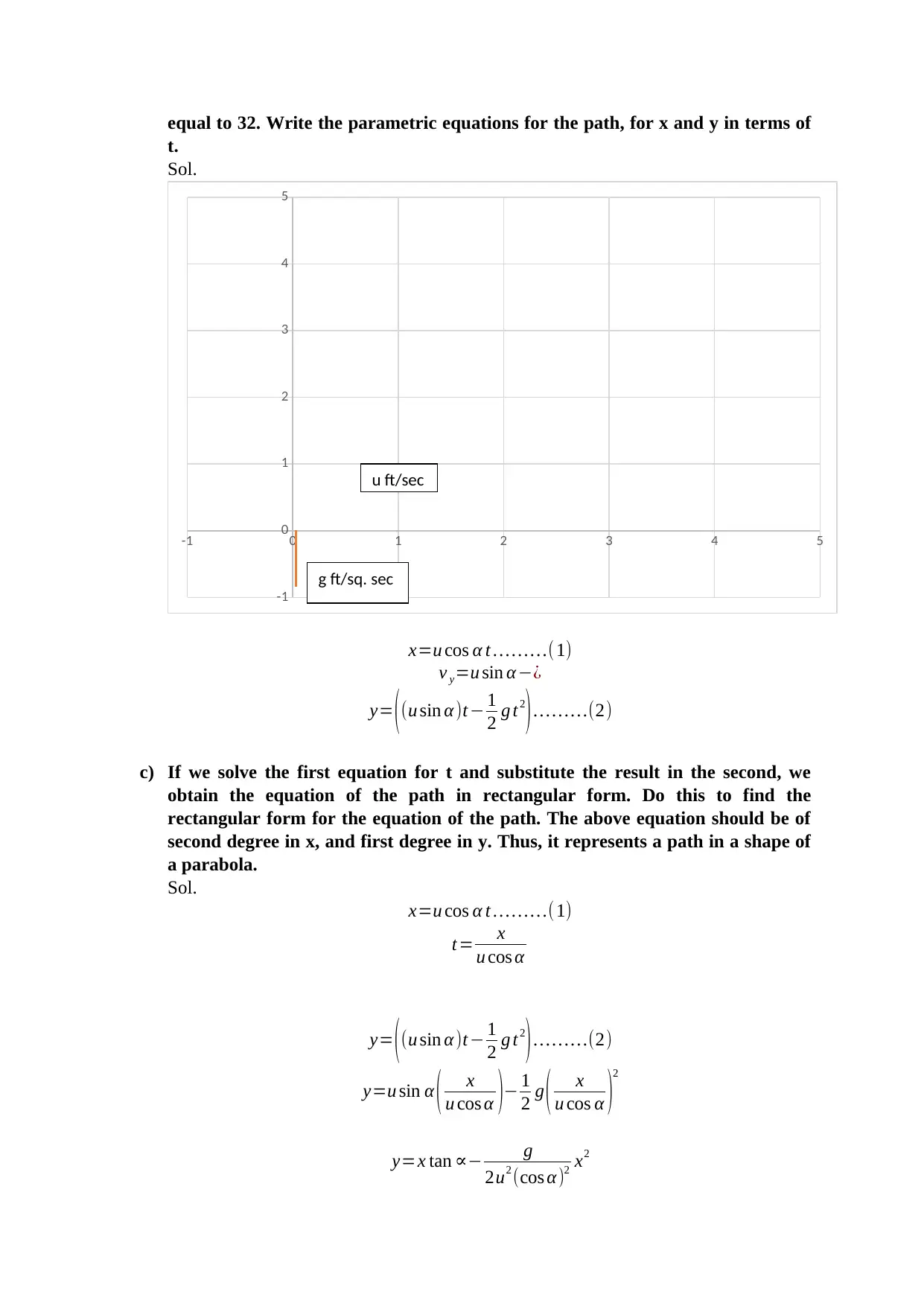
Homework Assignment
AI Summary
This assignment, a solution for an MTH-1 project, delves into the analysis of projectile motion using parametric equations. It begins by establishing the foundational principles of projectile motion, considering factors such as initial velocity and the angle of projection, while neglecting air resistance. The solution then develops parametric equations to describe the horizontal and vertical components of the projectile's path, incorporating the effect of gravity. The assignment proceeds to convert these parametric equations into a rectangular form to derive the equation of the path, demonstrating the parabolic nature of the trajectory. Furthermore, it applies these equations to solve a specific problem, calculating the range (distance traveled) and maximum height attained by a stone thrown at a given velocity and angle. Both parametric and rectangular forms are utilized to solve this problem, providing a comprehensive understanding of projectile motion analysis. The solution also uses the vertex formula of a parabola to determine the maximum height, offering a complete analysis of the projectile's flight.
1 out of 6












![[object Object]](/_next/static/media/star-bottom.7253800d.svg)