Pavilion Design Project: Ellipse and Parabola Geometry Application

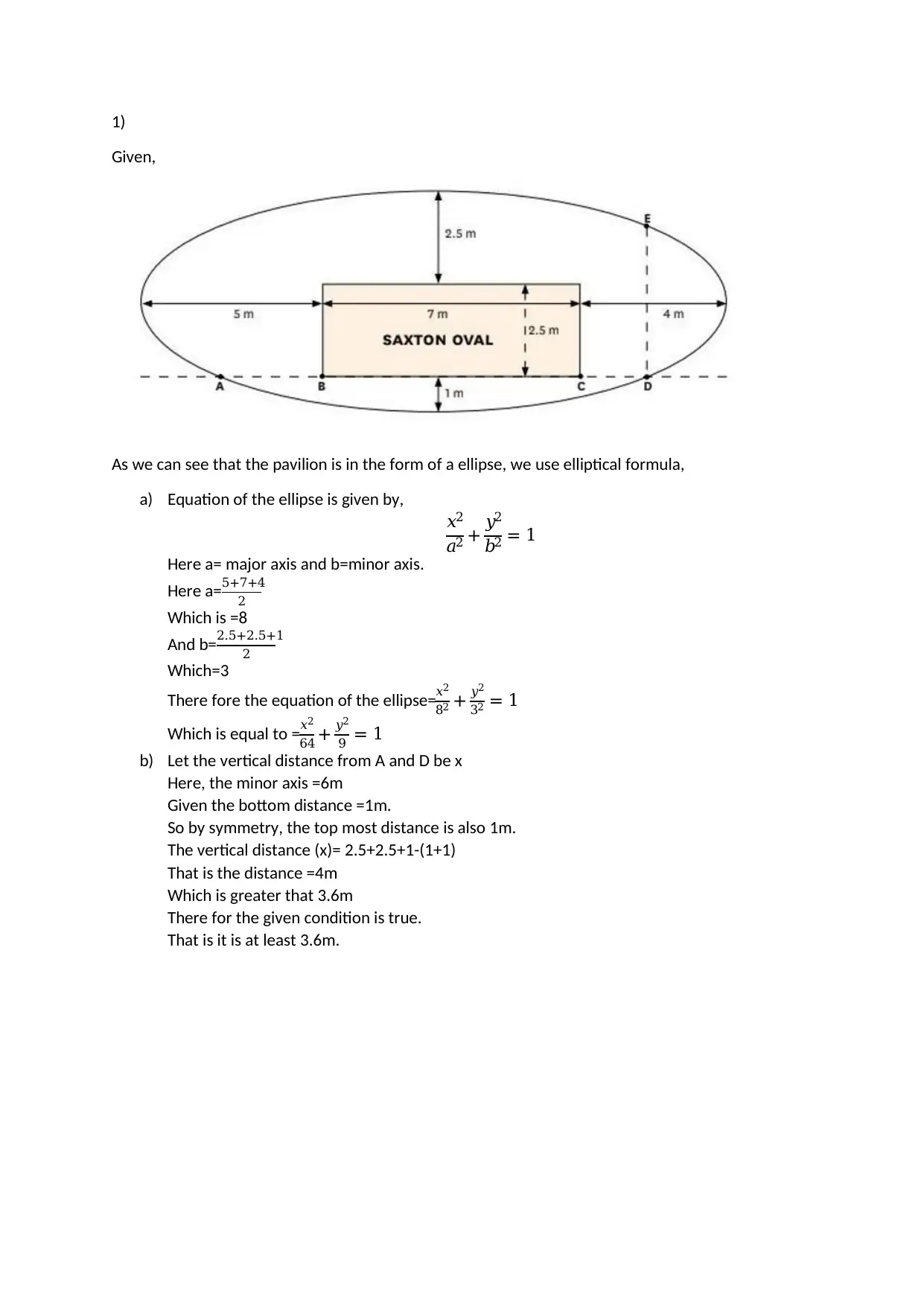
This assignment focuses on applying geometric principles, specifically ellipses and parabolas, to the design of a pavilion. It involves calculating the equation of an ellipse based on given dimensions, determining vertical distances, and comparing them to specified requirements. The assignment also includes finding the equation of a parabola given its maximum height and width, calculating the building's width at a certain height, and comparing an original parabolic model to an adapted model in terms of height, width, and area coverage. The solution provides step-by-step calculations and explanations for each part of the problem. Desklib offers more solved assignments and study tools for students.

1)
Given,
As we can see that the pavilion is in the form of a ellipse, we use elliptical formula,
a) Equation of the ellipse is given by,
𝑥2
𝑎2 + 𝑦2
𝑏2 = 1
Here a= major axis and b=minor axis.
Here a=5+7+4
2
Which is =8
And b=2.5+2.5+1
2
Which=3
There fore the equation of the ellipse=𝑥2
82 + 𝑦2
32 = 1
Which is equal to =𝑥2
64 + 𝑦2
9 = 1
b) Let the vertical distance from A and D be x
Here, the minor axis =6m
Given the bottom distance =1m.
So by symmetry, the top most distance is also 1m.
The vertical distance (x)= 2.5+2.5+1-(1+1)
That is the distance =4m
Which is greater that 3.6m
There for the given condition is true.
That is it is at least 3.6m.

2)
a)
given maximum height=9.5m and width at ground level = 16m
the equation of a parabola is given by,
𝑦2 = −4𝑎𝑥
Here y=9.5,
x=16
plugging into the parabolic equation, we get
9.52 = −4 ∗ 𝑎 ∗ 16
a=−1.410
There fore the general equation of the parabola is,
𝑦2 = −1.410𝑥
b)
width of the building at a height of 3.6m
this is formed by substituting y=3.6 at the parabolic equation.
That is y=3.6 in 𝑦2 =-1.410x
The solution for this equation is x=9.19m

3)
Given, the vertical height of the parabola = 3.6m at the same width as that of ellipse.
y=3.6m, x is to find out.
the equation of a parabola is given by,
𝑦2 = −4𝑎𝑥
Where a=-1.410
Substituting in the parabolic equation,
3.62 = −4 ∗ −1.410 ∗ 𝑥
x=2.297m
plugging into the parabolic equation, we get
𝑦2 = −4𝑎𝑥
3.62 = −4 ∗ −1.410 ∗ 2.297
The difference between original model and adapted model is,
That is the original model has larger height and larger width than the adapted model.
That is area covered is more for original than the adapted model.
The entrance perfectly fits inside the original parabola where as it doesn’t fit in the adapted model.