MEng Numerical Solutions of Partial Differential Equations Assignment

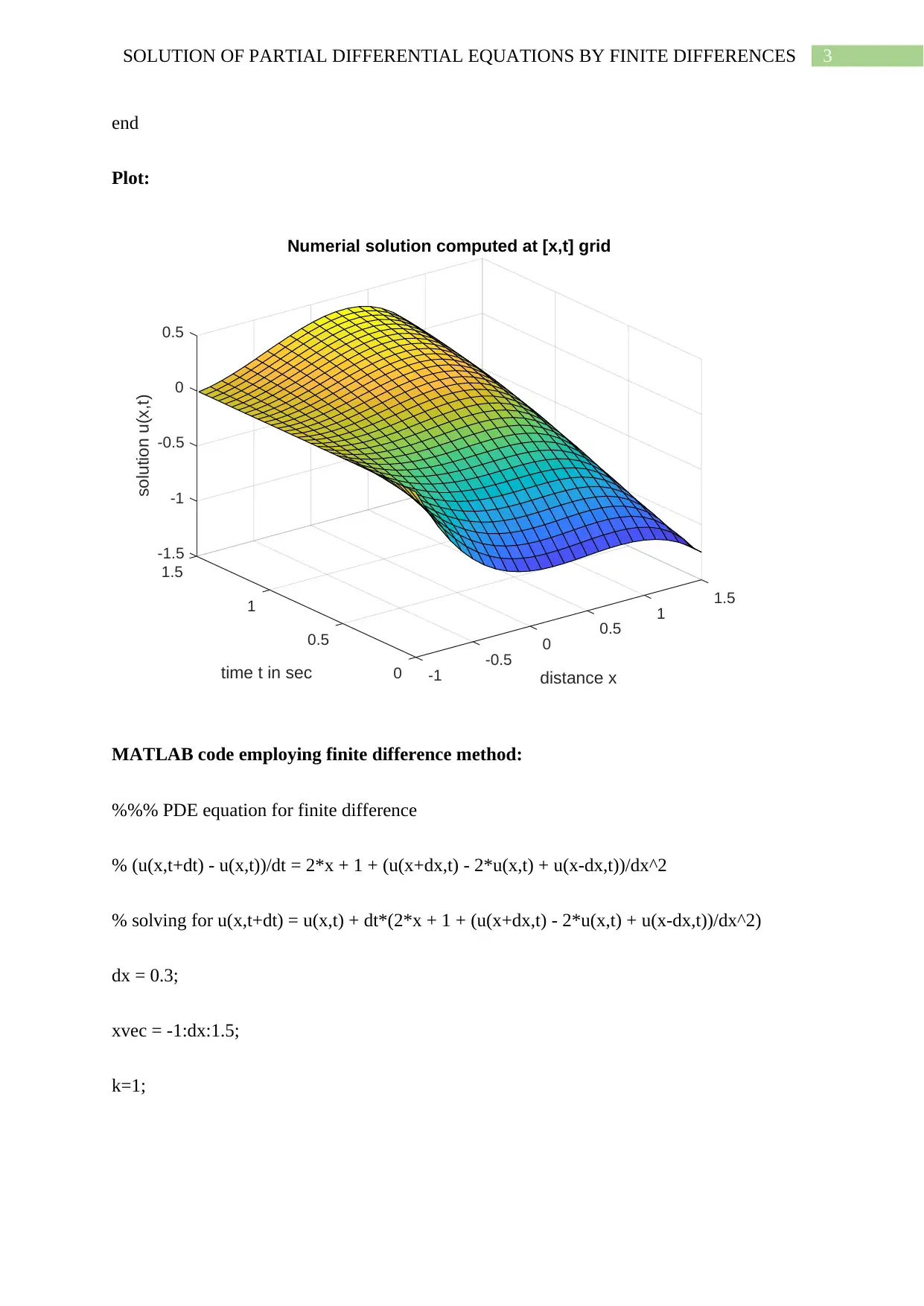
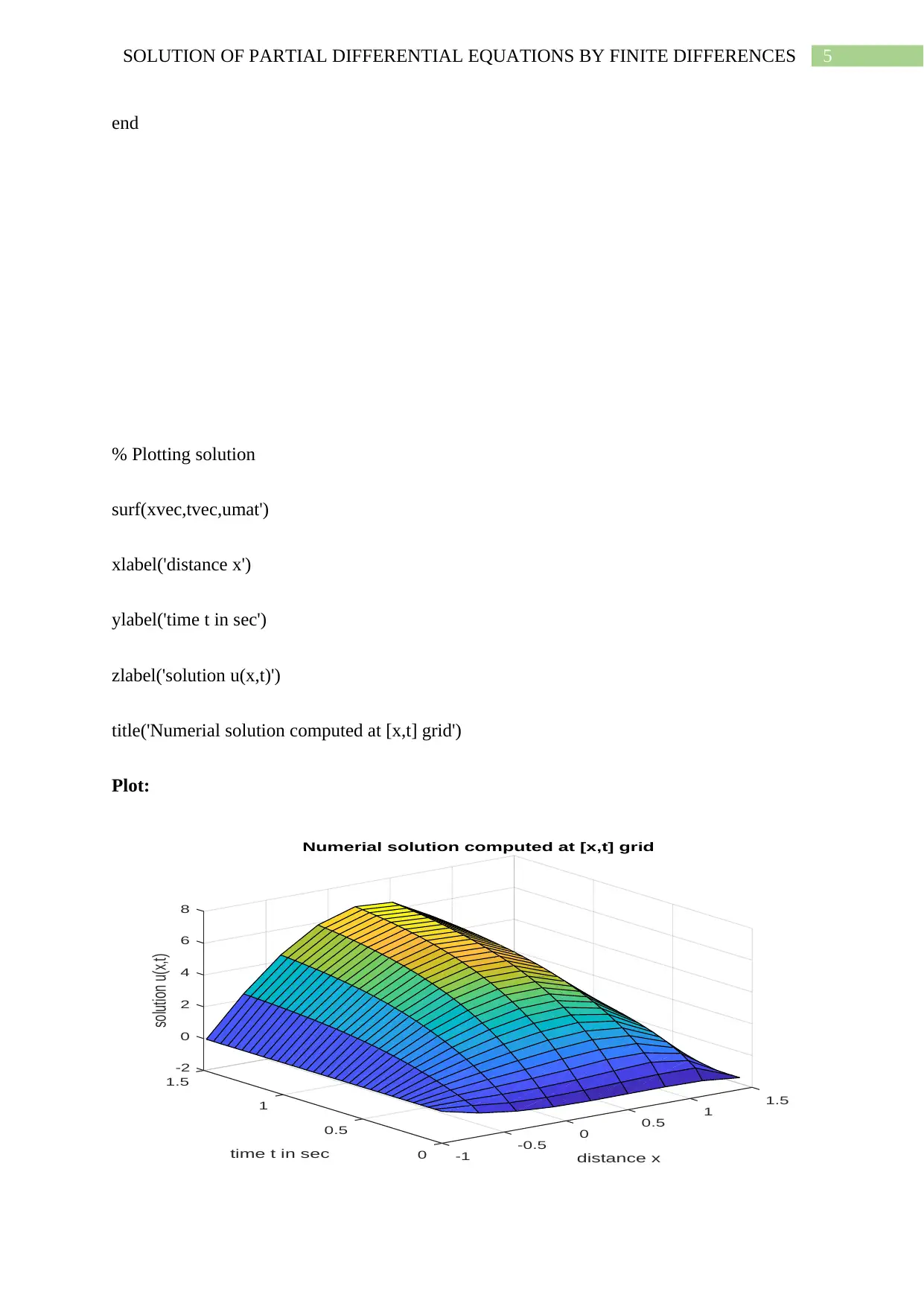
This assignment presents solutions to partial differential equations (PDEs) using the finite difference method implemented in MATLAB. The first part addresses a 1D PDE, providing MATLAB code using both the built-in `pdepe` function and a custom finite difference implementation. It includes initial and boundary conditions, along with plots of the numerical solutions. The second part extends the approach to a 2D heat equation, also solved using the finite difference method in MATLAB. The assignment covers setting up the problem, defining the grid, applying boundary conditions, and iteratively solving for the temperature distribution until a steady state is reached. Contour and pcolor plots are included to visualize the steady-state temperature distribution. The assignment demonstrates the practical application of finite difference methods for solving PDEs and provides detailed MATLAB code and plots for each problem.

Running head: PARTIAL DIFFERENTIAL EQUATIONS
PARTIAL DIFFERENTIAL EQUATIONS
Name of the Student
Name of the University
Author Note

1SOLUTION OF PARTIAL DIFFERENTIAL EQUATIONS BY FINITE DIFFERENCES
3.1:
u
t =2 x +1+❑2 u
x2 , -1<= x <= 1.5
Initial conditions:
u(x,0) = -x^3/3 + x^2/2 –x/6 -1, -1<= x <= 1.5
Boundary conditions:
u(-1,t) = 0, u(1.5,t) = -5/4
c = 1, f = x + u/x, s = 2x
MATLAB code using built-in pdepe function:
xmesh = -1:0.1:1.5;
timespan = 0:0.045:1.5;
sol = pdepe(0,@mypde_description,@mypde_ic,@mypde_bc,xmesh,timespan);
surf(xmesh,timespan,sol)
xlabel('distance x')
ylabel('time t in sec')
zlabel('solution u(x,t)')
title('Numerial solution computed at [x,t] grid')

2SOLUTION OF PARTIAL DIFFERENTIAL EQUATIONS BY FINITE DIFFERENCES
% defining pde function
function [c,f,s] = mypde_description(x,t,u,dudx)
c=1;
f=x+dudx;
s=2*x;
end
% applying initial condition
function u0 = mypde_ic(x)
u0=-x^3/3 + x^2/2 -x/6 - 1;
end
% applying boundary conditions
function [pl,ql,pr,qr] = mypde_bc(xl,ul,xr,ur,t)
pl = ul;
ql=0;
pr = ur+(5/4);
qr=0;

3SOLUTION OF PARTIAL DIFFERENTIAL EQUATIONS BY FINITE DIFFERENCES
end
Plot:
-1.5
1.5
-1
1.5
-0.5
solution u(x,t)
1 1
Numerial solution computed at [x,t] grid
0
time t in sec
0.5
distance x
0.5
0.5 0
-0.5
0 -1
MATLAB code employing finite difference method:
%%% PDE equation for finite difference
% (u(x,t+dt) - u(x,t))/dt = 2*x + 1 + (u(x+dx,t) - 2*u(x,t) + u(x-dx,t))/dx^2
% solving for u(x,t+dt) = u(x,t) + dt*(2*x + 1 + (u(x+dx,t) - 2*u(x,t) + u(x-dx,t))/dx^2)
dx = 0.3;
xvec = -1:dx:1.5;
k=1;

4SOLUTION OF PARTIAL DIFFERENTIAL EQUATIONS BY FINITE DIFFERENCES
dt = (dx^2)/(2*k); % employing stability criterion. dt <= dx^2/2k, where k is any positive
integer. k ~= 0.
tvec = 0:dt:1.5;
umat = zeros(length(xvec),length(tvec)); % initializing u(x,t) with zeros
% initial condition u(x,0) = -x^3/3 + x^2/2 - x/6 - 1 when -1<=x<=1.5
umat(:,1) = -(xvec.^3)./3 + (xvec.^2)./2 - xvec./6 - 1;
% Boundary Conditions
umat(1,:) = 0; % u(-1,t) = 0
umat(end,:) = -5/4; % u(1.5,t) = -5/4
% Employing finite difference formula
for tcount=1:length(tvec)-1
for xcount = 2:length(xvec) - 1
umat(xcount,tcount + 1) = umat(xcount,tcount) + k*dt*(2*xcount + 1 +
(umat(xcount+1,tcount) - 2*umat(xcount,tcount) + umat(xcount-1,tcount))/dx^2);
end

5SOLUTION OF PARTIAL DIFFERENTIAL EQUATIONS BY FINITE DIFFERENCES
end
% Plotting solution
surf(xvec,tvec,umat')
xlabel('distance x')
ylabel('time t in sec')
zlabel('solution u(x,t)')
title('Numerial solution computed at [x,t] grid')
Plot:
-2
1.5
0
2
1.5
solution u(x,t)
1
4
1
Numerial solution computed at [x,t] grid
time t in sec
6
0.5
distance x
8
0.5 0
-0.5
0 -1

6SOLUTION OF PARTIAL DIFFERENTIAL EQUATIONS BY FINITE DIFFERENCES
Hence, the finite difference method approximately solves the partial differential equation,
however the u values are slightly larger than the values of obtained by employing pdepe
method.
Problem 3.2:
In this case the partial differential equation of 2-dimensional heat equation is taken of the
form of problem 3.3.3 which is given below.
∂u
∂ t = k
ρ Cp ( ∂2 u
∂ x2 + ∂2 u
∂ y2 ) + Q
ρCp
Here, let ρ = 1, Cp = 1, Q = yx, k = 1 are assumed as parameters for the above heat equation.
MATLAB code:
% specifying heat equation for finite difference
% (T(x,t+dt) - T(x,t))/dt = Q/(p*Cp) + (k/p*Cp)*(((T(x+dx,t) - 2*T(x,t) + T(x-dx,t))/dx^2 +
(T(y+dy,t) - 2*T(y,t) + T(y-dy,t))/dy^2)))
rho = 1; Cp = 1;
n = 10; %grid has n - 2 interior points per dimension (overlapping)
x = linspace(0,1,n); dx = x(2)-x(1); y = x; dy = dx;
TOL = 1e-6;
T = zeros(n);
% defining boundaries
T(1,1:n) = 10;
T(n,1:n) = 1;

7SOLUTION OF PARTIAL DIFFERENTIAL EQUATIONS BY FINITE DIFFERENCES
T(1:n,1) = 1;
T(1:n,n) = 1;
dt = dx^2/4;
error = 1; k = 0;
while error > TOL
k = k+1;
Told = T;
for i = 2:n-1
for j = 2:n-1
T(i,j) = (1/(rho*Cp))*dt*((Told(i+1,j)-2*Told(i,j)+Told(i-1,j))/dx^2 ...
+ (Told(i,j+1)-2*Told(i,j)+Told(i,j-1))/dy^2 + (i*j)/(rho*Cp)) ...
+ Told(i,j);
end
end
error = max(max(abs(Told-T)));
end
subplot(2,1,1),contour(x,y,T),
title('Steady state temperature')

8SOLUTION OF PARTIAL DIFFERENTIAL EQUATIONS BY FINITE DIFFERENCES
xlabel('x')
ylabel('y')
colorbar
subplot(2,1,2)
pcolor(x,y,T)
shading interp
title('Steady state temperature'),xlabel('x'),ylabel('y'),colorbar
Plot:
Steady state temperature
0 0.2 0.4 0.6 0.8 1
x
0
0.5
1
y
2
4
6
8
10
0 0.2 0.4 0.6 0.8 1
x
0
0.5
1
y
Steady state temperature
2
4
6
8
10

9SOLUTION OF PARTIAL DIFFERENTIAL EQUATIONS BY FINITE DIFFERENCES