Assessment Task 4: Perimeter, Area, Volume, Pythagoras Theorem

This document presents the solutions to Assessment Task 4, focusing on perimeter, area, volume, Pythagoras Theorem, and trigonometric ratios. It includes detailed step-by-step calculations for seven questions, covering various shapes such as rectangles, triangles, and circles, and their respective perimeter and area calculations. The solutions also address volume calculations for square-based pyramids, triangular prisms, cylinders, and cones. Practical problems involving vegetable patch edging costs, soil volume, and surface area calculations are solved. Furthermore, the document demonstrates the application of the Pythagoras Theorem to find missing sides and heights, as well as the use of trigonometric ratios to determine missing angles in triangles. The accuracy of the solutions is verified using geometric properties. This comprehensive assignment provides a clear understanding of the concepts and their applications.

TABLE OF CONTENTS
Table of Contents.............................................................................................................................1
ASSESSMENT TASK 4.................................................................................................................2
Question 1........................................................................................................................................2
A..................................................................................................................................................2
B...................................................................................................................................................2
Question 2........................................................................................................................................3
Question 3........................................................................................................................................4
A. Perimeter of patch...................................................................................................................4
B. Perimeter of patch...................................................................................................................4
C. Cost of edging.........................................................................................................................5
D. Volume of soil........................................................................................................................5
E. Surface area.............................................................................................................................5
F. Composite soil required...........................................................................................................5
Question 4........................................................................................................................................6
Question 5........................................................................................................................................8
Question 6........................................................................................................................................8
(i) Missing side............................................................................................................................9
(ii) Missing angle.........................................................................................................................9
(iii) Checking answer.................................................................................................................10
Question 7......................................................................................................................................10
1

ASSESSMENT TASK 4
Question 1
A
x = 3 meter and y = 5 meter as opposite sides of rectangle are equal
X= 5 cm
y can be calculated using pythagorus theorem
y2 = 52 – 2.52
y2 = 25 – 6.25
y = 4.33 cm
B.
Radius of circle is half of the diameter. Given that diameter is 2.75 cm, radius is equals to 1.375
2

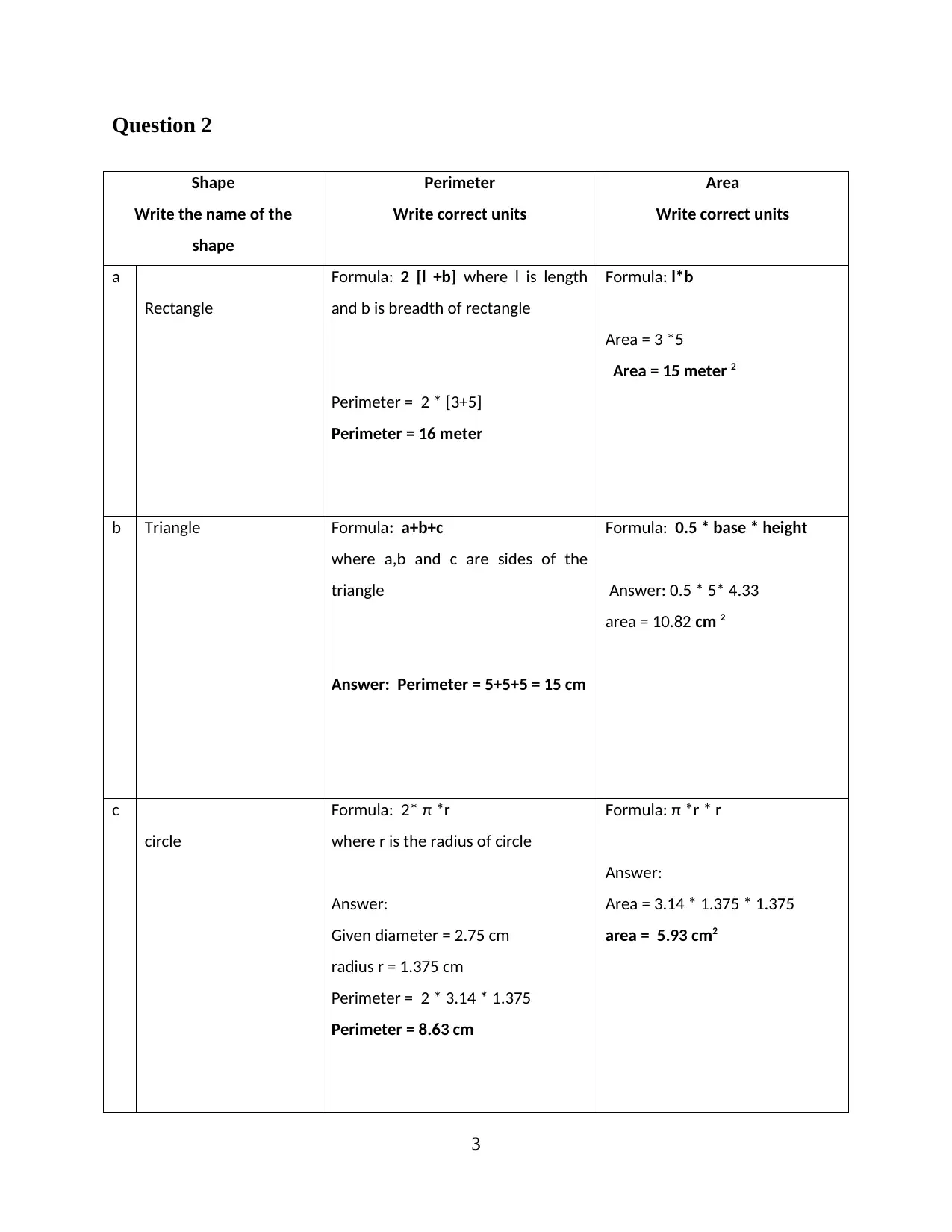
Question 2
Shape
Write the name of the
shape
Perimeter
Write correct units
Area
Write correct units
a
Rectangle
Formula: 2 [l +b] where l is length
and b is breadth of rectangle
Perimeter = 2 * [3+5]
Perimeter = 16 meter
Formula: l*b
Area = 3 *5
Area = 15 meter 2
b Triangle Formula: a+b+c
where a,b and c are sides of the
triangle
Answer: Perimeter = 5+5+5 = 15 cm
Formula: 0.5 * base * height
Answer: 0.5 * 5* 4.33
area = 10.82 cm 2
c
circle
Formula: 2* π *r
where r is the radius of circle
Answer:
Given diameter = 2.75 cm
radius r = 1.375 cm
Perimeter = 2 * 3.14 * 1.375
Perimeter = 8.63 cm
Formula: π *r * r
Answer:
Area = 3.14 * 1.375 * 1.375
area = 5.93 cm2
3

Question 3
A. Perimeter of patch
The vegetable patch will be in shape of rectangle with length 6 meter and width 2 meter.
Perimeter of rectangle = 2 [Length + width]
= 2 * [2+6]
Perimeter = 16 meter
B. Perimeter of patch
New length of rectangular part = 4 meter
Diameter of semicircle = 2 meter
Radius of semicircle = 1 meter
The two semicircles each of diameter 2 meter makes one circle. Thus circumference of circle is
= 2 * 3.14 * r
4

Perimeter of circle = 2 * 3.14 * 1 = 6.28 meter
Total perimeter of new patch = Perimeter of circle + perimeter of two sides of rectangle
= 6.28 + 4 + 4
Perimeter = 14.28 meter
C. Cost of edging
Unit cost of edging = $3.97 per meter
Perimeter of vegetable patch = 14.28 meter
Thus edging will be purchased for 15 meter.
Cost of edging vegetable patch = 3.97 * 15 = $ 59.55
D. Volume of soil
Depth = 200 mm = 0.2 meter
Given length and width of rectangle are 6 and 2 meter respectively
Volume of rectangle = length * width * depth
Volume = 6 * 2 * 0.2
Volume = 2.4 meter 3
Volume of semi-circle = 0.5 * π r2h
Radius of semi-circle = 1 meter
Volume of semi-circle = 0.5 * 3.14 * 1 *1 * 0.2 = 0.314
As there are two semi-circles so volume of both = 2 * 0.314 = 0.628 meter 3
Total volume = 2.4 + 0.628 = 3.02 meter 3
Volume of soil needed to remove = 3.02 meter 3
E. Surface area
Surface area for rectangular part- A=2 (wl+ hl+ hw)
= 2*(2*4+0.2*4+0.2*2)
= 18.4 m2
Surface area for circular part-
A=2πrh+2πr2
5

=2π * 1 * 0.2+ 2π * 12
=7.53982 m2
Total Surface area= 18.4 + 7.53982 = 25.93982 m2
F. Composite soil required
Volume to be filled = 3.02 meter 3
Ratio of composite and excavated soil = 3:1
Thus volume of composite soil which will be needed = [3.02 * 3] /4 = 2.26 meter 3
Question 4
Shape Name Volume (units)
a
Square based
pyramid Area of the base= 7 cm x 7 cm =
49 cm2
= 49 cm2 x 15 cm x 1/3
= 735 cm3 x 1/3
= 245 cm3
b Triangular
prism
Volume = area of base * length of
prism
Prism length = 12 cm
Area of base triangle = 0.5 * base *
height
Base = 4 cm and height = 6 cm
Area = 0.5 * 4 * 6 = 12 cm2
Volume of triangular prism = 12 *
12 = 144 cm3
6

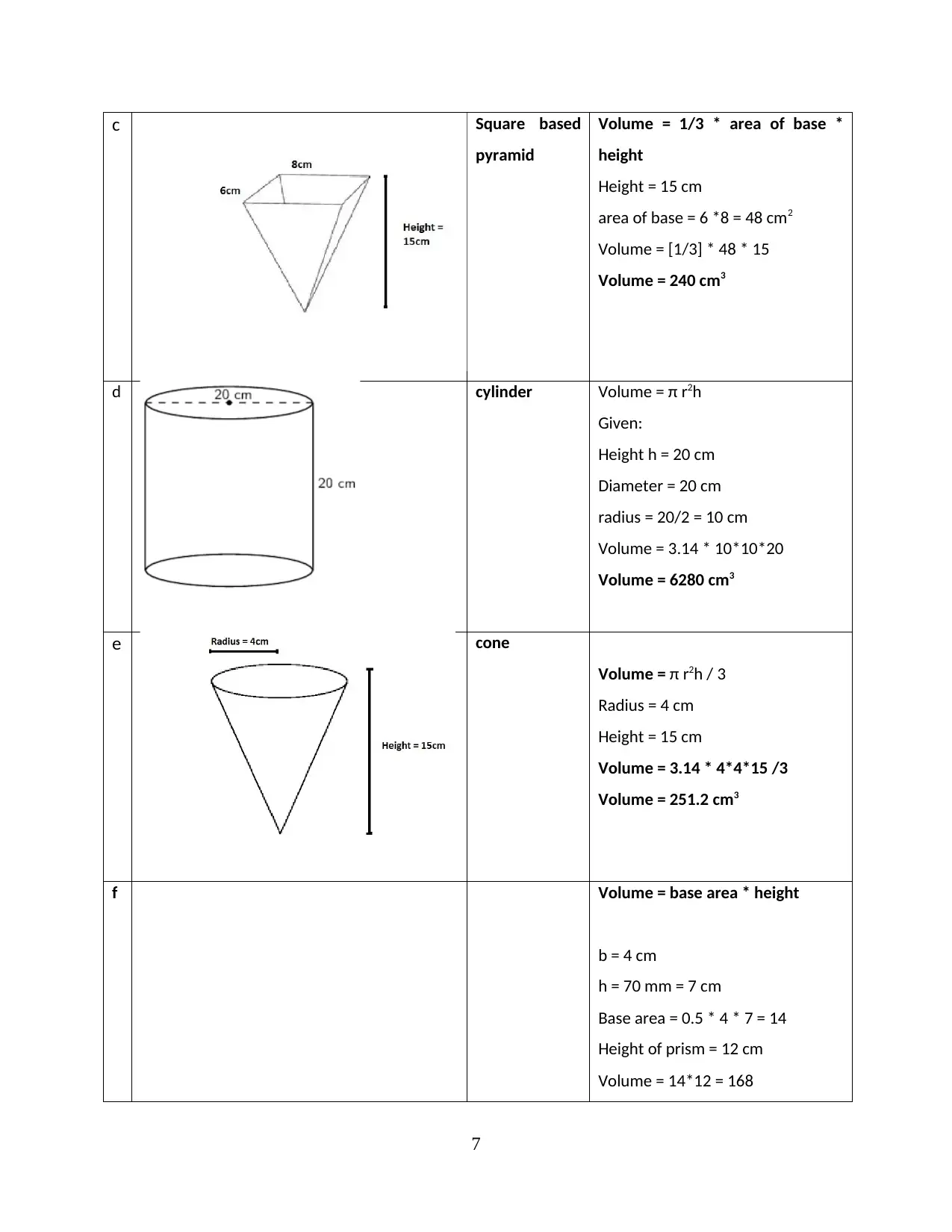
c Square based
pyramid
Volume = 1/3 * area of base *
height
Height = 15 cm
area of base = 6 *8 = 48 cm2
Volume = [1/3] * 48 * 15
Volume = 240 cm3
d cylinder Volume = π r2h
Given:
Height h = 20 cm
Diameter = 20 cm
radius = 20/2 = 10 cm
Volume = 3.14 * 10*10*20
Volume = 6280 cm3
e cone
Volume = π r2h / 3
Radius = 4 cm
Height = 15 cm
Volume = 3.14 * 4*4*15 /3
Volume = 251.2 cm3
f Volume = base area * height
b = 4 cm
h = 70 mm = 7 cm
Base area = 0.5 * 4 * 7 = 14
Height of prism = 12 cm
Volume = 14*12 = 168
7

b = 4cm
h = 70 mm
H = 12 cm
Triangular
prism
Volume = 168 cm3
Question 5
Height of the tree = AB
Length of ladder AC = 9 meter
Distance between base of trunk and ladder = BC = 4 meter
The arrangement forms a right angle triangle
Using Pythagoras theorem:
AC2 = AB2 + BC2
AB2 = AC2 - BC2
8

AB2 = 92 - 42
AB2 = 81 – 16
AB2 = 65
AB = 8.06 meter
Thus cat is at height of 8.06 meter
Question 6
(i) Missing side
Using the law of sines:
8 /sin 25 = x/sin 90
Sin 90 = 1
8 /sin 25 = x
x = 18.95 cm
Using Pythagoras theorem:
x2 = y2 + 82
y2 = (18.95)2 -64
y2 = (18.95)2 -64
y2 = 295.1
y = 17.17 cm
(ii) Missing angle
As per trigonometric ratio; in right angle triangle cos x = base / height
9

From figure it can be seen that:
Cos a = 8 / 18.95
Cos a = 0.422
Angle a = 65.04°
Approximately angle = 65 degree
(iii) Checking answer
The answer can be verified by using the property that sum of angles of a triangle is 180.
Thus for given question all three angles are 90, 25 and 65 which sum up to 180 degrees. It proves
that answer is correct.
Question 7
Using Law of Sines,
So,
10

= B =
B= 42°
Find missing angle 2
C= 180- A+B = 180 – 76 + 42
C= 62°
11