University Physics: Heat Diffusion Equation and MATLAB Simulation

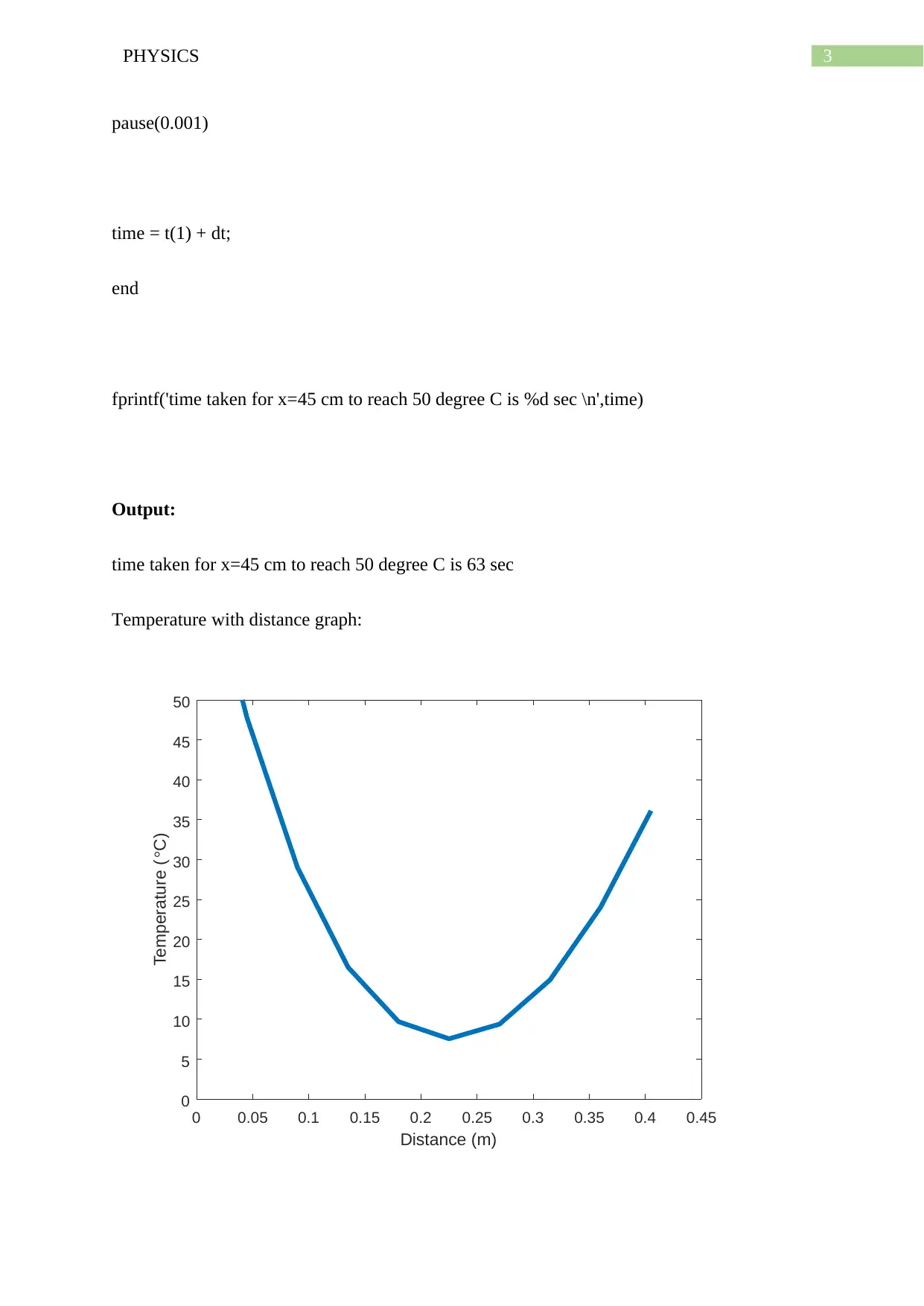
This assignment focuses on simulating heat diffusion using MATLAB. The student has provided MATLAB code to model the heat diffusion equation within a wall, considering parameters like wall thickness, thermal diffusivity, and boundary conditions. The code calculates the temperature distribution over time and distance, and the output includes a graph of temperature versus distance and the time taken for a specific point to reach a certain temperature. The assignment also includes the boundary conditions used in the simulation and references to relevant video resources on heat diffusion and MATLAB introduction. This practical exercise helps to understand and visualize the process of heat transfer and the application of numerical methods in solving physics problems.

Running head: Physics
PHYSICS
Name of the Student
Name of the University
Author Note

1PHYSICS
MATLAB code:
L = 0.45; %wall thickness
n = 10; %number of simulation nodes
T0 = 0; %deg C, initial temperature of wall
T1s = 100; %deg C, surface 1 temperature
Tx = 50; %deg C, distance x temperature
dx = L/n; %m, node thickness
alpha = 127*10^-6; %thermal diffusivity
t_final = 63; %s, simulation time
dt= 0.1; %s, fixed time step
x = 0:dx:L-dx/2;
T = ones(n,1)*T0;

2PHYSICS
dTdt = zeros(n,1);
t = 0:dt:t_final;
time = t(1);
for j = 1:length(t)
for i = 2:n-1
dTdt(i) = alpha*(-(T(i)-T(i-1))/dx^2+(T(i+1)-T(i))/dx^2);
end
dTdt(1)= alpha*(-(T(1)-T1s)/dx^2+(T(2)-T(1))/dx^2);
dTdt(n)= alpha*(-(T(n)-T(n-1))/dx^2+(Tx-T(n))/dx^2);
T = T+dTdt*dt;
if(x==0.45)AND(T==50)
Td=T;
break
end
figure(1)
plot(x,T, 'Linewidth', 3)
axis([0 L 0 50])
xlabel('Distance (m)')
ylabel('Temperature (\circC)')

3PHYSICS
pause(0.001)
time = t(1) + dt;
end
fprintf('time taken for x=45 cm to reach 50 degree C is %d sec \n',time)
Output:
time taken for x=45 cm to reach 50 degree C is 63 sec
Temperature with distance graph:
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45
Distance (m)
0
5
10
15
20
25
30
35
40
45
50
Temperature ( °C)

4PHYSICS
Boundary conditions:
Initial temperature is 0 degree C.
So, T(0) = 0 C for all x
At x= 0 T(0) = 100 degree C. (as temperature suddenly increased to 100 degree C)
Tend = 45 degree C.