University Physics: Wave and Vector Functions Homework Solution

This document presents a detailed solution to a physics assignment focused on wave and vector functions. The solution covers two scenarios, with the first involving the analysis of wave functions, including amplitude, phase, frequency, and periodic time calculations. It delves into finding maximum displacement, calculating time for specific displacements, and applying compound angle formulas to simplify wave equations. The second scenario addresses vector calculations, determining the slope length, and calculating the angle between vectors using the dot product. The assignment provides step-by-step solutions, demonstrating the application of key physics principles and mathematical techniques to solve complex problems related to wave and vector analysis.

Wave and Vector Functions

TABLE OF CONTENTS
SCENARIO 1...................................................................................................................................1
SCENARIO 2...................................................................................................................................5

SCENARIO 1
X1 ¿ 3.80 sin ¿ + ¿
9 ]
X2 = 4.62 sin [100π t - ( 2 π
5 )]
1.)
X1 ¿ 3.80 sin ¿ + ¿
9 ]
Amplitude: 3.80
Phase: 2 π
9 leading
Frequency: 50 Hz
Periodic time: 0.02 seconds
X2 = 4.62 sin [100π t - ( 2 π
5 )]
Amplitude: 4.62
Phase: - 2 π
5 lagging
Frequency: 50 Hz
Periodic time: 0.02 seconds
2.)
The maximum displacement can be found by differentiating x1 and x2 with respect to y.
X1 ¿ 3.80 sin ¿ + ¿
9 ]
d X 1
dt = 3.80* 100π cos [100π t + ¿
9 ]
For finding maximum displacement equate derivative to zero:
d X 1
dt = 0
100π t + ¿
9 = π
2
t1 = 0.0027 seconds
1

Similarly,
X2 = 4.62 sin [100π t - ( 2 π
5 )]
d X 2
dt = 4.62 * 100π cos [100π t - 2 π
5 ]
d X 1
dt = 0
100π t - 2 π
5 = π
2
t = 0.009 seconds
3 .)
When X1 = -2 mm time can be calculated as follows:
-2 = 3.80 sin [100π t + 2 π
9 ]
sin [100π t + 2 π
9 ] = -0.0052
[100π t + 2 π
9 ] = -0.553
t = 0.0039 seconds
CHECK
X1 = 3.80 sin [100π t + 2 π
9 ]
Putting t=0.0039
X1 = -2
Thus proved RHS = LHS
When X2 = -2
-2 = 4.62 Sin [100π t - 2 π
5 ]
t = 0.002 seconds
CHECK
2

X2= 4.62 Sin [100π t - 2 π
5 ]
Putting t=0.002
X2 = -2
Thus proved RHS = LHS
4.) Compound angle formula
X1 = 3.80 sin [100π t + 2 π
9 ]
Sin (A+B) = Sin A Cos B + Cos A Sin B
X1 =3.80 {[Sin 100πt * Cos 2 π
9 ] + [Cos 100πt * Sin 2 π
9 )]
X1= 2.91 Sin 100πt + 2.43 Cos 100πt
Thus, from the equation of X1:
A = 2.91 B= 2.43
CHECK
= 3.80 sin [100π t + 2 π
9 ] = 2.91 Sin 100πt + 2.43 Cos 100πt
RHS 2.91 Sin 100πt + 2.43 Cos 100πt
By using the identity A sin Ф +B cos Ф = R Sin (Ф- α) we get
R = √ (2.91 ² + 2.43 ²) = 3.80
tan α = 2.43/2.91 = 0.835
α = 2 π
9
so
2.91 Sin 100πt + 2.43 Cos 100πt = 3.80 sin [100π t + ( 2 π
9 )]
RHS = LHS
3

Similarly, for x2:
X2 = 4.62 sin [100π t - 2 π
5 ]
X2 =4.62 {[Sin 100πt * Cos −2 π
5 ]] - [Cos 100πt * Sin −2 π
5 ]
X2= 1.38 Sin 100πt + 4.38 Cos 100πt
Thus, from the equation of X1:
A = 1.38 B= 4.38
4.62 sin [100π t - 2 π
5 ] = 1.38 Sin 100πt + 4.38 Cos 100πt
CHECK
4.62 sin [100π t - 2 π
5 ] = 1.38 Sin 100πt + 4.38 Cos 100πt
By using the identity A sin Ф +B cos Ф = R Sin (Ф- α) we get
LHS:
1.38 Sin 100πt + 4.38 Cos 100πt
R = √ (1.38 ² + 4.38 ²) = 4.62
tan α = 4.38
1.38 = 3.17
α = 2π /5
1.38 Sin 100πt + 4.38 Cos 100πt =4.62 sin [100π t - ( 2 π
5 )]
Thus, LHS = RHS
5.)
From the above simplified expression x1 and x2 can be written as :
X1 = 2.91 Sin 100πt + 2.43 Cos 100πt
X2= 1.38 Sin 100πt + 4.38 Cos 100πt
X 1 +X 2 = 4.29 Sin 100πt + 6.81 Cos 100πt
4

The equation represents the form A sin Ф +B cos Ф
A = 4.29 B= 6.81
Tan α = b
a
So α = 57.67
R = √ (A ² + B²)
R = √ (4.29 ² + 6.81²)
R= 8.04
A sin Ф +B cos Ф = R Sin (Ф+ α)
8.04 Sin (100π t + 57.67)
CHECK
4.29 Sin 100πt + 6.81 Cos 100πt = 8.04 Sin (100π t + 57.67)
RHS
8.04 Sin (100π t + 57.67)
By using the identity Sin (A+B) = sin A cos B + cos A sin B
8.04 Sin (100π t + 57.67) = 8.04 [sin 100π t cos 57.67 + cos 100π t sin 57.67]
= 4.29 Sin 100πt + 6.81 Cos 100πt
Thus RHS = LHS
6.)
7.)
5

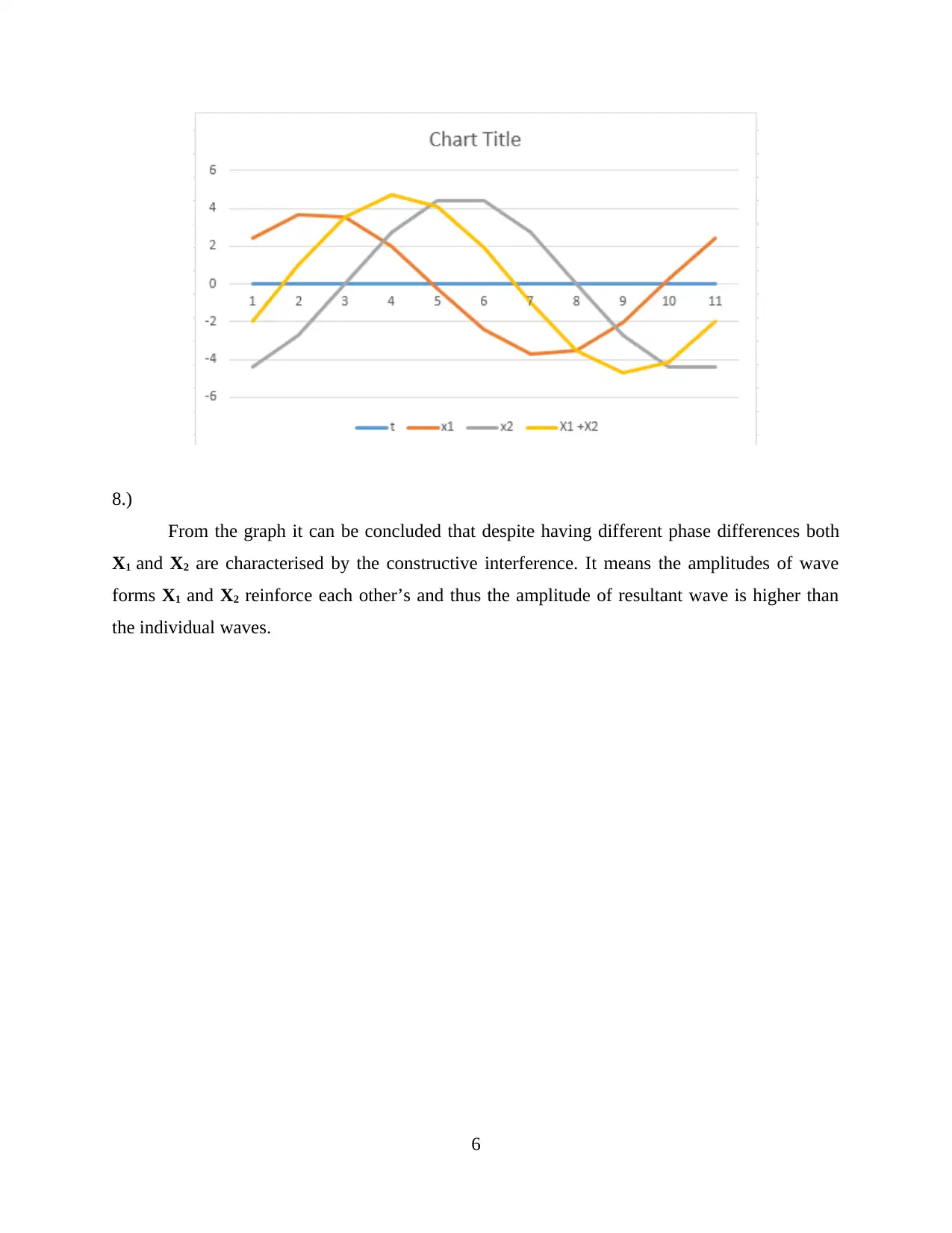
8.)
From the graph it can be concluded that despite having different phase differences both
X1 and X2 are characterised by the constructive interference. It means the amplitudes of wave
forms X1 and X2 reinforce each other’s and thus the amplitude of resultant wave is higher than
the individual waves.
6

SCENARIO 2
1.)
A = (0, -40, 0)
B = (40, 0, -20)
C = (a, b, 0)
Slope length AB = √ [(40)² + (40)² + (-20)²]
Slope length AB = 60
2.)
Lenght AB = B-A = (40, 40, -20)
BC is drilled in the direction of 3i +4j +k
Angle between AB and BC is given by the following formula:
Cos Ф = (AB.BC) / (magnitude AB*magnitude BC)
Cos Ф = (40*3 + 40*4 -20*1) / [√[(20)² + (20)² + (10)²] √ [(3)² + (4)² + (1)²]]
Cos Ф = 0.3333
Ф = 70.53 degree
7

3.)
vector C = vector B + rho (3i +4j+ k)
(a,b,0) = (40, 0, -20) + rho (3, 4 ,1)
rho = 20
A = 100
B= 80
8

9

10