Math Problem Solutions: Practical Applications and Step-by-Step Guide

This document provides solutions to a variety of practical math problems. It includes detailed solutions for problems involving inequalities, revenue and cost analysis, and functional graphs. The document also addresses calculus problems, including finding derivatives of different functions and determining slopes. Furthermore, it covers matrix operations and provides solutions for related problems. The solutions are presented with step-by-step explanations, making it a useful resource for students seeking to understand and solve math problems. This assignment is a valuable resource for anyone studying foundational math concepts, offering clear explanations and practical applications of mathematical principles. The solutions cover a range of topics, from basic algebra to calculus and matrix operations, making it a comprehensive guide for students.

Practical Question

Table of Contents
Question 1....................................................................................................................................1
Question 2....................................................................................................................................1
Question 3....................................................................................................................................1
Question 4....................................................................................................................................1
Question 5....................................................................................................................................2
Question 6....................................................................................................................................2
Question 7....................................................................................................................................2
QUESTION 8...............................................................................................................................2
QUESTION 9 ..............................................................................................................................3
Question 10..................................................................................................................................4
Question 11 .................................................................................................................................5
QUESTION 12.............................................................................................................................5
QUESTION 13.............................................................................................................................6
QUESTION 14 ............................................................................................................................6
QUESTION 15.............................................................................................................................7
QUESTION 16 ............................................................................................................................7

Question 1
The company monthly costs are $50 per unit (x), plus $1000 in overhead. The cost must
be more than 0 and less than $60,000. So, the inequality is as follows :-
0 < 50x + 1000 < 60,000
0 < 50x [phone] < 60,000 -1000
0 < 50x < 59000
0 < 50x < 59000
50 50
0 < x < 1180
Thus, company must produce goods in interval of 1180.
Question 2
The company revenue is 30 per unit (x). Its costs are 10 per unit (x) plus $400 overhead. So, the
inequality is :-
30x > 10x + 400
30x - 10x > 10x- 10x + 400
20x > 400
20x > 400
20 20
X > 20
Thus, company should produce more than 20 units to make profits.
Question 3
B and D are functional graphs.
Question 4
a) Quantity demanded at price $25 is 37.7
b) Domain of function is (0, 50)
c) Range of function is (0, 100)
1

Question 5
A.
f1(x) = -2x + 30
Number of DVD = 10 = x
So number of CD's produced = -2*10 +30 = 10
B.
f2(x) = -1.5x +30
f2(x= 10) = 15
C.
When 10 DVD's are produced
Slope of f1(x) = -2
Slope of f2(x) = -1.5
Thus, f1(x) is more stepper.
Question 6
A) x^2* X^0 = X^2
b) a^3b^2a^5b = a^8b^3
c) x^1/5y^6/5 = xy^6
z^2/5 z^2
d) ln e^ab + lne^3a= ab+3a
e) e^lnx^2= x^2
Question 7
In Y = ln2 + 1 lnK +1 lnL + 1 lnR
2 3 6
QUESTION 8
At maxima and minima point the slope is equals to zero. Thus, for the given function At
point B slope is zero.
2

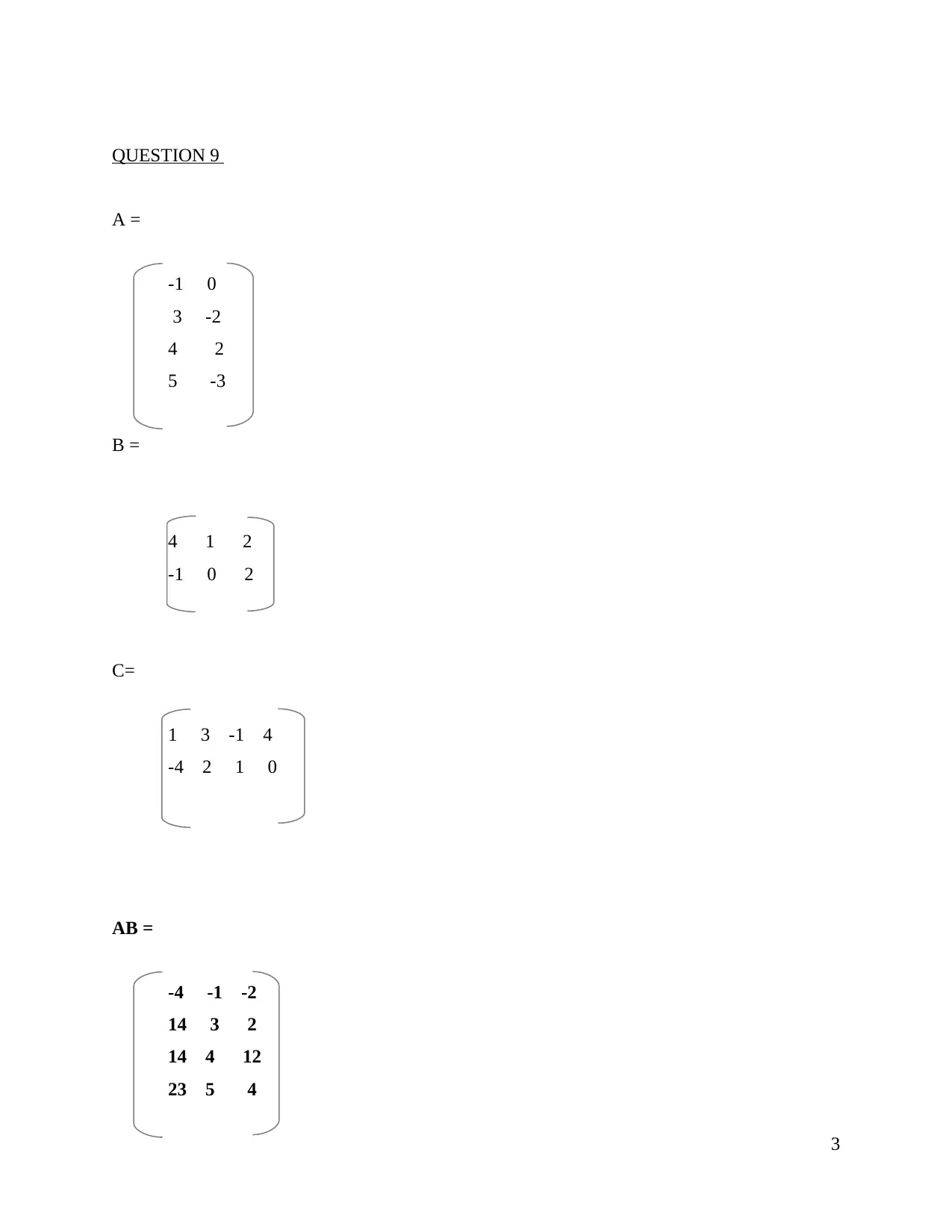
QUESTION 9
A =
-1 0
3 -2
4 2
5 -3
B =
4 1 2
-1 0 2
C=
1 3 -1 4
-4 2 1 0
AB =
-4 -1 -2
14 3 2
14 4 12
23 5 4
3

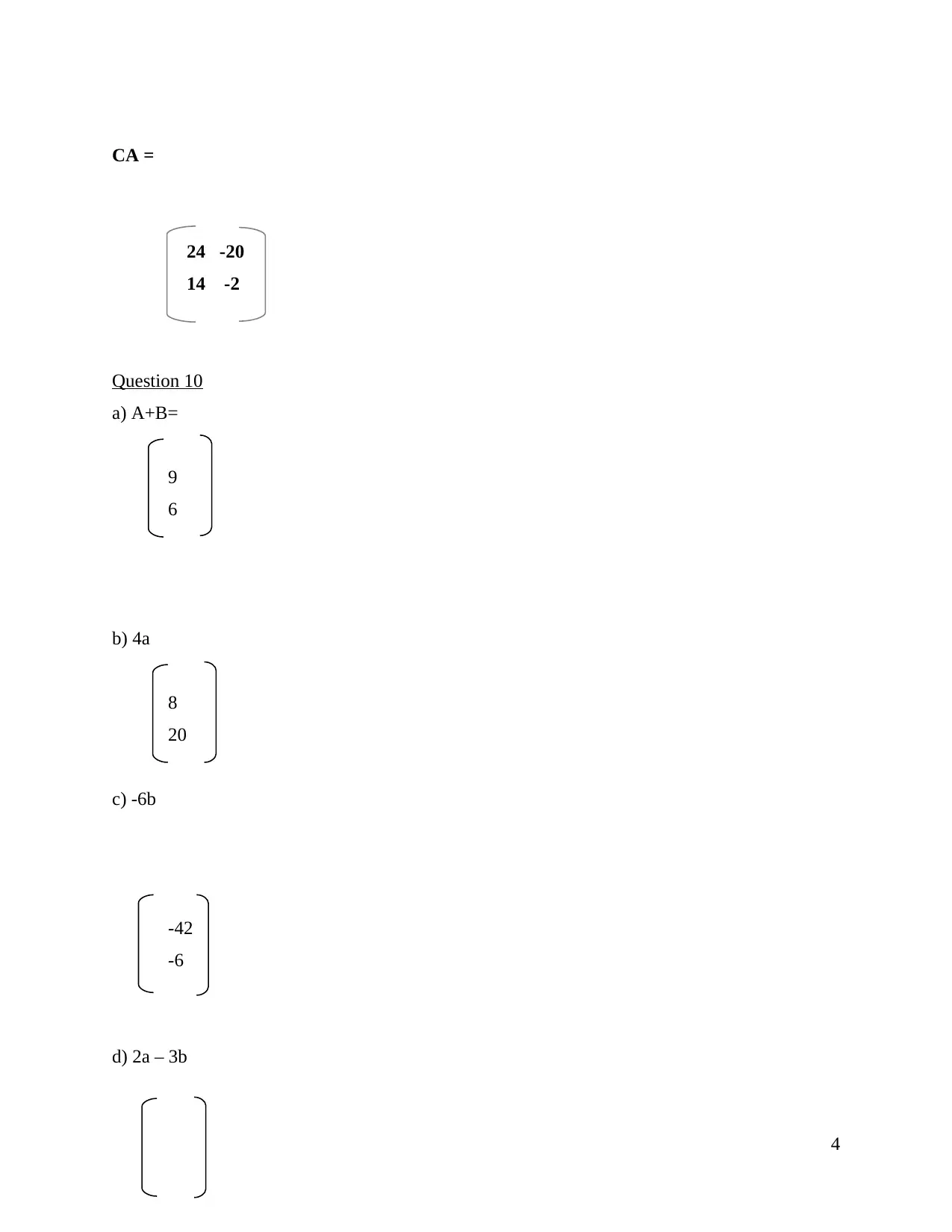
CA =
24 -20
14 -2
Question 10
a) A+B=
9
6
b) 4a
8
20
c) -6b
-42
-6
d) 2a – 3b
4

-17
7
Question 11
T h d c
10 15 9 12
20 14 8 5
16 8 15 6
25 15 7 16
5 12 20 18
QUESTION 12
Value of stock prior to the discount = V1 =
5000 4500 6000
10000 12000 7500
8000 9000 11000
V2 =
5000 4500 6000
10000 12000 7500 * 0.8
8000 9000 11000
4000 3600 4800
5

8000 9600 6000
6400 7200 8800
QUESTION 13
A.
y = [ (x^3) + 2 ] / (x – 1)
dy/dx = (x – 1)*{d([ (x^3) + 2 ])/dx} - [ (x^3) + 2 ]*{d(x – 1)/dx}
= { (3x^2) (x – 1) – 1* ([ (x^3) + 2 ]) } / (x – 1)^2
dy/dx = (2x^3 – 3x^2 – 2 ) / [(x -1)^2]
B.
y = e^{(4*x^2) + 3x – 1}
dy / dx = (8x + 3)* (e^{(4*x^2) + 3x – 1})
QUESTION 14
A.
y = (x + 7)*(2x +3)
dy/dx = (2x +3) [d(x +7)/dx] + (x +7) [d(2x +3)/dx]
= 2x + 3 + 2*(x + 7)
dy/dx = 4x +17
B.
y = (x^3 – 2x + 1)^ 15
dy/dx = (2x – 2)*15* [(x^3 – 2x + 1)^ 14 ]
C.
6

y = ln 3x +ln (5 + x^2)
dy /dx = (1/ ln 10) * [d(ln 3x) /dx]
dy/dx = 1/ln x
QUESTION 15
f(x) = 7x^2 – 9x + 3
Slope = dy/dx
dy/dx = 14x – 9
At x = 2
Slope = 19
QUESTION 16
f(x) = - 0.25x^2 + 36
x = coloured printer
f(x) = black and white printer
Rate of instantaneous change = df(x) / dx
df(x) / dx = -0.5x
When number of coloured printers is 10 then rate of change is given by
df(x = 10) / dx = -5
7

1

2